
Hardy field
Encyclopedia
In mathematics
, a Hardy field is a field
consisting of germs
of real-valued functions at infinity that is closed under differentiation
. They are named after the English mathematician G. H. Hardy
.
on H by saying f is equivalent to g if and only if f − g is eventually zero. The equivalence classes of this relation are called germs at infinity.
If H forms a field under the usual addition and multiplication of functions then so will H modulo this equivalence relation under the induced addition and multiplication operations. Moreover, if every function in H is eventually differentiable and the derivative of any function in H is also in H then H modulo the above equivalence relation is called a Hardy field.
Elements of a Hardy field are thus equivalence classes and should be denoted, say, [f]∞ to denote the class of functions that are eventually equal to the representative function f. However, in practice the elements are normally just denoted by the representatives themselves, so instead of [f]∞ one would just write f.
A less trivial example of a Hardy field is the field of rational function
s on R, denoted R(x). This is the set of functions of the form P(x)/Q(x) where P and Q are polynomials with real coefficients. Since the polynomial Q can have only finitely many zeros by the fundamental theorem of algebra
, such a rational function will be defined for all sufficiently large x, specifically for all x larger than the largest real root of Q. Adding and multiplying rational functions gives more rational functions, and the quotient rule shows that the derivative of rational function is again a rational function, so R(x) forms a Hardy field.
and eventually either have a multiplicative inverse or are zero. This means periodic functions such as the sine and cosine functions can't exist in Hardy fields.
This avoidance of periodic functions also means that every element in a Hardy field has a (possibly infinite) limit at infinity, so if f is an element of H, then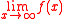
exists in R ∪ (−∞,+∞).
It also means we can place an ordering
on H by saying f < g if g − f is eventually strictly positive. Note that this is not the same as stating that f < g if the limit of f is less than the limit of g. For example if we consider the germs of the identity function f(x) = x and the exponential function g(x) = ex then since g(x) − f(x) > 0 for all x we have that g > f. But they both tend to infinity. In this sense the ordering tells us how quickly all the unbounded functions diverge to infinity.
s. Indeed, if R is an o-minimal
expansion of a field, then the set of unary definable functions in R that are defined for all sufficiently large elements forms a Hardy field denoted H(R). The properties of Hardy fields in the real setting still hold in this more general setting.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Hardy field is a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
consisting of germs
Germ (mathematics)
In mathematics, the notion of a germ of an object in/on a topological space captures the local properties of the object. In particular, the objects in question are mostly functions and subsets...
of real-valued functions at infinity that is closed under differentiation
Differentiation
Differentiation may refer to:* Differentiation , the process of finding a derivative* Differentiated instruction in education* Cellular differentiation in biology* Planetary differentiation in planetary science...
. They are named after the English mathematician G. H. Hardy
G. H. Hardy
Godfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
.
Definition
Initially at least, Hardy fields were defined in terms of germs of real functions at infinity. Specifically we consider a collection H of functions that are defined for all large real numbers, that is functions f that map (u,∞) to the real numbers R, where u is some real number depending on f. Here and in the rest of the article we say a function has a property "eventually" if it has the property for all sufficiently large x, so for example we say a function f in H is eventually zero if there is some real number U such that f(x) = 0 for all x ≥ U. We can form an equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on H by saying f is equivalent to g if and only if f − g is eventually zero. The equivalence classes of this relation are called germs at infinity.
If H forms a field under the usual addition and multiplication of functions then so will H modulo this equivalence relation under the induced addition and multiplication operations. Moreover, if every function in H is eventually differentiable and the derivative of any function in H is also in H then H modulo the above equivalence relation is called a Hardy field.
Elements of a Hardy field are thus equivalence classes and should be denoted, say, [f]∞ to denote the class of functions that are eventually equal to the representative function f. However, in practice the elements are normally just denoted by the representatives themselves, so instead of [f]∞ one would just write f.
Examples
If F is a subfield of R then we can consider it as a Hardy field by considering the elements of F as constant functions, that is by considering the number α in F as the constant function fα that maps every x in R to α. This is a field since F is, and since the derivative of every function in this field is 0 which must be in F it is a Hardy field.A less trivial example of a Hardy field is the field of rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s on R, denoted R(x). This is the set of functions of the form P(x)/Q(x) where P and Q are polynomials with real coefficients. Since the polynomial Q can have only finitely many zeros by the fundamental theorem of algebra
Fundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
, such a rational function will be defined for all sufficiently large x, specifically for all x larger than the largest real root of Q. Adding and multiplying rational functions gives more rational functions, and the quotient rule shows that the derivative of rational function is again a rational function, so R(x) forms a Hardy field.
Properties
Any element of a Hardy field is eventually either strictly positive, strictly negative, or zero. This follows fairly immediately from the facts that the elements in a Hardy field are eventually differentiable and hence continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
and eventually either have a multiplicative inverse or are zero. This means periodic functions such as the sine and cosine functions can't exist in Hardy fields.
This avoidance of periodic functions also means that every element in a Hardy field has a (possibly infinite) limit at infinity, so if f is an element of H, then
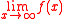
exists in R ∪ (−∞,+∞).
It also means we can place an ordering
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
on H by saying f < g if g − f is eventually strictly positive. Note that this is not the same as stating that f < g if the limit of f is less than the limit of g. For example if we consider the germs of the identity function f(x) = x and the exponential function g(x) = ex then since g(x) − f(x) > 0 for all x we have that g > f. But they both tend to infinity. In this sense the ordering tells us how quickly all the unbounded functions diverge to infinity.
In model theory
The modern theory of Hardy fields doesn't restrict to real functions but to those defined in certain structures expanding real closed fieldReal closed field
In mathematics, a real closed field is a field F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal numbers.-Definitions:...
s. Indeed, if R is an o-minimal
O-minimal theory
In mathematical logic, and more specifically in model theory, an infinite structure which is totally ordered by In mathematical logic, and more specifically in model theory, an infinite structure which is totally ordered by...
expansion of a field, then the set of unary definable functions in R that are defined for all sufficiently large elements forms a Hardy field denoted H(R). The properties of Hardy fields in the real setting still hold in this more general setting.

