Grothendieck inequality
Encyclopedia
In mathematics, the Grothendieck inequality states that there is a universal constant k with the following property. If ai,j is an n by n matrix
with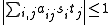
for all real number
s si, tj of absolute value at most 1, then
,
for all vectors Si, Tj in the unit ball B(H) of an n-dimensional Hilbert space
H. The smallest constant k which satisfies this property for all n by n matrices is called a Grothendieck constant and denoted k(n); in fact there are two Grothendieck constants kR(n) and kC(n) for each n depending on whether one works with real or complex Hilbert spaces, respectively.
The sequences kR(n) and kC(n) are easily seen to be increasing, and Alexander Grothendieck
's result states that they are bounded, so they have limits
.
If we define kR to be supn kR(n) then Grothendieck proved that: 1.57 ≤ kR ≤ 2.3.
Later Krivine improved the result by proving: 1.67696... ≤ kR ≤ 1.7822139781...=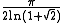
, conjecturing that the upper bound is tight. However, this conjecture was disproved in a preprint by Braverman, Makarychev, Makarychev and Naor.
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with
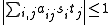
for all real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s si, tj of absolute value at most 1, then
,for all vectors Si, Tj in the unit ball B(H) of an n-dimensional Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
H. The smallest constant k which satisfies this property for all n by n matrices is called a Grothendieck constant and denoted k(n); in fact there are two Grothendieck constants kR(n) and kC(n) for each n depending on whether one works with real or complex Hilbert spaces, respectively.
The sequences kR(n) and kC(n) are easily seen to be increasing, and Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
's result states that they are bounded, so they have limits
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
.
If we define kR to be supn kR(n) then Grothendieck proved that: 1.57 ≤ kR ≤ 2.3.
Later Krivine improved the result by proving: 1.67696... ≤ kR ≤ 1.7822139781...=
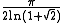, conjecturing that the upper bound is tight. However, this conjecture was disproved in a preprint by Braverman, Makarychev, Makarychev and Naor.