
Goursat's lemma
Encyclopedia
Goursat's lemma is an algebra
ic theorem
about subgroup
s of the direct product
of two groups
.
It can be stated as follows.
An immediate consequence of this is that the subdirect product of two groups can be described as a fiber product and vice versa.
,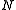 and
and 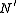 are shown to be normal in
are shown to be normal in 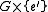 and
and 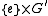 , respectively. It is in this sense that
, respectively. It is in this sense that 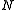 and
and 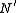 can be identified as normal in G and G, respectively.
can be identified as normal in G and G, respectively.
Since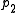 is a homomorphism
is a homomorphism
, its kernel N is normal in H. Moreover, given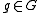 , there exists
, there exists 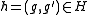 , since
, since 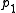 is surjective. Therefore,
is surjective. Therefore, 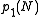 is normal in G, viz:
is normal in G, viz: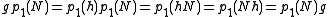 .
.
It follows that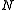 is normal in
is normal in 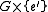 since
since
The proof that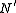 is normal in
is normal in 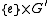 proceeds in a similar manner.
proceeds in a similar manner.
Given the identification of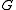 with
with 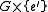 , we can write
, we can write 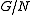 and
and 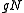 instead of
instead of 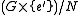 and
and 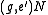 ,
, 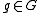 . Similarly, we can write
. Similarly, we can write 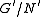 and
and 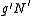 ,
, 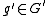 .
.
On to the proof. Consider the map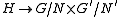 defined by
defined by 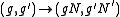 . The image of
. The image of 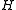 under this map is
under this map is 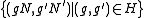 . This relation
. This relation
is the graph of a well-defined
function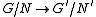 provided
provided 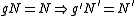 , essentially an application of the vertical line test
, essentially an application of the vertical line test
.
Since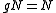 (more properly,
(more properly, 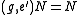 ), we have
), we have 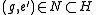 . Thus
. Thus 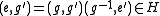 , whence
, whence 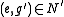 , that is,
, that is, 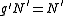 . Note that by symmetry, it is immediately clear that
. Note that by symmetry, it is immediately clear that 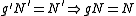 , i.e., this function also passes the horizontal line test
, i.e., this function also passes the horizontal line test
, and is therefore one-to-one
. The fact that this function is a surjective group homomorphism follows directly.
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
ic theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
about subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s of the direct product
Direct product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
of two groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
.
It can be stated as follows.
- Let
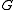 ,
, 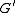 be groups, and let
be groups, and let 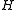 be a subgroup of
be a subgroup of 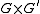 such that the two projectionsProjection (mathematics)Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...
such that the two projectionsProjection (mathematics)Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...
 and
and 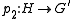 are surjective (i.e.,
are surjective (i.e., 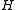 is a subdirect productSubdirect productIn mathematics, especially in the areas of abstract algebra known as universal algebra, group theory, ring theory, and module theory, a subdirect product is a subalgebra of a direct product that depends fully on all its factors without however necessarily being the whole direct product...
is a subdirect productSubdirect productIn mathematics, especially in the areas of abstract algebra known as universal algebra, group theory, ring theory, and module theory, a subdirect product is a subalgebra of a direct product that depends fully on all its factors without however necessarily being the whole direct product...
of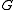 and
and 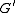 ). Let
). Let 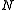 be the kernel of
be the kernel of  and
and 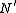 the kernelKernel (mathematics)In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
the kernelKernel (mathematics)In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
of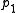 . One can identify
. One can identify 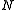 as a normal subgroupNormal subgroupIn abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
as a normal subgroupNormal subgroupIn abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of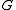 , and
, and 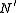 as a normal subgroup of
as a normal subgroup of 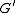 . Then the image of
. Then the image of  in
in 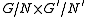 is the graphGraph of a functionIn mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
is the graphGraph of a functionIn mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
of an isomorphismIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
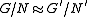 .
.
An immediate consequence of this is that the subdirect product of two groups can be described as a fiber product and vice versa.
Proof of Goursat's Lemma
Before proceeding with the proofMathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
,
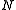 and
and 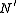 are shown to be normal in
are shown to be normal in 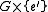 and
and 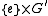 , respectively. It is in this sense that
, respectively. It is in this sense that 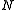 and
and 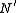 can be identified as normal in G and G, respectively.
can be identified as normal in G and G, respectively.Since
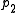 is a homomorphism
is a homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
, its kernel N is normal in H. Moreover, given
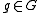 , there exists
, there exists 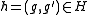 , since
, since 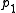 is surjective. Therefore,
is surjective. Therefore, 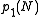 is normal in G, viz:
is normal in G, viz: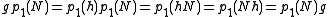 .
.It follows that
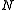 is normal in
is normal in 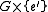 since
since
-
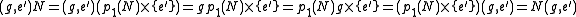 .
.
The proof that
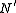 is normal in
is normal in 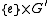 proceeds in a similar manner.
proceeds in a similar manner.Given the identification of
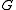 with
with 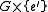 , we can write
, we can write 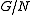 and
and 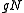 instead of
instead of 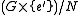 and
and 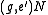 ,
, 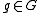 . Similarly, we can write
. Similarly, we can write 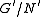 and
and 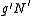 ,
, 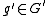 .
.On to the proof. Consider the map
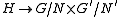 defined by
defined by 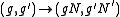 . The image of
. The image of 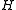 under this map is
under this map is 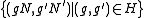 . This relation
. This relationRelation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
is the graph of a well-defined
Well-defined
In mathematics, well-definition is a mathematical or logical definition of a certain concept or object which uses a set of base axioms in an entirely unambiguous way and satisfies the properties it is required to satisfy. Usually definitions are stated unambiguously, and it is clear they satisfy...
function
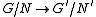 provided
provided 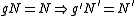 , essentially an application of the vertical line test
, essentially an application of the vertical line testVertical line test
In mathematics, the vertical line test is a test to determine if a curve is a relation or graph of a function when the function's domain and Range correspond to the x and y axes of the Cartesian coordinate system...
.
Since
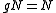 (more properly,
(more properly, 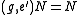 ), we have
), we have 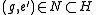 . Thus
. Thus 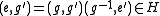 , whence
, whence 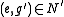 , that is,
, that is, 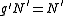 . Note that by symmetry, it is immediately clear that
. Note that by symmetry, it is immediately clear that 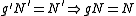 , i.e., this function also passes the horizontal line test
, i.e., this function also passes the horizontal line testHorizontal line test
In mathematics, the horizontal line test is a test used to determine if a function is injective and/or surjective.The lines used for the test are parallel to the x axis....
, and is therefore one-to-one
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
. The fact that this function is a surjective group homomorphism follows directly.

