Geometric integrator
Encyclopedia
In the mathematical field of numerical ordinary differential equations
, a geometric integrator is a numerical method that preserves geometric properties of the exact flow of a differential equation.
Assume that we have a pendulum whose bob has mass and
and
whose rod is massless of length . Take the
. Take the
acceleration due to gravity to be . Denote by
. Denote by
 the angular displacement of the rod from the vertical,
the angular displacement of the rod from the vertical,
and by the pendulum's momentum. The Hamiltonian
the pendulum's momentum. The Hamiltonian
of
the system, the sum of its kinetic
and potential
energies, is

which gives Hamilton's equations

It is natural to take the configuration space
 of all
of all  to be the unit
to be the unit
circle , so that
, so that  lies on the
lies on the
cylinder . However, we will take
. However, we will take
 , simply because
, simply because  -space is
-space is
then easier to plot. Define
and . Let us experiment by
. Let us experiment by
using some simple numerical methods to integrate this system. As usual,
we select a constant step size, , and for an aribtrary non-negative integer
, and for an aribtrary non-negative integer  we write
we write
 .
.
We use the following methods.
(explicit Euler),
(implicit Euler),
(Note that the symplectic Euler method treats q by the explicit and by the implicit Euler method.)
by the implicit Euler method.)
The observation that is constant along the solution
is constant along the solution
curves of the Hamilton's equations allows us to describe the exact
trajectories of the system: they are the level curves
of . We plot, in
. We plot, in  , the exact
, the exact
trajectories and the numerical solutions of the system. For the explicit
and implicit Euler methods we take , and z0 = (0.5, 0) and (1.5, 0) respectively; for the other two methods we take
, and z0 = (0.5, 0) and (1.5, 0) respectively; for the other two methods we take  , and z0 = (0, 0.7), (0, 1.4) and (0, 2.1).
, and z0 = (0, 0.7), (0, 1.4) and (0, 2.1).
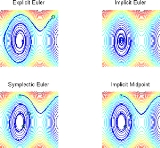
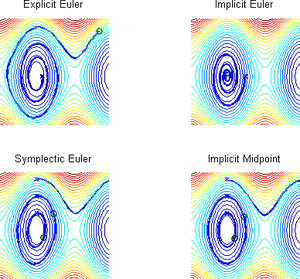 The explicit (resp. implicit) Euler method spirals out from (resp. in to) the origin. The other two methods show the correct qualitative behaviour, with the implicit midpoint rule agreeing with the exact solution to a greater degree than the symplectic Euler method.
The explicit (resp. implicit) Euler method spirals out from (resp. in to) the origin. The other two methods show the correct qualitative behaviour, with the implicit midpoint rule agreeing with the exact solution to a greater degree than the symplectic Euler method.
Recall that the exact flow of a Hamiltonian system with one degree of freedom is
of a Hamiltonian system with one degree of freedom is
area-preserving, in the sense that for all
for all  .
.
This formula is easily verified by hand. For our pendulum
example we see that the numerical flow of the explicit Euler method is not area-preserving; viz.,
of the explicit Euler method is not area-preserving; viz.,

A similar calculation can be carried out for the implicit Euler method,
where the determinant is

However, the symplectic Euler method is area-preserving:

thus . The implicit midpoint rule has similar geometric properties.
. The implicit midpoint rule has similar geometric properties.
To summarize: the pendulum example shows that, besides the explicit and
implicit Euler methods not being good choices of method to solve the
problem, the symplectic Euler method and implicit midpoint rule agree
well with the exact flow of the system, with the midpoint rule agreeing
more closely. Furthermore, these latter two methods are area-preserving,
just as the exact flow is; they are two examples of geometric (in fact, symplectic
) integrators.
method can be used to construct numerical methods which preserve Lie
symmetries
of the ODE. Existing methods such as Runge-Kutta can be modified using moving frame method to produce invariant versions.
Numerical ordinary differential equations
Numerical ordinary differential equations is the part of numerical analysis which studies the numerical solution of ordinary differential equations...
, a geometric integrator is a numerical method that preserves geometric properties of the exact flow of a differential equation.
Pendulum example
We can motivate the study of geometric integrators by considering the motion of a pendulum.Assume that we have a pendulum whose bob has mass
 and
andwhose rod is massless of length
 . Take the
. Take theacceleration due to gravity to be
 . Denote by
. Denote by the angular displacement of the rod from the vertical,
the angular displacement of the rod from the vertical,and by
 the pendulum's momentum. The Hamiltonian
the pendulum's momentum. The HamiltonianHamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
of
the system, the sum of its kinetic
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
and potential
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
energies, is

which gives Hamilton's equations

It is natural to take the configuration space
Configuration space
- Configuration space in physics :In classical mechanics, the configuration space is the space of possible positions that a physical system may attain, possibly subject to external constraints...
 of all
of all  to be the unit
to be the unitcircle
 , so that
, so that  lies on the
lies on thecylinder
 . However, we will take
. However, we will take , simply because
, simply because  -space is
-space isthen easier to plot. Define

and
 . Let us experiment by
. Let us experiment byusing some simple numerical methods to integrate this system. As usual,
we select a constant step size,
 , and for an aribtrary non-negative integer
, and for an aribtrary non-negative integer  we write
we write .
.We use the following methods.
(explicit Euler),
(implicit Euler),
-
 (symplectic Euler),
(symplectic Euler),
-
 (implicit midpoint rule).
(implicit midpoint rule).
(Note that the symplectic Euler method treats q by the explicit and
 by the implicit Euler method.)
by the implicit Euler method.)The observation that
 is constant along the solution
is constant along the solutioncurves of the Hamilton's equations allows us to describe the exact
trajectories of the system: they are the level curves
Level set
In mathematics, a level set of a real-valued function f of n variables is a set of the formthat is, a set where the function takes on a given constant value c....
of
 . We plot, in
. We plot, in  , the exact
, the exacttrajectories and the numerical solutions of the system. For the explicit
and implicit Euler methods we take
 , and z0 = (0.5, 0) and (1.5, 0) respectively; for the other two methods we take
, and z0 = (0.5, 0) and (1.5, 0) respectively; for the other two methods we take  , and z0 = (0, 0.7), (0, 1.4) and (0, 2.1).
, and z0 = (0, 0.7), (0, 1.4) and (0, 2.1).
Recall that the exact flow
 of a Hamiltonian system with one degree of freedom is
of a Hamiltonian system with one degree of freedom isarea-preserving, in the sense that
 for all
for all  .
.This formula is easily verified by hand. For our pendulum
example we see that the numerical flow
 of the explicit Euler method is not area-preserving; viz.,
of the explicit Euler method is not area-preserving; viz.,
A similar calculation can be carried out for the implicit Euler method,
where the determinant is

However, the symplectic Euler method is area-preserving:

thus
 . The implicit midpoint rule has similar geometric properties.
. The implicit midpoint rule has similar geometric properties.To summarize: the pendulum example shows that, besides the explicit and
implicit Euler methods not being good choices of method to solve the
problem, the symplectic Euler method and implicit midpoint rule agree
well with the exact flow of the system, with the midpoint rule agreeing
more closely. Furthermore, these latter two methods are area-preserving,
just as the exact flow is; they are two examples of geometric (in fact, symplectic
Symplectic integrator
In mathematics, a symplectic integrator is a numerical integration scheme for a specific group of differential equations related to classical mechanics and symplectic geometry. Symplectic integrators form the subclass of geometric integrators which, by definition, are canonical transformations...
) integrators.
Moving frame method
The moving frameMoving frame
In mathematics, a moving frame is a flexible generalization of the notion of an ordered basis of a vector space often used to study the extrinsic differential geometry of smooth manifolds embedded in a homogeneous space.-Introduction:...
method can be used to construct numerical methods which preserve Lie
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
symmetries
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of the ODE. Existing methods such as Runge-Kutta can be modified using moving frame method to produce invariant versions.



