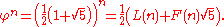Generalizations of Fibonacci numbers
Encyclopedia
In mathematics
, the Fibonacci number
s form a sequence
defined recursively
by:
That is, after two starting values, each number is the sum of the two preceding numbers.
The Fibonacci sequence has been studied extensively and generalized in many ways, for example, by starting with other numbers than 0 and 1, by adding more than two numbers to generate the next number, or by adding objects other than numbers.
See also Negafibonacci.
φ, and are based on Binet's formula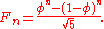
The analytic function
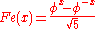
has the property that Fe(n) = Fn for even integers n. Similarly, the analytic function:
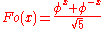
satisfies Fo(n) = Fn for odd integers n.
Finally, putting these together, the analytic function
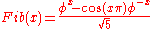
satisfies Fib(n)=Fn for all integers n.
This formula can be used to compute the generalized Fibonacci function of a complex variable. For example,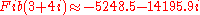
g from the integers to a field for which g(n+2) = g(n) + g(n+1). These functions are precisely those of the form g(n) = F(n)g(1) + F(n-1)g(0), so the Fibonacci sequences form a vector space
with the functions F(n) and F(n-1) as a basis.
More generally, the range of g may be taken to be any abelian group
(regarded as a Z-module
). Then the Fibonacci sequences form a 2-dimensional Z-module in the same way.
where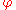 is the golden ratio.
is the golden ratio.
Written in the form

a = 0 if and only if b = 0.
Thus the ratio between two consecutive elements converges to the golden ratio, except in the case of the sequence which is constantly zero.
Written in this form the simplest non-trivial example (a = b = 1) is the sequence of Lucas number
s:

We have L(1) = 1 and L(2) = 3. The properties include:
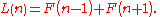
See also Fibonacci integer sequences modulo n.
s of the kind defined as follows:
where the normal Fibonacci sequence is the special case of P = 1 and Q = −1. Another kind of Lucas sequence begins with V(0) = 2, V(1) = P. Such sequences have applications in number theory and primality
proving.
of nonnegative integers into parts that are at most n is a Fibonacci sequence of order n. The sequence of the number of strings of 0s and 1s of length m that contain at most n consecutive 0s is also a Fibonacci sequence of order n.
The tribonacci constant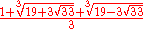 is the ratio toward which adjacent tribonacci numbers tend. It is a root of the polynomial x3 − x2 − x − 1, approximately 1.83929 , and also satisfies the equation x + x−3 = 2. It is important in the study of the snub cube
is the ratio toward which adjacent tribonacci numbers tend. It is a root of the polynomial x3 − x2 − x − 1, approximately 1.83929 , and also satisfies the equation x + x−3 = 2. It is important in the study of the snub cube
.
The tribonacci numbers are also given by
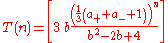
where the outer brackets denote the nearest integer function
and

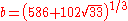 .
.
The tetranacci constant is the ratio toward which adjacent tetranacci numbers tend. It is a root of the polynomial x4 − x3 − x2 − x − 1, approximately 1.92756, and also satisfies the equation x + x−4 = 2.
Hexanacci numbers:
Heptanacci numbers:
The limit of the ratio of successive terms of an n-nacci series tends to a root of the equation
An alternate recursive formula for the limit of ratio r of two consecutive n-nacci numbers can be expressed as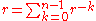 .
.
The special case n=2 is the traditional Fibonacci series yielding the gold section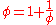 .
.
The above formulas for the ratio hold even for n-nacci series generated from arbitrary numbers.
The limit of this ratio is 2 as n increases. A 'polynacci' sequence, if one could be described, would after an infinite number of zeroes yield the sequence
which are simply powers of 2.
And the kth element of the n-nacci sequence is given by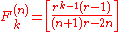
where the outer brackets denote the nearest integer function and r is the n-nacci constant which is the root of near to 2.
near to 2.
A Coin Tossing Problem is related to the n-nacci sequence. The probability that no n consecutive tails will occur in m tosses of an idealized coin is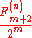 .
.
is defined by: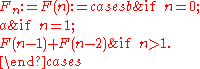
where + denotes the concatenation of two strings. The sequence of Fibonacci strings starts:
The length of each Fibonacci string is a Fibonacci number, and similarly there exists a corresponding Fibonacci string for each Fibonacci number.
Fibonacci strings appear as inputs for the worst case
in some computer algorithms.
If "a" and "b" represent two different materials or atomic bond lengths, the structure corresponding to a Fibonacci string is a Fibonacci quasicrystal
, an aperiodic quasicrystal
structure with unusual spectral
properties.
The Padovan sequence
is generated by the recurrence P(n) = P(n − 2) + P(n − 3).
A random Fibonacci sequence can be defined by tossing a coin for each position n of the sequence and taking F(n)=F(n−1)+F(n−2) if it lands heads and F(n)=F(n−1)−F(n−2) if it lands tails. Work by Furstenburg and Kesten guarantees that this sequence almost surely
grows exponentially at a constant rate: the constant is independent of the coin tosses and was computed in 1999 by Divakar Viswanath. It is now known as Viswanath's constant
.
A repfigit, or Keith number, is an integer such that, when its digits start a Fibonacci sequence with that number of digits, the original number is eventually reached. An example is 47, because the Fibonacci sequence starting with 4 and 7 (4,7,11,18,29,47) reaches 47. A repfigit can be a tribonacci sequence if there are 3 digits in the number, a tetranacci number if the number has four digits, etc. The first few repfigits are:
Since the set of sequences satisfying the relation S(n) = S(n−1) + S(n−2) is closed under termwise addition and under termwise multiplication by a constant, it can be viewed as a vector space
. Any such sequence is uniquely determined by a choice of two elements, so the vector space is two-dimensional. If we abbreviate such a sequence as (S(0), S(1)), the Fibonacci sequence F(n) = (0, 1) and the shifted Fibonacci sequence F(n−1) = (1, 0) are seen to form a canonical basis for this space, yielding the identity:
for all such sequences S. For example, if S is the Lucas sequence 2, 1, 3, 4, 7, 11…, then we obtain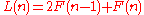 .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Fibonacci number
Fibonacci number
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
s form a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
defined recursively
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
by:
- F(0) = 0
- F(1) = 1
- F(n) = F(n-1) + F(n-2), for integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
n > 1.
That is, after two starting values, each number is the sum of the two preceding numbers.
The Fibonacci sequence has been studied extensively and generalized in many ways, for example, by starting with other numbers than 0 and 1, by adding more than two numbers to generate the next number, or by adding objects other than numbers.
Extension to negative integers
Using Fn-2 = Fn - Fn-1, one can extend the Fibonacci numbers to negative integers. So we get: ... -8, 5, -3, 2, -1, 1, 0, 1, 1, 2, 3, 5, 8, ... and F-n = -(-1)nFn.See also Negafibonacci.
Extension to all real or complex numbers
There are a number of possible generalizations of the Fibonacci numbers which include the real numbers (and sometimes the complex numbers) in their domain. These each involve the golden ratioGolden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
φ, and are based on Binet's formula
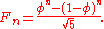
The analytic function
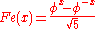
has the property that Fe(n) = Fn for even integers n. Similarly, the analytic function:
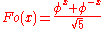
satisfies Fo(n) = Fn for odd integers n.
Finally, putting these together, the analytic function
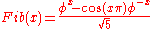
satisfies Fib(n)=Fn for all integers n.
This formula can be used to compute the generalized Fibonacci function of a complex variable. For example,
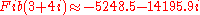
Vector space
The term Fibonacci sequence is also applied more generally to any functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
g from the integers to a field for which g(n+2) = g(n) + g(n+1). These functions are precisely those of the form g(n) = F(n)g(1) + F(n-1)g(0), so the Fibonacci sequences form a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
with the functions F(n) and F(n-1) as a basis.
More generally, the range of g may be taken to be any abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
(regarded as a Z-module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
). Then the Fibonacci sequences form a 2-dimensional Z-module in the same way.
Fibonacci integer sequences
The 2-dimensional Z-module of Fibonacci integer sequences consists of all integer sequences satisfying g(n+2) = g(n) + g(n+1). Expressed in terms of two initial values we have:- g(n) = F(n)g(1) + F(n-1)g(0) =

where
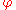 is the golden ratio.
is the golden ratio.Written in the form

a = 0 if and only if b = 0.
Thus the ratio between two consecutive elements converges to the golden ratio, except in the case of the sequence which is constantly zero.
Written in this form the simplest non-trivial example (a = b = 1) is the sequence of Lucas number
Lucas number
The Lucas numbers are an integer sequence named after the mathematician François Édouard Anatole Lucas , who studied both that sequence and the closely related Fibonacci numbers...
s:

We have L(1) = 1 and L(2) = 3. The properties include:
See also Fibonacci integer sequences modulo n.
Lucas sequences
A generalization of the Fibonacci sequence are the Lucas sequenceLucas sequence
In mathematics, the Lucas sequences Un and Vn are certain integer sequences that satisfy the recurrence relationwhere P and Q are fixed integers...
s of the kind defined as follows:
- U(0) = 0
- U(1) = 1
- U(n + 2) = PU(n + 1) − QU(n)
where the normal Fibonacci sequence is the special case of P = 1 and Q = −1. Another kind of Lucas sequence begins with V(0) = 2, V(1) = P. Such sequences have applications in number theory and primality
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
proving.
Fibonacci numbers of higher order
A Fibonacci sequence of order n is an integer sequence in which each sequence element is the sum of the previous n elements (with the exception of the first n elements in the sequence). The usual Fibonacci numbers are a Fibonacci sequence of order 2. The cases n=3 and n=4 have been thoroughly investigated. The number of compositionsComposition (number theory)
In mathematics, a composition of an integer n is a way of writing n as the sum of a sequence of positive integers. Two sequences that differ in the order of their terms define different compositions of their sum, while they are considered to define the same partition of that number. Any integer...
of nonnegative integers into parts that are at most n is a Fibonacci sequence of order n. The sequence of the number of strings of 0s and 1s of length m that contain at most n consecutive 0s is also a Fibonacci sequence of order n.
Tribonacci numbers
The tribonacci numbers are like the Fibonacci numbers, but instead of starting with two predetermined terms, the sequence starts with three predetermined terms and each term afterwards is the sum of the preceding three terms. The first few tribonacci numbers are:- 00 (number)0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
, 00 (number)0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
, 1, 1, 2, 4, 7, 1313 (number)13 is the natural number after 12 and before 14. It is the smallest number with eight letters in its name spelled out in English. It is also the first of the teens – the numbers 13 through 19 – the ages of teenagers....
, 2424 (number)24 is the natural number following 23 and preceding 25.The SI prefix for 1024 is yotta , and for 10−24 yocto...
, 4444 (number)44 is the natural number following 43 and preceding 45.- In mathematics :Forty-four is a tribonacci number, a happy number, an octahedral number and a palindromic number....
, 8181 (number)81 is the natural number following 80 and preceding 82.-In mathematics:Eighty-one is the square of 9 and the fourth power of 3. Like all powers of three, 81 is a perfect totient number. It is a heptagonal number and a centered octagonal number. It is also a tribonacci number, and an open meandric...
, 149149 (number)149 is the natural number between 148 and 150. It is also a prime number.-In mathematics:*149 is the 35th prime number, and with the next prime number, 151, is a twin prime, thus 149 is a Chen prime. 149 is a strong prime in the sense that it is more than the arithmetic mean of its two neighboring...
, 274, 504, 927, 1705, 3136, 5768, 10609, 19513, 35890, 66012, …
The tribonacci constant
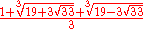 is the ratio toward which adjacent tribonacci numbers tend. It is a root of the polynomial x3 − x2 − x − 1, approximately 1.83929 , and also satisfies the equation x + x−3 = 2. It is important in the study of the snub cube
is the ratio toward which adjacent tribonacci numbers tend. It is a root of the polynomial x3 − x2 − x − 1, approximately 1.83929 , and also satisfies the equation x + x−3 = 2. It is important in the study of the snub cubeSnub cube
In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid.The snub cube has 38 faces, 6 of which are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron, that is, it has two distinct forms, which are mirror images of each...
.
The tribonacci numbers are also given by
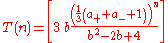
where the outer brackets denote the nearest integer function
Nearest integer function
In computer science, the nearest integer function of real number x denoted variously by [x], \lfloor x \rceil, \Vert x \Vert, nint, or Round, is a function which returns the nearest integer to x. To avoid ambiguity when operating on half-integers, a rounding rule must be chosen...
and

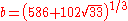 .
.Tetranacci numbers
The tetranacci numbers start with four predetermined terms, each term afterwards being the sum of the preceding four terms. The first few tetranacci numbers are:- 0, 0, 0, 1, 1, 2, 4, 8, 1515 (number)15 is the natural number following 14 and preceding 16. In English, it is the smallest natural number with seven letters in its spelled name....
, 2929 (number)29 is the natural number following 28 and preceding 30.-In mathematics:It is the tenth prime number, and also the fourth primorial prime. It forms a twin prime pair with thirty-one, which is also a primorial prime. Twenty-nine is also the sixth Sophie Germain prime. It is also the sum of three...
, 5656 (number)56 is the natural number following 55 and preceding 57.- Mathematics :56 is the sum of the first six triangular numbers , as well as the sum of six consecutive primes . It is also a tetranacci number and a pronic number. Adding up the divisors of 1 through 8 gives 56...
, 108108 (number)108 is the natural number following 107 and preceding 109.- In mathematics :One hundred [and] eight is an abundant number and a semiperfect number...
, 208, 401, 773, 1490, 2872, 5536, 10671, 20569, 39648, 76424, 147312, 283953, 547337, …
The tetranacci constant is the ratio toward which adjacent tetranacci numbers tend. It is a root of the polynomial x4 − x3 − x2 − x − 1, approximately 1.92756, and also satisfies the equation x + x−4 = 2.
Higher orders
Pentanacci, hexanacci, and heptanacci numbers have been computed. The pentanacci numbers are:- 0, 0, 0, 0, 1, 1, 2, 4, 8, 16, 31, 61, 120, 236, 464, 912, 1793, 3525, 6930, 13624, …
Hexanacci numbers:
- 0, 0, 0, 0, 0, 1, 1, 2, 4, 8, 16, 32, 63, 125, 248, 492, 976, 1936, 3840, 7617, 15109, …
Heptanacci numbers:
- 0, 0, 0, 0, 0, 0, 1, 1, 2, 4, 8, 16, 32, 64, 127, 253, 504, 1004, 2000, 3984, 7936, 15808, …
The limit of the ratio of successive terms of an n-nacci series tends to a root of the equation

An alternate recursive formula for the limit of ratio r of two consecutive n-nacci numbers can be expressed as
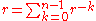 .
.The special case n=2 is the traditional Fibonacci series yielding the gold section
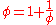 .
.The above formulas for the ratio hold even for n-nacci series generated from arbitrary numbers.
The limit of this ratio is 2 as n increases. A 'polynacci' sequence, if one could be described, would after an infinite number of zeroes yield the sequence
- [..., 0, 0, 1,] 1, 2, 4, 8, 16, 32, …
which are simply powers of 2.
And the kth element of the n-nacci sequence is given by
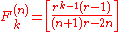
where the outer brackets denote the nearest integer function and r is the n-nacci constant which is the root of
 near to 2.
near to 2.A Coin Tossing Problem is related to the n-nacci sequence. The probability that no n consecutive tails will occur in m tosses of an idealized coin is
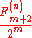 .
. Fibonacci word
In analogy to its numerical counterpart, the Fibonacci wordFibonacci word
thumb|350px|Characterization by a [[cutting sequence]] with a line of slope 1/\varphi or \varphi-1, with \varphi the [[golden ratio]].A Fibonacci word is a specific sequence of binary digits...
is defined by:
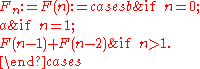
where + denotes the concatenation of two strings. The sequence of Fibonacci strings starts:
- b, a, ab, aba, abaab, abaababa, abaababaabaab, …
The length of each Fibonacci string is a Fibonacci number, and similarly there exists a corresponding Fibonacci string for each Fibonacci number.
Fibonacci strings appear as inputs for the worst case
Worst Case
Worst Case is the 3rd book in the Michael Bennett series from James Patterson and Michael Ledwidge.-Plot summary:NYPD Detective Mike Bennett and his new partner FBI Special Agent Emily Parker are on the trail of Francis Mooney, a Manhattan trusts and estates lawyer with terminal lung cancer...
in some computer algorithms.
If "a" and "b" represent two different materials or atomic bond lengths, the structure corresponding to a Fibonacci string is a Fibonacci quasicrystal
Fibonacci quasicrystal
The Fibonacci sequence is a type of quasicrystal in 1-dimension. A quasicrystal is a perfectly ordered material that never repeats the basic structural pattern, and these were discovered by 2011 Nobel Laureate Dan Shechtman.-Explanation:...
, an aperiodic quasicrystal
Quasicrystal
A quasiperiodic crystal, or, in short, quasicrystal, is a structure that is ordered but not periodic. A quasicrystalline pattern can continuously fill all available space, but it lacks translational symmetry...
structure with unusual spectral
Spectrum (functional analysis)
In functional analysis, the concept of the spectrum of a bounded operator is a generalisation of the concept of eigenvalues for matrices. Specifically, a complex number λ is said to be in the spectrum of a bounded linear operator T if λI − T is not invertible, where I is the...
properties.
Other generalizations
The Fibonacci polynomials are another generalization of Fibonacci numbers.The Padovan sequence
Padovan sequence
The Padovan sequence is the sequence of integers P defined by the initial valuesP=P=P=1,and the recurrence relationP=P+P.The first few values of P are...
is generated by the recurrence P(n) = P(n − 2) + P(n − 3).
A random Fibonacci sequence can be defined by tossing a coin for each position n of the sequence and taking F(n)=F(n−1)+F(n−2) if it lands heads and F(n)=F(n−1)−F(n−2) if it lands tails. Work by Furstenburg and Kesten guarantees that this sequence almost surely
Almost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
grows exponentially at a constant rate: the constant is independent of the coin tosses and was computed in 1999 by Divakar Viswanath. It is now known as Viswanath's constant
Viswanath's constant
In mathematics, the random Fibonacci sequence is a stochastic analogue of the Fibonacci sequence defined by the recurrence relation fn = fn−1 ± fn−2, where the signs + or − are chosen at random with equal probability 1/2, independently for different n...
.
A repfigit, or Keith number, is an integer such that, when its digits start a Fibonacci sequence with that number of digits, the original number is eventually reached. An example is 47, because the Fibonacci sequence starting with 4 and 7 (4,7,11,18,29,47) reaches 47. A repfigit can be a tribonacci sequence if there are 3 digits in the number, a tetranacci number if the number has four digits, etc. The first few repfigits are:
- 14, 19, 28, 47, 61, 75, 197, 742, 1104, 1537, 2208, 2580, 3684, 4788, 7385, 7647, 7909, …
Since the set of sequences satisfying the relation S(n) = S(n−1) + S(n−2) is closed under termwise addition and under termwise multiplication by a constant, it can be viewed as a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
. Any such sequence is uniquely determined by a choice of two elements, so the vector space is two-dimensional. If we abbreviate such a sequence as (S(0), S(1)), the Fibonacci sequence F(n) = (0, 1) and the shifted Fibonacci sequence F(n−1) = (1, 0) are seen to form a canonical basis for this space, yielding the identity:
- S(n) = S(0)F(n−1) + S(1)F(n)
for all such sequences S. For example, if S is the Lucas sequence 2, 1, 3, 4, 7, 11…, then we obtain
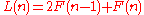 .
.