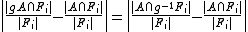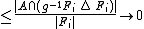Følner sequence
Encyclopedia
In mathematics
, a Følner sequence for a group
is a sequence
of sets satisfying a particular condition. If a group has a Følner sequence with respect to its action on itself, the group is amenable
. A more general notion of Følner nets
can be defined analogously, and is suited for the study of uncountable groups. Følner sequences are named for Erling Følner.
that acts
on a set
, a Følner sequence for the action is a sequence of finite subset
s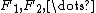
of 
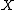which exhaust 
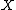and which "don't move too much" when acted on by any group element. Precisely,
Explanation of the notation used above:
Thus, what this definition says is that for any group element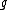
, the proportion of elements of 
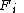that are moved away by 
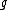goes to 0 as 
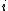gets large.
In the setting of a locally compact group
acting on a measure space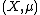
there is a more general definition. Instead of being finite, the sets are required to have finite, non-zero measure, and so the Følner requirement will be that
analogously to the discrete case. The standard case is that of the group acting on itself by left translation, in which case the measure in question is normally assumed to be the Haar measure.
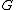and a Følner sequence 
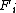, and we need to define a measure 
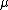on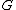 
, which philosophically speaking says how much of 
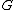any subset 
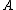takes up. The natural definition that uses our Følner sequence would be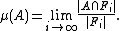
Of course, this limit doesn't necessarily exist. To overcome this technicality, we take an ultrafilter
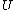on the natural numbers that contains intervals 
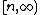. Then we use an ultralimit
instead of the regular limit
:
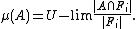
It turns out ultralimits have all the properties we need. Namely,
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Følner sequence for a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
is a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of sets satisfying a particular condition. If a group has a Følner sequence with respect to its action on itself, the group is amenable
Amenable group
In mathematics, an amenable group is a locally compact topological group G carrying a kind of averaging operation on bounded functions that is invariant under translation by group elements...
. A more general notion of Følner nets
Net (mathematics)
In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
can be defined analogously, and is suited for the study of uncountable groups. Følner sequences are named for Erling Følner.
Definition
Given a group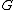 that actsGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on a set
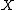, a Følner sequence for the action is a sequence of finite subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s
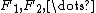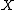of which exhaust 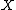and which "don't move too much" when acted on by any group element. Precisely,
- For every
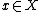, there exists some 
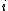such that 
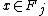for all 
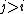, and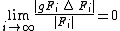
for all group elements 
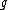in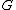 
.
Explanation of the notation used above:
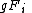is the result of the set 
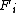being acted on the left by 
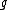. It consists of elements of the form 
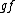for all 
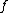in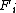 
.
is the symmetric differenceSymmetric differenceIn mathematics, the symmetric difference of two sets is the set of elements which are in either of the sets and not in their intersection. The symmetric difference of the sets A and B is commonly denoted by A\,\Delta\,B\,orA \ominus B....
operator.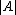
is the cardinality of a set 
.
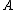Thus, what this definition says is that for any group element
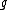, the proportion of elements of 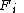that are moved away by 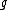goes to 0 as 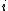gets large.In the setting of a locally compact group
Locally compact group
In mathematics, a locally compact group is a topological group G which is locally compact as a topological space. Locally compact groups are important because they have a natural measure called the Haar measure. This allows one to define integrals of functions on G.Many of the results of finite...
acting on a measure space
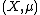there is a more general definition. Instead of being finite, the sets are required to have finite, non-zero measure, and so the Følner requirement will be that
-
,
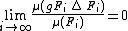analogously to the discrete case. The standard case is that of the group acting on itself by left translation, in which case the measure in question is normally assumed to be the Haar measure.
Examples
- Any finite group
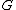trivially has a Følner sequence 
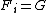for each 
.
- Consider the group of integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, acting on itself by addition. Let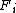
consist of the integers between 
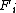and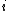 
. Then 
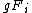consists of integers between 
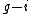and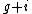 
. For large 
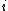, the symmetric difference has size 
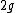, while 
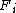has size 
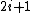. The resulting ratio is 
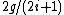, which goes to 0 as 
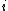gets large.
- With the original definition of Følner sequence, a countable group has a Følner sequence if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is amenable. An amenable groupAmenable groupIn mathematics, an amenable group is a locally compact topological group G carrying a kind of averaging operation on bounded functions that is invariant under translation by group elements...
has a Følner sequence if and only if it is countable. A group which has a Følner sequence is countable if and only if it is amenable.
- A locally compact group has a Følner sequence (with the generalized definition) if and only if it is amenable and second countable.
Proof of amenability
We have a group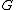 and a Følner sequence 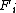, and we need to define a measure 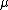on 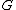, which philosophically speaking says how much of 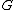any subset 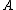takes up. The natural definition that uses our Følner sequence would be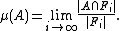Of course, this limit doesn't necessarily exist. To overcome this technicality, we take an ultrafilter
Ultrafilter
In the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
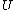on the natural numbers that contains intervals 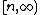. Then we use an ultralimitUltralimit
In mathematics, an ultralimit is a geometric construction that assigns to a sequence of metric spaces Xn a limiting metric space. The notion of an ultralimit captures the limiting behavior of finite configurations in the spaces Xn and uses an ultrafilter to avoid the process of repeatedly passing...
instead of the regular limit
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
:
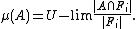
It turns out ultralimits have all the properties we need. Namely,
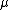is a probability measure. That is, 
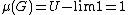, since the ultralimit coincides with the regular limit when it exists.
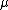is finitely additive. This is since ultralimits commute with addition just as regular limits do.
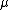is left invariant. This is since
- by the Følner sequence definition.