
Frobenius-Schur indicator
Encyclopedia
In mathematics
the Schur indicator, named after Issai Schur
, or Frobenius–Schur indicator describes what invariant bilinear forms a given irreducible representation of a compact group on a complex vector space has. It can be used to classify the irreducible representations of compact groups on real vector spaces.
of a compact group
G has character
χ its Frobenius-Schur indicator is defined to be

for Haar measure
μ with μ(G) = 1. When G is finite it is given by

The Frobenius-Schur indicator is always 1, 0, or -1. It provides a criterion for deciding whether an irreducible representation of G is real, complex or quaternionic, in a specific sense defined below. Below we discuss the case of finite group
s, but the general compact case is completely analogous.
Moreover every irreducible representation on a complex vector space can be constructed from a unique irreducible representation on a real vector space in one of the three ways above. So knowing the irreducible representations on complex spaces and their Schur indicators allows one to read off the irreducible representations on real spaces.
Real representations can be complexified to get a complex representation of the same dimension and complex representations can be converted into a real representation of twice the dimension by treating the real and imaginary components separately. Also, since all finite dimensional complex representations can be turned into a unitary representation for unitary representations, the dual representation is also a (complex) conjugate representation because the Hilbert space norm gives an antilinear bijective map from the representation to its dual representation.
Self-dual complex irreducible representation correspond to either real irreducible representation of the same dimension or real irreducible representations of twice the dimension called quaternionic representations (but not both) and non-self-dual complex irreducible representation correspond to a real irreducible representation of twice the dimension. Note for the latter case, both the complex irreducible representation and its dual give rise to the same real irreducible representation. An example of a quaternionic representation would be the four dimensional real irreducible representation of the quaternion group
Q8.

can be decomposed as the direct sum of two subrepresentations, the symmetric tensor product
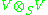
and the antisymmetric tensor product
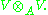
It's easy to show that
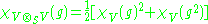
and
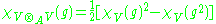
using a basis set.

and

are the number of copies of the trivial representation in
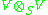
and

respectively. As observed above, if V is an irreducible representation,
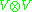
contains exactly one copy of the trivial representation if V is equivalent to its dual representation and no copies otherwise. For the former case, the trivial representation could either lie in the symmetric product, or the antisymmetric product.
The Frobenius-Schur indicator of an irreducible representation is always 1, 0, or −1. More precisely:

is a self-intertwiner, for any integer n,

is also a self-intertwiner. By Schur's lemma, this will be a multiple of the identity for irreducible representations. The trace of this self-intertwiner is called the nth Frobenius-Schur indicator.
The original case of the Frobenius-Schur indicator is that for n = 2. The zeroth indicator is the dimension of the irreducible representation, the first indicator would be 1 for the trivial representation and zero for the other irreducible representations.
It resembles the Casimir invariant
s for Lie algebra
irreducible representations. In fact, since any rep of G can be thought of as a module
for C[G] and vice versa, we can look at the center
of C[G]. This is analogous to looking at the center of the universal enveloping algebra
of a Lie algebra. It is simple to check that
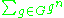
belongs to the center of C[G], which is simply the subspace of class functions on G.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
the Schur indicator, named after Issai Schur
Issai Schur
Issai Schur was a mathematician who worked in Germany for most of his life. He studied at Berlin...
, or Frobenius–Schur indicator describes what invariant bilinear forms a given irreducible representation of a compact group on a complex vector space has. It can be used to classify the irreducible representations of compact groups on real vector spaces.
Definition
If a finite-dimensional continuous complex representationRepresentation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
of a compact group
Compact group
In mathematics, a compact group is a topological group whose topology is compact. Compact groups are a natural generalisation of finite groups with the discrete topology and have properties that carry over in significant fashion...
G has character
Character theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
χ its Frobenius-Schur indicator is defined to be

for Haar measure
Haar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
μ with μ(G) = 1. When G is finite it is given by

The Frobenius-Schur indicator is always 1, 0, or -1. It provides a criterion for deciding whether an irreducible representation of G is real, complex or quaternionic, in a specific sense defined below. Below we discuss the case of finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s, but the general compact case is completely analogous.
Real irreducible representations
There are 3 types of irreducible real representations of a finite group on a real vector space V, as the ring of endomorphisms commuting with the group action can be isomorphic to either the real numbers, or the complex numbers, or the quaternions.- If the ring is the real numbers, then V⊗C is an irreducible complex representation with Schur indicator 1, also called a real representationReal representationIn the mathematical field of representation theory a real representation is usually a representation on a real vector space U, but it can also mean a representation on a complex vector space V with an invariant real structure, i.e., an antilinear equivariant mapj\colon V\to V\,which...
. - If the ring is the complex numbers, then V has two different conjugate complex structures, giving two irreducible complex representations with Schur indicator 0, sometimes called complex representationComplex representationThe term complex representation has slightly different meanings in mathematics and physics.In mathematics, a complex representation is a group representationof a group on a complex vector space....
s. - If the ring is the quaternion numbers, then choosing a subring of the quaternions isomorphic to the complex numbers makes V into an irreducible complex representation of G with Schur indicator −1, called a quaternionic representation.
Moreover every irreducible representation on a complex vector space can be constructed from a unique irreducible representation on a real vector space in one of the three ways above. So knowing the irreducible representations on complex spaces and their Schur indicators allows one to read off the irreducible representations on real spaces.
Real representations can be complexified to get a complex representation of the same dimension and complex representations can be converted into a real representation of twice the dimension by treating the real and imaginary components separately. Also, since all finite dimensional complex representations can be turned into a unitary representation for unitary representations, the dual representation is also a (complex) conjugate representation because the Hilbert space norm gives an antilinear bijective map from the representation to its dual representation.
Self-dual complex irreducible representation correspond to either real irreducible representation of the same dimension or real irreducible representations of twice the dimension called quaternionic representations (but not both) and non-self-dual complex irreducible representation correspond to a real irreducible representation of twice the dimension. Note for the latter case, both the complex irreducible representation and its dual give rise to the same real irreducible representation. An example of a quaternionic representation would be the four dimensional real irreducible representation of the quaternion group
Quaternion group
In group theory, the quaternion group is a non-abelian group of order eight, isomorphic to a certain eight-element subset of the quaternions under multiplication...
Q8.
Invariant bilinear forms
If V is the underlying vector space of a representation, then
can be decomposed as the direct sum of two subrepresentations, the symmetric tensor product
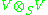
and the antisymmetric tensor product
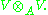
It's easy to show that
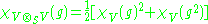
and
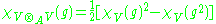
using a basis set.

and

are the number of copies of the trivial representation in
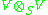
and

respectively. As observed above, if V is an irreducible representation,
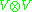
contains exactly one copy of the trivial representation if V is equivalent to its dual representation and no copies otherwise. For the former case, the trivial representation could either lie in the symmetric product, or the antisymmetric product.
The Frobenius-Schur indicator of an irreducible representation is always 1, 0, or −1. More precisely:
- It is 0 exactly when the irreducible representation has no invariant bilinear form, which is equivalent to saying that its character is not always real.
- It is 1 exactly when the irreducible representation has a symmetric invariant bilinear form. These are the representations that can be defined over the reals.
- It is −1 exactly when the irreducible representation has a skew symmetric invariant bilinear form. These are the representations whose character is real but that cannot be defined over the reals. They are less common than the other two cases.
Higher Frobenius-Schur indicators
Just as for any complex representation ρ,
is a self-intertwiner, for any integer n,

is also a self-intertwiner. By Schur's lemma, this will be a multiple of the identity for irreducible representations. The trace of this self-intertwiner is called the nth Frobenius-Schur indicator.
The original case of the Frobenius-Schur indicator is that for n = 2. The zeroth indicator is the dimension of the irreducible representation, the first indicator would be 1 for the trivial representation and zero for the other irreducible representations.
It resembles the Casimir invariant
Casimir invariant
In mathematics, a Casimir invariant or Casimir operator is a distinguished element of the centre of the universal enveloping algebra of a Lie algebra...
s for Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
irreducible representations. In fact, since any rep of G can be thought of as a module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
for C[G] and vice versa, we can look at the center
Center (algebra)
The term center or centre is used in various contexts in abstract algebra to denote the set of all those elements that commute with all other elements. It is often denoted Z, from German Zentrum, meaning "center". More specifically:...
of C[G]. This is analogous to looking at the center of the universal enveloping algebra
Universal enveloping algebra
In mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
of a Lie algebra. It is simple to check that
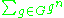
belongs to the center of C[G], which is simply the subspace of class functions on G.

