
First variation of area formula
Encyclopedia
In Riemannian geometry
, the first variation of area formula relates the mean curvature
of a hypersurface
to the rate of change of its area as it evolves in the outward normal direction.
Let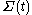 be a smooth family of oriented hypersurfaces in a Riemannian manifold
be a smooth family of oriented hypersurfaces in a Riemannian manifold
M such that the velocity of each point is given by the outward unit normal at that point. The first variation of area formula is
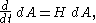
where dA is the area form on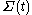 induced by the metric of M, and H is the mean curvature of
induced by the metric of M, and H is the mean curvature of 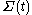 . The normal vector is parallel to
. The normal vector is parallel to 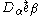 where
where 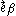 is the tangent vector. The mean curvature is parallel to the normal vector.
is the tangent vector. The mean curvature is parallel to the normal vector.
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, the first variation of area formula relates the mean curvature
Mean curvature
In mathematics, the mean curvature H of a surface S is an extrinsic measure of curvature that comes from differential geometry and that locally describes the curvature of an embedded surface in some ambient space such as Euclidean space....
of a hypersurface
Hypersurface
In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
to the rate of change of its area as it evolves in the outward normal direction.
Let
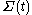 be a smooth family of oriented hypersurfaces in a Riemannian manifold
be a smooth family of oriented hypersurfaces in a Riemannian manifoldRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
M such that the velocity of each point is given by the outward unit normal at that point. The first variation of area formula is
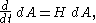
where dA is the area form on
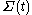 induced by the metric of M, and H is the mean curvature of
induced by the metric of M, and H is the mean curvature of 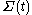 . The normal vector is parallel to
. The normal vector is parallel to 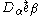 where
where 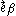 is the tangent vector. The mean curvature is parallel to the normal vector.
is the tangent vector. The mean curvature is parallel to the normal vector.

