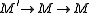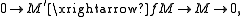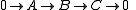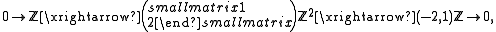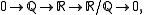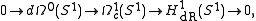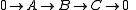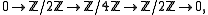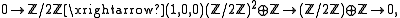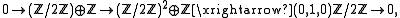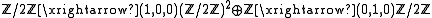Exact category
Encyclopedia
In mathematics
, an exact category is a concept of category theory
due to Daniel Quillen which is designed to encapsulate the properties of short exact sequences in abelian categories
without requiring that morphisms actually possess kernels and cokernels
, which is necessary for the usual definition of such a sequence.
possessing a class
E of "short exact sequences": triples of objects connected by arrows
satisfying the following axioms inspired by the properties of short exact sequences in an abelian category
:
Admissible monomorphisms are generally denoted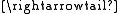 and admissible epimorphisms are denoted
and admissible epimorphisms are denoted 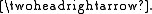 These axioms are not minimal; in fact, the last one has been shown by to be redundant.
These axioms are not minimal; in fact, the last one has been shown by to be redundant.
One can speak of an exact functor between exact categories exactly as in the case of exact functor
s of abelian categories: an exact functor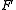 from an exact category D to another one E is an additive functor such that if
from an exact category D to another one E is an additive functor such that if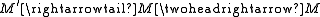
is exact in D, then
is exact in E. If D is a subcategory of E, it is an exact subcategory if the inclusion functor is fully faithful and exact.
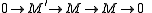
in A, then if are in E, so is
are in E, so is  . We can take the class E to be simply the sequences in E which are exact in A; that is,
. We can take the class E to be simply the sequences in E which are exact in A; that is,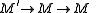
is in E iff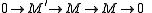
is exact in A. Then E is an exact category in the above sense. We verify the axioms:
Conversely, if E is any exact category, we can take A to be the category of left-exact functor
s from E into the category of abelian group
s, which is itself abelian and in which E is a natural subcategory (via the Yoneda embedding
, since Hom is left exact), stable under extensions, and in which a sequence is in E if and only if it is exact in A.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an exact category is a concept of category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
due to Daniel Quillen which is designed to encapsulate the properties of short exact sequences in abelian categories
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
without requiring that morphisms actually possess kernels and cokernels
Kernel (category theory)
In category theory and its applications to other branches of mathematics, kernels are a generalization of the kernels of group homomorphisms, the kernels of module homomorphisms and certain other kernels from algebra...
, which is necessary for the usual definition of such a sequence.
Definition
An exact category E is an additive categoryAdditive category
In mathematics, specifically in category theory, an additive category is a preadditive category C such that all finite collections of objects A1,...,An of C have a biproduct A1 ⊕ ⋯ ⊕ An in C....
possessing a class
Class (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
E of "short exact sequences": triples of objects connected by arrows
satisfying the following axioms inspired by the properties of short exact sequences in an abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
:
- E is closed under isomorphisms and contains the canonical ("split exact") sequences:
-
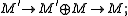
- Suppose
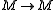 occurs as the second arrow of a sequence in E (it is an admissible epimorphism) and
occurs as the second arrow of a sequence in E (it is an admissible epimorphism) and 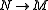 is any arrow in E. Then their pullbackPullback (category theory)In category theory, a branch of mathematics, a pullback is the limit of a diagram consisting of two morphisms f : X → Z and g : Y → Z with a common codomain; it is the limit of the cospan X \rightarrow Z \leftarrow Y...
is any arrow in E. Then their pullbackPullback (category theory)In category theory, a branch of mathematics, a pullback is the limit of a diagram consisting of two morphisms f : X → Z and g : Y → Z with a common codomain; it is the limit of the cospan X \rightarrow Z \leftarrow Y...
exists and its projection to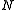 is also an admissible epimorphism. DuallyDual (category theory)In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
is also an admissible epimorphism. DuallyDual (category theory)In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
, if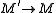 occurs as the first arrow of a sequence in E (it is an admissible monomorphism) and
occurs as the first arrow of a sequence in E (it is an admissible monomorphism) and 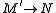 is any arrow, then their pushoutPushout (category theory)In category theory, a branch of mathematics, a pushout is the colimit of a diagram consisting of two morphisms f : Z → X and g : Z → Y with a common domain: it is the colimit of the span X \leftarrow Z \rightarrow Y.The pushout is the...
is any arrow, then their pushoutPushout (category theory)In category theory, a branch of mathematics, a pushout is the colimit of a diagram consisting of two morphisms f : Z → X and g : Z → Y with a common domain: it is the colimit of the span X \leftarrow Z \rightarrow Y.The pushout is the...
exists and its coprojection from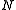 is also an admissible monomorphism. (We say that the admissible epimorphisms are "stable under pullback", resp. the admissible monomorphisms are "stable under pushout".);
is also an admissible monomorphism. (We say that the admissible epimorphisms are "stable under pullback", resp. the admissible monomorphisms are "stable under pushout".); - Admissible monomorphisms are kernelKernel (category theory)In category theory and its applications to other branches of mathematics, kernels are a generalization of the kernels of group homomorphisms, the kernels of module homomorphisms and certain other kernels from algebra...
s of their corresponding admissible epimorphisms and vice-versa. The composition of two admissible monomorphisms is admissible (likewise admissible epimorphisms); - Suppose
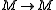 is a map in E which admits a kernel in E, and suppose
is a map in E which admits a kernel in E, and suppose 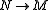 is any map such that the composition
is any map such that the composition  is an admissible epimorphism. Then so is
is an admissible epimorphism. Then so is 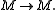 Dually, if
Dually, if 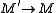 admits a cokernel and
admits a cokernel and 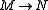 is such that
is such that 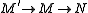 is an admissible monomorphism, then so is
is an admissible monomorphism, then so is 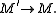
- Suppose
Admissible monomorphisms are generally denoted
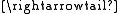 and admissible epimorphisms are denoted
and admissible epimorphisms are denoted 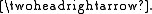 These axioms are not minimal; in fact, the last one has been shown by to be redundant.
These axioms are not minimal; in fact, the last one has been shown by to be redundant.One can speak of an exact functor between exact categories exactly as in the case of exact functor
Exact functor
In homological algebra, an exact functor is a functor, from some category to another, which preserves exact sequences. Exact functors are very convenient in algebraic calculations, roughly speaking because they can be applied to presentations of objects easily...
s of abelian categories: an exact functor
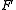 from an exact category D to another one E is an additive functor such that if
from an exact category D to another one E is an additive functor such that if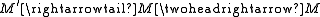
is exact in D, then

is exact in E. If D is a subcategory of E, it is an exact subcategory if the inclusion functor is fully faithful and exact.
Motivation
Exact categories come from abelian categories in the following way. Suppose A is abelian and let E be any strictly full additive subcategory which is closed under taking extensions in the sense that given an exact sequence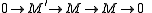
in A, then if
 are in E, so is
are in E, so is  . We can take the class E to be simply the sequences in E which are exact in A; that is,
. We can take the class E to be simply the sequences in E which are exact in A; that is,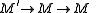
is in E iff
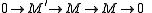
is exact in A. Then E is an exact category in the above sense. We verify the axioms:
- E is closed under isomorphisms and contains the split exact sequences: these are true by definition, since in an abelian category, any sequence isomorphic to an exact one is also exact, and since the split sequences are always exact in A.
- Admissible epimorphisms (respectively, admissible monomorphisms) are stable under pullbacks (resp. pushouts): given an exact sequence of objects in E,
-
- and a map
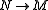 with
with 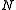 in E, one verifies that the following sequence is also exact; since E is stable under extensions, this means that
in E, one verifies that the following sequence is also exact; since E is stable under extensions, this means that 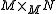 is in E:
is in E:
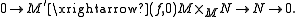
- Every admissible monomorphism is the kernel of its corresponding admissible epimorphism, and vice-versa: this is true as morphisms in A, and E is a full subcategory.
- If
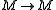 admits a kernel in E and if
admits a kernel in E and if 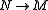 is such that
is such that 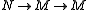 is an admissible epimorphism, then so is
is an admissible epimorphism, then so is  : See .
: See .
Conversely, if E is any exact category, we can take A to be the category of left-exact functor
Exact functor
In homological algebra, an exact functor is a functor, from some category to another, which preserves exact sequences. Exact functors are very convenient in algebraic calculations, roughly speaking because they can be applied to presentations of objects easily...
s from E into the category of abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s, which is itself abelian and in which E is a natural subcategory (via the Yoneda embedding
Yoneda lemma
In mathematics, specifically in category theory, the Yoneda lemma is an abstract result on functors of the type morphisms into a fixed object. It is a vast generalisation of Cayley's theorem from group theory...
, since Hom is left exact), stable under extensions, and in which a sequence is in E if and only if it is exact in A.
Examples
- Any abelian category is exact in the obvious way, according to the construction of #Motivation.
- A less trivial example is the category Abtf of torsion-free abelian groups, which is a strictly full subcategory of the (abelian) category Ab of all abelian groups. It is closed under extensions: if
-
- is a short exact sequence of abelian groups in which
 are torsion-free, then
are torsion-free, then 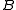 is seen to be torsion-free by the following argument: if
is seen to be torsion-free by the following argument: if 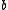 is a torsion element, then its image in
is a torsion element, then its image in 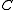 is zero, since
is zero, since 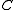 is torsion-free. Thus
is torsion-free. Thus 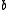 lies in the kernel of the map to
lies in the kernel of the map to 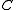 , which is
, which is 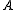 , but that is also torsion-free, so
, but that is also torsion-free, so  . By the construction of #Motivation, Abtf is an exact category; some examples of exact sequences in it are:
. By the construction of #Motivation, Abtf is an exact category; some examples of exact sequences in it are:
- where the last example is inspired by de Rham cohomologyDe Rham cohomologyIn mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
(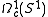 and
and 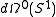 are the closed and exact differential formsClosed and exact differential formsIn mathematics, especially vector calculus and differential topology, a closed form is a differential form α whose exterior derivative is zero , and an exact form is a differential form that is the exterior derivative of another differential form β...
are the closed and exact differential formsClosed and exact differential formsIn mathematics, especially vector calculus and differential topology, a closed form is a differential form α whose exterior derivative is zero , and an exact form is a differential form that is the exterior derivative of another differential form β...
on the circle group); in particular, it is known that the cohomology group is isomorphic to the real numbers. This category is not abelian.- The following example is in some sense complementary to the above. Let Abt be the category of abelian groups with torsion (and also the zero group). This is additive and a strictly full subcategory of Ab again. It is even easier to see that it is stable under extensions: if
- is an exact sequence in which
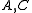 have torsion, then
have torsion, then 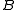 naturally has all the torsion elements of
naturally has all the torsion elements of 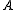 . Thus it is an exact category; some examples of its exact sequences are
. Thus it is an exact category; some examples of its exact sequences are
- where in the second example, the
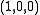 means inclusion as the first summand, and in the last example, the
means inclusion as the first summand, and in the last example, the 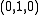 means projection onto the second summand. One interesting feature of this category is that it illustrates that the notion of cohomology does not make sense in general exact categories: for consider the "complex"
means projection onto the second summand. One interesting feature of this category is that it illustrates that the notion of cohomology does not make sense in general exact categories: for consider the "complex"
- which is obtained by pasting the marked arrows in the last two examples above. The second arrow is an admissible epimorphism, and its kernel is (from the last example),
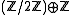 . Since the two arrows compose to zero, the first arrow factors through this kernel, and in fact the factorization is the inclusion as the first summand. Thus the quotient, if it were to exist, would have to be
. Since the two arrows compose to zero, the first arrow factors through this kernel, and in fact the factorization is the inclusion as the first summand. Thus the quotient, if it were to exist, would have to be 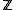 , which is not actually in Abt. That is, the cohomology of this complex is undefined.
, which is not actually in Abt. That is, the cohomology of this complex is undefined.