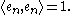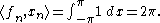In functional analysis

Functional analysis

Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...

, the Dunford–Pettis property, named after Nelson Dunford

Nelson Dunford

Nelson Dunford was an American mathematician, known for his work in functional analysis, namely integration of vector valued functions, ergodic theory, and linear operators. The Dunford decomposition, Dunford–Pettis property, and Dunford-Schwartz theorem bear his name.He studied mathematics at the...

 and B. J. Pettis, is a property of a Banach space

Banach space

In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...

 stating that all weakly compact operators from this space into another Banach space are completely continuous. Many standard Banach spaces have this property, most notably, the space C(K) of continuous functions on a compact space

Compact space

In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...

 and the space L¹(μ)

Lp space

In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...

 of the Lebesgue integrable functions on a measure space. Alexander Grothendieck

Alexander Grothendieck

Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...

 introduced the concept in the early 1950s , following the work of Dunford and Pettis, who developed earlier results of Shizuo Kakutani

Shizuo Kakutani

was a Japanese-born American mathematician, best known for his eponymous fixed-point theorem.Kakutani attended Tohoku University in Sendai, where his advisor was Tatsujirō Shimizu. Early in his career he spent two years at the Institute for Advanced Study in Princeton at the invitation of the...

, Kōsaku Yosida

Kosaku Yosida

was a Japanese mathematician who worked in the field of functional analysis. He is known for the Hille-Yosida theorem concerning C0-semigroups.- References :...

, and several others. Important results were obtained more recently by Jean Bourgain

Jean Bourgain

Jean Bourgain is a Belgian mathematician. He has been a faculty member at the University of Illinois, Urbana-Champaign and, from 1985 until 1995, professor at Institut des Hautes Études Scientifiques at Bures-sur-Yvette in France, and since 1994 at the Institute for Advanced Study in Princeton,...

. Nevertheless, the Dunford–Pettis property is not completely understood.

Definition

A Banach space X has the Dunford–Pettis property if every continuous weakly compact operator

Compact operator

In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...

 T: X → Y from X into another Banach space Y transforms weakly compact sets in X into norm-compact sets in Y (such operators are called completely continuous). An important equivalent definition is that for any weakly convergent

Weak topology

In mathematics, weak topology is an alternative term for initial topology. The term is most commonly used for the initial topology of a topological vector space with respect to its continuous dual...

 sequences (x_n) of X and (f_n) of the dual space

Dual space

In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...

 X^∗, converging (weakly) to x and f, the sequence f_n(x_n) converges to f(x).

Counterexamples

• The second definition may appear counterintuitive at first, but consider an orthonormal basis e_n of a separable Hilbert space H. Then e_n → 0 weakly, but for all n,

Thus separable Hilbert spaces cannot have the Dunford–Pettis property.

• Consider as another example the space L^p(−π,π) where 1<p<∞. The sequences x_n=e^inx in L^p and f_n=e^inx in L^q = (L^p)* both converge weakly to zero. But

• More generally, no infinite-dimensional reflexive Banach space may have the Dunford–Pettis property. In particular, a Hilbert space
  Hilbert space
  The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
  
   and more generally, Lp space
  Lp space
  In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
  
  s with 1 < p < ∞ do not possess this property.

Examples

• If X is a compact Hausdorff space, then the Banach space C(X) of continuous function
  Continuous function
  In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
  
  s with the uniform norm has the Dunford-Pettis property.