Drinker paradox
Encyclopedia
The drinker paradox is a theorem
of classical
predicate logic
that states: There is someone in the pub such that, if he is drinking, everyone in the pub is drinking. The actual theorem is
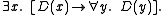
The paradox
was popularised by the mathematical logician Raymond Smullyan
, who called it the "drinking principle" in his book What Is the Name of this Book?
) is false.
The proof begins by recognizing it is true that either everyone in the pub is drinking (in this particular round of drinks), or at least one person in the pub isn't drinking.
On the one hand, suppose everyone is drinking. For any particular person, it can't be wrong to say that if that particular person is drinking, then everyone in the pub is drinking — because everyone is drinking.
Because everyone is drinking, then that one person must drink because when ' that person ' drinks ' everybody ' drinks, everybody includes that person.
Suppose, on the other hand, that at least one person isn't drinking. For any particular nondrinking person, it still can't be wrong to say that if that particular person is drinking, then everyone in the pub is drinking — because that person is, in fact, not drinking. In this case the condition is false, so the statement is true.
Either way, there is someone in the pub such that, if he is drinking, everyone in the pub is drinking. Hence the paradox.
is built into the inference rules of classical predicate logic. We can deduce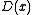
from 
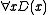, but of course if the domain were empty (in this case, if there were nobody in the pub), the proposition 
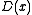is not well-formed for any closed expression 
.
Nevertheless, free logic
, which allows for empty domains, still has something like the drinker paradox in the form of the theorem:
Or in words:
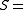"everyone is drinking", which is always available in classical logic. If the logic does not admit arbitrary excluded middle—for example if the logic is intuitionistic
—then the truth of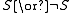
must first be established, i.e., 
must be shown to be decidable
.
As a simple example of one such decision procedure, if there are finitely many customers in the pub, one can find one person who doesn't drink. But if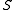
is given no semantics
, then there is no proof of the drinker paradox in intuitionistic logic
. Indeed, assuming the drinkinginfinite domains leads to various classically valid but intuitionistically unacceptable conclusions.
For instance, it would allow for a simple solution of Goldbach's conjecture
, which is one of the oldest unsolved problems in mathematics. It asks whether all even numbers greater than two can be expressed as the sum of two prime number
s. Applying the drinking principle, it would follow that there exists an even number greater than two, such that, if it is the sum of two primes suffice to check whether that particular number is the sum of two primes, which has a finite decision process. If it were not, then obviously it would be a refutation of the conjecture. But if it were, then all of them would be, and the conjecture would be proven.
Nevertheless, intuitionistic (free) logic still has something like the drinker paradox in the form of the theorem: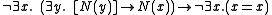
If we tak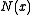e
to be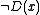 
, that is, x is not drinking, then in words this reads:
In classical logic this would be equivalent to the previous statement, from which it can be derived by two transpositions
.
. It has the property that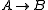
is true if B is true or if A is false (in classical logic, but not intuitionistic logic, this is also a necessary condition).
So as it was applied here, the statement "if he is drinking, everyone is drinking" was taken to be correct in one case, if everyone was drinking, and in the other case, if he was not drinking — even though his drinking may not have had anything to do with anyone else's drinking.
In natural language, on the other hand, typically "if...then..." is used as an indicative conditional
.
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
of classical
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
predicate logic
Predicate logic
In mathematical logic, predicate logic is the generic term for symbolic formal systems like first-order logic, second-order logic, many-sorted logic or infinitary logic. This formal system is distinguished from other systems in that its formulae contain variables which can be quantified...
that states: There is someone in the pub such that, if he is drinking, everyone in the pub is drinking. The actual theorem is
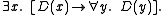
The paradox
Paradox
Similar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...
was popularised by the mathematical logician Raymond Smullyan
Raymond Smullyan
Raymond Merrill Smullyan is an American mathematician, concert pianist, logician, Taoist philosopher, and magician.Born in Far Rockaway, New York, his first career was stage magic. He then earned a BSc from the University of Chicago in 1955 and his Ph.D. from Princeton University in 1959...
, who called it the "drinking principle" in his book What Is the Name of this Book?
Proof of the paradox
The paradox is valid due to the nature of material implication in formal logic, which states that "If P, then Q" is always true if P (the condition or antecedentAntecedent (logic)
An antecedent is the first half of a hypothetical proposition.Examples:* If P, then Q.This is a nonlogical formulation of a hypothetical proposition...
) is false.
The proof begins by recognizing it is true that either everyone in the pub is drinking (in this particular round of drinks), or at least one person in the pub isn't drinking.
On the one hand, suppose everyone is drinking. For any particular person, it can't be wrong to say that if that particular person is drinking, then everyone in the pub is drinking — because everyone is drinking.
Because everyone is drinking, then that one person must drink because when ' that person ' drinks ' everybody ' drinks, everybody includes that person.
Suppose, on the other hand, that at least one person isn't drinking. For any particular nondrinking person, it still can't be wrong to say that if that particular person is drinking, then everyone in the pub is drinking — because that person is, in fact, not drinking. In this case the condition is false, so the statement is true.
Either way, there is someone in the pub such that, if he is drinking, everyone in the pub is drinking. Hence the paradox.
Discussion
This proof illustrates several properties of classical predicate logic that do not always agree with ordinary language.Non-empty domain
First, we didn't need to assume there was anyone in the pub. The assumption that the domain is non-emptyEmpty domain
In first-order logic the empty domain is the empty set having no members. In traditional and classical logic domains are restrictedly non-empty in order that certain theorems be valid. Interpretations with an empty domain are shown to be a trivial case by a convention originating at least in 1927...
is built into the inference rules of classical predicate logic. We can deduce
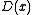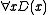from , but of course if the domain were empty (in this case, if there were nobody in the pub), the proposition 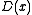is not well-formed for any closed expression .Nevertheless, free logic
Free logic
A free logic is a logic with fewer existential presuppositions than classical logic. Free logics may allow for terms that do not denote any object. Free logics may also allow models that have an empty domain...
, which allows for empty domains, still has something like the drinker paradox in the form of the theorem:
Or in words:
- If there is anyone in the pub at all, then there is someone such that, if they are drinking, then everyone in the pub is drinking.
Excluded middle
The above proof begins by saying that either everyone is drinking, or someone is not drinking. This uses the validity of excluded middle for the statement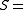 "everyone is drinking", which is always available in classical logic. If the logic does not admit arbitrary excluded middle—for example if the logic is intuitionisticIntuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
—then the truth of
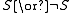must first be established, i.e., must be shown to be decidableDecidability (logic)
In logic, the term decidable refers to the decision problem, the question of the existence of an effective method for determining membership in a set of formulas. Logical systems such as propositional logic are decidable if membership in their set of logically valid formulas can be effectively...
.
As a simple example of one such decision procedure, if there are finitely many customers in the pub, one can find one person who doesn't drink. But if
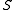is given no semanticsSemantics
Semantics is the study of meaning. It focuses on the relation between signifiers, such as words, phrases, signs and symbols, and what they stand for, their denotata....
, then there is no proof of the drinker paradox in intuitionistic logic
Intuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
. Indeed, assuming the drinkinginfinite domains leads to various classically valid but intuitionistically unacceptable conclusions.
For instance, it would allow for a simple solution of Goldbach's conjecture
Goldbach's conjecture
Goldbach's conjecture is one of the oldest unsolved problems in number theory and in all of mathematics. It states:A Goldbach number is a number that can be expressed as the sum of two odd primes...
, which is one of the oldest unsolved problems in mathematics. It asks whether all even numbers greater than two can be expressed as the sum of two prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s. Applying the drinking principle, it would follow that there exists an even number greater than two, such that, if it is the sum of two primes suffice to check whether that particular number is the sum of two primes, which has a finite decision process. If it were not, then obviously it would be a refutation of the conjecture. But if it were, then all of them would be, and the conjecture would be proven.
Nevertheless, intuitionistic (free) logic still has something like the drinker paradox in the form of the theorem:
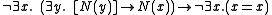
If we take
to be 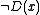, that is, x is not drinking, then in words this reads:
- If there isn't someone in the pub such that, if anyone in the pub isn't drinking, then they aren't drinking either, then nobody is in the pub.
In classical logic this would be equivalent to the previous statement, from which it can be derived by two transpositions
Transposition (logic)
In the methods of deductive reasoning in classical logic, transposition is the rule of inference that permits one to infer from the truth of "A implies B" the truth of "Not-B implies not-A", and conversely. Its symbolic expression is:...
.
Material versus indicative conditional
Most important to the paradox is that the conditional in classical (and intuitionistic) logic is the material conditionalMaterial conditional
The material conditional, also known as material implication, is a binary truth function, such that the compound sentence p→q is logically equivalent to the negative compound: not . A material conditional compound itself is often simply called a conditional...
. It has the property that
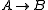is true if B is true or if A is false (in classical logic, but not intuitionistic logic, this is also a necessary condition).So as it was applied here, the statement "if he is drinking, everyone is drinking" was taken to be correct in one case, if everyone was drinking, and in the other case, if he was not drinking — even though his drinking may not have had anything to do with anyone else's drinking.
In natural language, on the other hand, typically "if...then..." is used as an indicative conditional
Indicative conditional
In natural languages, an indicative conditional is the logical operation given by statements of the form "If A then B". Unlike the material conditional, an indicative conditional does not have a stipulated definition...
.