
Dickson polynomial
Encyclopedia
In mathematics
, the Dickson polynomials, denoted Dn(x,α), form a polynomial sequence
studied by .
Over the complex numbers, Dickson polynomials are essentially equivalent to Chebyshev polynomials with a change of variable, and in fact Dickson polynomials are sometimes called Chebyshev polynomials.
Dickson polynomials are mainly studied over finite fields, when they are not equivalent to Chebyshev polynomials. One of the main reasons for interest in them is that for fixed α, they give many examples of permutation polynomials: polynomials acting as permutations of finite fields.

The first few Dickson polynomials are
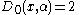
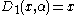


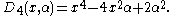
The Dickson polynomials of the second kind En are defined by

They have not been studied much, and have properties similar to those of Dickson polynomials of the first kind.
The first few Dickson polynomials of the second kind are
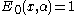
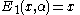
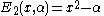

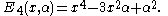
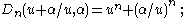
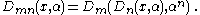
For n≥2 the Dickson polynomials satisfy the recurrence relation

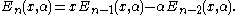
The Dickson polynomial Dn = y is a solution of the ordinary differential equation
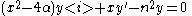
and the Dickson polynomial En = y is a solution of the differential equation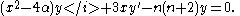
Their ordinary generating functions are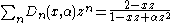
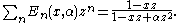
Crucially, the Dickson polynomial Dn(x,a) can be defined over rings in which a is not a square, and over rings of characteristic 2; in these cases, Dn(x,a) is often not related to a Chebyshev polynomial.
The Dickson polynomial Dn(x,α) (considered as a function of x with α fixed) is a permutation polynomial for the field with q elements whenever n is coprime to q2−1.
M. proved that any integral polynomial that is a permutation polynomial for infinitely many prime fields is a composition of Dickson polynomials and linear polynomials (with rational coefficients). This assertion has become known as Schur's conjecture, although in fact Schur did not make this conjecture. Since Fried's paper contained numerous errors, a corrected account was given by G. , and subsequently P. gave a simpler proof along the lines of an argument due to Schur.
Further, P. proved that any permutation polynomial over the finite field Fq whose degree is simultaneously coprime to q−1 and less than q1/4 must be a composition of Dickson polynomials and linear polynomials.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Dickson polynomials, denoted Dn(x,α), form a polynomial sequence
Polynomial sequence
In mathematics, a polynomial sequence is a sequence of polynomials indexed by the nonnegative integers 0, 1, 2, 3, ..., in which each index is equal to the degree of the corresponding polynomial...
studied by .
Over the complex numbers, Dickson polynomials are essentially equivalent to Chebyshev polynomials with a change of variable, and in fact Dickson polynomials are sometimes called Chebyshev polynomials.
Dickson polynomials are mainly studied over finite fields, when they are not equivalent to Chebyshev polynomials. One of the main reasons for interest in them is that for fixed α, they give many examples of permutation polynomials: polynomials acting as permutations of finite fields.
Definition
D0(x,α) = 2, and for n > 0 Dickson polynomials (of the first kind) are given by
The first few Dickson polynomials are
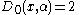
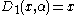


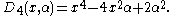
The Dickson polynomials of the second kind En are defined by

They have not been studied much, and have properties similar to those of Dickson polynomials of the first kind.
The first few Dickson polynomials of the second kind are
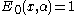
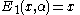
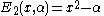

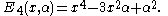
Properties
The Dn satisfy the identities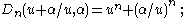
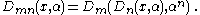
For n≥2 the Dickson polynomials satisfy the recurrence relation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....

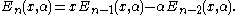
The Dickson polynomial Dn = y is a solution of the ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
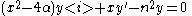
and the Dickson polynomial En = y is a solution of the differential equation
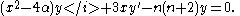
Their ordinary generating functions are
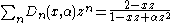
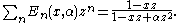
Links to other polynomials
- Dickson polynomials over the complex numbers are related to Chebyshev polynomials Tn and Un by
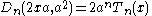
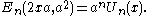
Crucially, the Dickson polynomial Dn(x,a) can be defined over rings in which a is not a square, and over rings of characteristic 2; in these cases, Dn(x,a) is often not related to a Chebyshev polynomial.
- The Dickson polynomials with parameter α = 1 or α = -1 are related to the Fibonacci and Lucas polynomials.
- The Dickson polynomials with parameter α = 0 give monomials:
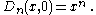
Permutation polynomials and Dickson polynomials
A permutation polynomial (for a given finite field) is one that acts as a permutation of the elements of the finite field.The Dickson polynomial Dn(x,α) (considered as a function of x with α fixed) is a permutation polynomial for the field with q elements whenever n is coprime to q2−1.
M. proved that any integral polynomial that is a permutation polynomial for infinitely many prime fields is a composition of Dickson polynomials and linear polynomials (with rational coefficients). This assertion has become known as Schur's conjecture, although in fact Schur did not make this conjecture. Since Fried's paper contained numerous errors, a corrected account was given by G. , and subsequently P. gave a simpler proof along the lines of an argument due to Schur.
Further, P. proved that any permutation polynomial over the finite field Fq whose degree is simultaneously coprime to q−1 and less than q1/4 must be a composition of Dickson polynomials and linear polynomials.

