Cyclotomic polynomial
Encyclopedia
In algebra
, the nth cyclotomic polynomial, for any positive integer
n, is the monic polynomial:
where the product is over all nth primitive roots of unity ω in a field, i.e. all the complex numbers ω of order
n.
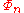, or in other words the number of factors in its definition above, is φ(n), where φ is Euler's totient function
.
The coefficients of
are integers, in other words, 
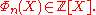This can be seen elementarily by expressing the coefficients of the polynomials as elementary symmetric polynomial
s of the primitive roots, and to proceed inductively by using the relation: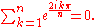
The fundamental relation involving cyclotomic polynomials is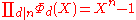
which amounts to the fact that each n-th root of unity is, for some divisor d of n, a primitive d-th root of unity.
The Möbius inversion formula yields the equivalent formulation:
where μ is the Möbius function
.
From this fact, or alternatively, directy from the fact that the roots of a cyclotomic polynomial are the primitive roots of unity, we can calculate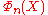
by dividing 
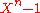by the cyclotomic polynomials of the proper divisors of n:
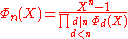
(Recall that
. )
The polynomial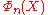
is irreducible
in the ring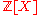
. This result, due to Gauss
, is not trivial. The case of prime
n is easier to prove than the general case, thanks to Eisenstein's criterion.
, say pm where p is prime, then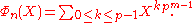
In particular ( for m = 1)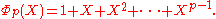
Any cyclotomic polynomial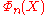
has a simple expression in terms of 
where q is the radical of n:
If
is odd, then 
.
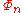are all in the set {1, −1, 0}.
The first cyclotomic polynomial with 3 different odd prime factors is
and it has a coefficient −2 (see its expression below). The converse isn't true: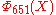 
= 
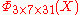only has coefficients in {1, −1, 0}.
If n is a product of more odd different prime factors, the coefficients may increase to very high values. E.g.,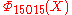
= 
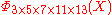has coefficients running from −22 to 22, 
= 
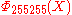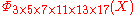, the smallest n with 6 different odd primes, has coefficients up to ±532.
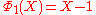
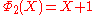
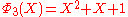
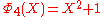
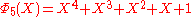
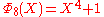
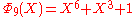
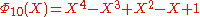
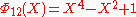
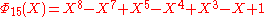
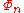is irreducible, one can prove the infinitude of prime
s congruent
to 1 modulo n, which is a special case of Dirichlet's theorem on arithmetic progressions
.
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, the nth cyclotomic polynomial, for any positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
n, is the monic polynomial:
where the product is over all nth primitive roots of unity ω in a field, i.e. all the complex numbers ω of order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
n.
Fundamental tools
The degree of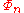, or in other words the number of factors in its definition above, is φ(n), where φ is Euler's totient functionEuler's totient function
In number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
.
The coefficients of
are integers, in other words, 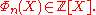This can be seen elementarily by expressing the coefficients of the polynomials as elementary symmetric polynomialElementary symmetric polynomial
In mathematics, specifically in commutative algebra, the elementary symmetric polynomials are one type of basic building block for symmetric polynomials, in the sense that any symmetric polynomial P can be expressed as a polynomial in elementary symmetric polynomials: P can be given by an...
s of the primitive roots, and to proceed inductively by using the relation:
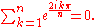
The fundamental relation involving cyclotomic polynomials is
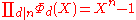
which amounts to the fact that each n-th root of unity is, for some divisor d of n, a primitive d-th root of unity.
The Möbius inversion formula yields the equivalent formulation:
where μ is the Möbius function
Möbius function
The classical Möbius function μ is an important multiplicative function in number theory and combinatorics. The German mathematician August Ferdinand Möbius introduced it in 1832...
.
From this fact, or alternatively, directy from the fact that the roots of a cyclotomic polynomial are the primitive roots of unity, we can calculate
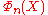by dividing 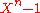by the cyclotomic polynomials of the proper divisors of n: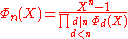(Recall that
. )The polynomial
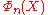is irreducibleIrreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
in the ring
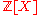. This result, due to GaussCarl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
, is not trivial. The case of prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
n is easier to prove than the general case, thanks to Eisenstein's criterion.
Cyclotomic polynomials and arithmetic of integers
If n is a prime powerPrime power
In mathematics, a prime power is a positive integer power of a prime number.For example: 5=51, 9=32 and 16=24 are prime powers, while6=2×3, 15=3×5 and 36=62=22×32 are not...
, say pm where p is prime, then
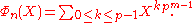
In particular ( for m = 1)
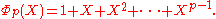
Any cyclotomic polynomial
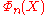has a simple expression in terms of where q is the radical of n:If
is odd, then .Integers appearing as coefficients
If n has at most two distinct odd prime factors, then Migotti showed that the coefficients of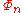 are all in the set {1, −1, 0}.The first cyclotomic polynomial with 3 different odd prime factors is
and it has a coefficient −2 (see its expression below). The converse isn't true: 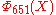= 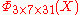only has coefficients in {1, −1, 0}.If n is a product of more odd different prime factors, the coefficients may increase to very high values. E.g.,
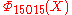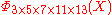= has coefficients running from −22 to 22, 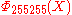= 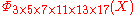, the smallest n with 6 different odd primes, has coefficients up to ±532.List of the first cyclotomic polynomials
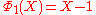
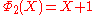
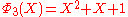
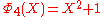
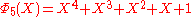
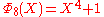
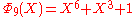
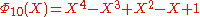
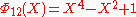
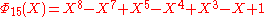
Applications
Using the fact that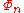 is irreducible, one can prove the infinitude of primePrime
A prime is a natural number that has exactly two distinct natural number divisors: 1 and itself.Prime or PRIME may also refer to:In mathematics:*Prime , the ′ mark, typically used as a suffix...
s congruent
Congruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
to 1 modulo n, which is a special case of Dirichlet's theorem on arithmetic progressions
Dirichlet's theorem on arithmetic progressions
In number theory, Dirichlet's theorem, also called the Dirichlet prime number theorem, states that for any two positive coprime integers a and d, there are infinitely many primes of the form a + nd, where n ≥ 0. In other words, there are infinitely many primes which are...
.