.gif)
Cycle graph (algebra)
Encyclopedia
In group theory
, a sub-field of abstract algebra
, a group cycle graph illustrates the various cycle
s of a group
and is particularly useful in visualizing the structure of small finite group
s. For groups with fewer than 16 elements, the cycle graph determines the group (up to
isomorphism
).
A cycle is the set of powers of a given group element a; where an, the n-th power of an element a, is defined as the product of a multiplied by itself n times. The element a is said to generate the cycle. In a finite group, some non-zero power of a must be the group identity
, e; the lowest such power is the order of the cycle, the number of distinct elements in it. In a cycle graph, the cycle is represented as a series of polygons, with the vertices representing the group elements, and
the connecting lines indicating that all elements in that polygon are members of the same cycle.
If a generates a cycle of order 6 (or, more shortly, has order 6), then a6 = e. Then the set of powers of a², {a², a4, e} is a cycle, but this is really no new information. Similarly, a5 generates the same cycle as a itself.
So, we only need to consider the primitive cycles, those that are not subsets of another cycle. Each of these is generated by some primitive element, a. Take one point
for each element of the original group. For each primitive element, connect e to a, a to a², ... an-1 to an, ... until you come back to e. The result is the cycle graph.
(Technically, the above description implies that if a² = e, so a has order 2 (is an involution), it's connected to e by two edges. It's conventional to only use one.)
Dih4. The multiplication table for this group is shown on the left, and the cycle graph is shown on the right with e specifying the identity element.
Notice the cycle e, a, a², a³ . It can be seen from the multiplication table that successive powers of a in fact behave this way. The reverse case is also true. In other words: (a³)²=a² , (a³)³=a and (a³)4=e . This behavior is true for any cycle in any group - a cycle may be traversed in either direction.
 Cycles that contain a non-prime number of elements implicitly have cycles that are not connected in the graph. For the group Dih4 above, we might want to draw a line between a² and e since (a²)²=e but since a² is part of a larger cycle, this is not done.
Cycles that contain a non-prime number of elements implicitly have cycles that are not connected in the graph. For the group Dih4 above, we might want to draw a line between a² and e since (a²)²=e but since a² is part of a larger cycle, this is not done.
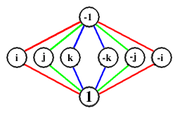
There can be ambiguity when two cycles share an element that is not the identity element. Consider for example, the simple quaternion group
, whose cycle graph is shown on the right. Each of the elements in the middle row when multiplied by itself gives -1 (where 1 is the identity element). In this case we may use different colors to keep track of the cycles, although symmetry considerations will work as well.
As above, the 2-element cycles should be connected by two lines, but this is usually abbreviated by a single line.
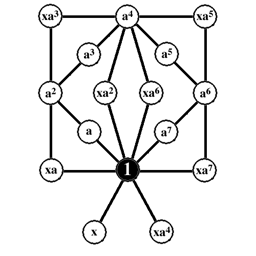
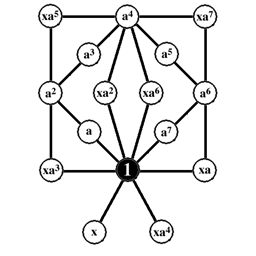
Two distinct groups may have cycle graphs that have the same structure, and can only be distinguished by the product table, or by labeling the elements in the graph in terms of
the groups basic elements. The lowest order for which this problem can occur is order 16 in the case of Z2 x Z8 and the modular group
, as shown below. (Note - the cycles with common elements are distinguished by symmetry in these graphs.)
The multiplication table of Z2 x Z8 is shown below:
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, a sub-field of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a group cycle graph illustrates the various cycle
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
s of a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
and is particularly useful in visualizing the structure of small finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s. For groups with fewer than 16 elements, the cycle graph determines the group (up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
).
A cycle is the set of powers of a given group element a; where an, the n-th power of an element a, is defined as the product of a multiplied by itself n times. The element a is said to generate the cycle. In a finite group, some non-zero power of a must be the group identity
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
, e; the lowest such power is the order of the cycle, the number of distinct elements in it. In a cycle graph, the cycle is represented as a series of polygons, with the vertices representing the group elements, and
the connecting lines indicating that all elements in that polygon are members of the same cycle.
Cycles
Cycles can overlap, or they can have no element in common but the identity. The cycle graph displays each interesting cycle as a polygon.If a generates a cycle of order 6 (or, more shortly, has order 6), then a6 = e. Then the set of powers of a², {a², a4, e} is a cycle, but this is really no new information. Similarly, a5 generates the same cycle as a itself.
So, we only need to consider the primitive cycles, those that are not subsets of another cycle. Each of these is generated by some primitive element, a. Take one point
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
for each element of the original group. For each primitive element, connect e to a, a to a², ... an-1 to an, ... until you come back to e. The result is the cycle graph.
(Technically, the above description implies that if a² = e, so a has order 2 (is an involution), it's connected to e by two edges. It's conventional to only use one.)
Properties
As an example of a group cycle graph, consider the dihedral groupDihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
Dih4. The multiplication table for this group is shown on the left, and the cycle graph is shown on the right with e specifying the identity element.
| o | e | b | a | a2 | a3 | ab | a2b | a3b |
|---|---|---|---|---|---|---|---|---|
| e | e | b | a | a2 | a3 | ab | a2b | a3b |
| b | b | e | a3b | a2b | ab | a3 | a2 | a |
| a | a | ab | a2 | a3 | e | a2b | a3b | b |
| a2 | a2 | a2b | a3 | e | a | a3b | b | ab |
| a3 | a3 | a3b | e | a | a2 | b | ab | a2b |
| ab | ab | a | b | a3b | a2b | e | a3 | a2 |
| a2b | a2b | a2 | ab | b | a3b | a | e | a3 |
| a3b | a3b | a3 | a2b | ab | b | a2 | a | e |
Notice the cycle e, a, a², a³ . It can be seen from the multiplication table that successive powers of a in fact behave this way. The reverse case is also true. In other words: (a³)²=a² , (a³)³=a and (a³)4=e . This behavior is true for any cycle in any group - a cycle may be traversed in either direction.

There can be ambiguity when two cycles share an element that is not the identity element. Consider for example, the simple quaternion group
Quaternion group
In group theory, the quaternion group is a non-abelian group of order eight, isomorphic to a certain eight-element subset of the quaternions under multiplication...
, whose cycle graph is shown on the right. Each of the elements in the middle row when multiplied by itself gives -1 (where 1 is the identity element). In this case we may use different colors to keep track of the cycles, although symmetry considerations will work as well.
As above, the 2-element cycles should be connected by two lines, but this is usually abbreviated by a single line.
Two distinct groups may have cycle graphs that have the same structure, and can only be distinguished by the product table, or by labeling the elements in the graph in terms of
the groups basic elements. The lowest order for which this problem can occur is order 16 in the case of Z2 x Z8 and the modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
, as shown below. (Note - the cycles with common elements are distinguished by symmetry in these graphs.)


The multiplication table of Z2 x Z8 is shown below:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 3 | 2 | 5 | 4 | 7 | 6 | 9 | 8 | 11 | 10 | 13 | 12 | 15 | 14 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 0 | 1 |
| 3 | 2 | 5 | 4 | 7 | 6 | 9 | 8 | 11 | 10 | 13 | 12 | 15 | 14 | 1 | 0 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 0 | 1 | 2 | 3 |
| 5 | 4 | 7 | 6 | 9 | 8 | 11 | 10 | 13 | 12 | 15 | 14 | 1 | 0 | 3 | 2 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 0 | 1 | 2 | 3 | 4 | 5 |
| 7 | 6 | 9 | 8 | 11 | 10 | 13 | 12 | 15 | 14 | 1 | 0 | 3 | 2 | 5 | 4 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 9 | 8 | 11 | 10 | 13 | 12 | 15 | 14 | 1 | 0 | 3 | 2 | 5 | 4 | 7 | 6 |
| 10 | 11 | 12 | 13 | 14 | 15 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 11 | 10 | 13 | 12 | 15 | 14 | 1 | 0 | 3 | 2 | 5 | 4 | 7 | 6 | 9 | 8 |
| 12 | 13 | 14 | 15 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 13 | 12 | 15 | 14 | 1 | 0 | 3 | 2 | 5 | 4 | 7 | 6 | 9 | 8 | 11 | 10 |
| 14 | 15 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 15 | 14 | 1 | 0 | 3 | 2 | 5 | 4 | 7 | 6 | 9 | 8 | 11 | 10 | 13 | 12 |
Other information derivable from cycle graphs
- The inverse of an element could be identified in the cycle graph. It is the element whose distance is the same from the opposite direction.
Graph characteristics of particular group families
Certain group types give typical graphs:- Cyclic groupCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
s Zn is a single cycle graphed simply as an n-sided polygon with the elements at the vertices.
 |  |  |  | 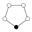 | 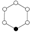 |  |  |
|---|---|---|---|---|---|---|---|
| Z1 | Z2 | Z3 | Z4 | Z5 | Z6 | Z7 | Z8 |
- When n is a prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
, groups of the form (Zn)m will have (nm-1)/(n-1) n-element cycles sharing the common identity element.
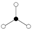 | 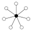 | 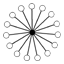 |  |
|---|---|---|---|
| Z2² | Z2³ | Z24 | Z3² |
- Dihedral groupDihedral groupIn mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
s Dihn consists of an n-element cycle and n 2-element cycles.
 |  |  | 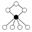 | 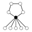 | 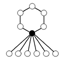 | 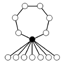 |
|---|---|---|---|---|---|---|
| Dih1 | Dih2 | Dih3 | Dih4 | Dih5 | Dih6 | Dih7 |
- Symmetric groupSymmetric groupIn mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
s - The symmetric group Sn contains, for any group of order n, a subgroup isomorphic to that group. Thus the cycle graph of every group of order n will be found as a subgraph of the cycle graph of Sn. See example: Subgroups of S4
External links
- http://mathworld.wolfram.com/CycleGraph.htmlCycle graph article on MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
]

