Cusp neighborhood
Encyclopedia
In mathematics
, a cusp neighborhood is defined as a set of points near a cusp
.
can be defined in terms of its Fuchsian model
.
Suppose that the Fuchsian group
G contains a parabolic element g. For example, the element t ∈ SL(2,Z) where
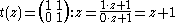
is a parabolic element. Note that all parabolic elements of SL(2,C) are conjugate
to this element. That is, if g ∈ SL(2,Z) is parabolic, then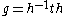
for some h ∈ SL(2,Z).
The set
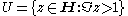
where H is the upper half-plane has
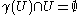
for any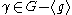
where 
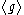is understood to mean the group
generated by g. That is, γ acts properly discontinuously on U. Because of this, it can be seen that the projection of U onto H/G is thus
.
Here, E is called the neighborhood of the cusp corresponding to g.
Note that the hyperbolic area of E is exactly 1, when computed using the canonical Poincaré metric
. This is most easily seen by example: consider the intersection of U defined above with the fundamental domain
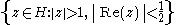
of the modular group
, as would be appropriate for the choice of T as the parabolic element. When integrated over the volume element
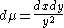
the result is trivially 1. Areas of all cusp neighborhoods are equal to this, by the invariance of the area under conjugation.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a cusp neighborhood is defined as a set of points near a cusp
Cusp (singularity)
In the mathematical theory of singularities a cusp is a type of singular point of a curve. Cusps are local singularities in that they are not formed by self intersection points of the curve....
.
Cusp neighborhood for a Riemann surface
The cusp neighborhood for a hyperbolic Riemann surfaceRiemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
can be defined in terms of its Fuchsian model
Fuchsian model
In mathematics, a Fuchsian model is a construction of a hyperbolic Riemann surface R as a quotient of the upper half-plane H. By the uniformization theorem, every Riemann surface is either elliptic, parabolic or hyperbolic. Every hyperbolic Riemann surface has a non-trivial fundamental group \pi_1...
.
Suppose that the Fuchsian group
Fuchsian group
In mathematics, a Fuchsian group is a discrete subgroup of PSL. The group PSL can be regarded as a group of isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations of the upper half plane, so a Fuchsian group can be regarded as a group acting...
G contains a parabolic element g. For example, the element t ∈ SL(2,Z) where
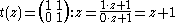
is a parabolic element. Note that all parabolic elements of SL(2,C) are conjugate
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
to this element. That is, if g ∈ SL(2,Z) is parabolic, then
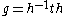for some h ∈ SL(2,Z).The set
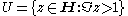
where H is the upper half-plane has
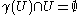
for any
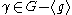where 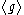is understood to mean the groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
generated by g. That is, γ acts properly discontinuously on U. Because of this, it can be seen that the projection of U onto H/G is thus
.Here, E is called the neighborhood of the cusp corresponding to g.
Note that the hyperbolic area of E is exactly 1, when computed using the canonical Poincaré metric
Poincaré metric
In mathematics, the Poincaré metric, named after Henri Poincaré, is the metric tensor describing a two-dimensional surface of constant negative curvature. It is the natural metric commonly used in a variety of calculations in hyperbolic geometry or Riemann surfaces.There are three equivalent...
. This is most easily seen by example: consider the intersection of U defined above with the fundamental domain
Fundamental domain
In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
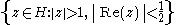
of the modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
, as would be appropriate for the choice of T as the parabolic element. When integrated over the volume element
Volume element
In mathematics, a volume element provides a means for integrating a function with respect to volume in various coordinate systems such as spherical coordinates and cylindrical coordinates...
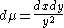
the result is trivially 1. Areas of all cusp neighborhoods are equal to this, by the invariance of the area under conjugation.