Curvelet
Encyclopedia
Curvelets are a non-adaptive
technique for multi-scale object
representation. Being an extension of the wavelet
concept, they are becoming popular in similar fields, namely in image processing
and scientific computing.
Wavelets generalize the Fourier transform
by using a basis that represents both location and spatial frequency. For 2D or 3D signals, directional wavelet transforms go further, by using basis functions that are also localized in orientation. A curvelet transform differs from other directional wavelet transforms in that the degree of localisation in orientation varies with scale. In particular, fine-scale basis functions are long ridges; the shape of the basis functions at scale j is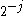
by 
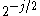so the fine-scale bases are skinny ridges with a precisely determined orientation.
Curvelets are an appropriate basis for representing images (or other functions) which are smooth apart from singularities along smooth curves, where the curves have bounded curvature, i.e. where objects in the image have a minimum length scale. This property holds for cartoons, geometrical diagrams, and text. As one zooms in on such images, the edges they contain appear increasingly straight. Curvelets take advantage of this property, by defining the higher resolution curvelets to be skinnier the lower resolution curvelets. However, natural images (photographs) do not have this property; they have detail at every scale. Therefore, for natural images, it is preferable to use some sort of directional wavelet transform whose wavelets have the same aspect ratio at every scale.
When the image is of the right type, curvelets provide a representation that is considerably sparser than other wavelet transforms. This can be quantified by considering the best approximation of a geometrical test image that can be represented using only
wavelets, and analysing the approximation error as a function of 
. For a Fourier transform, the error decreases only as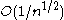 
. For a wide variety of wavelet transforms, including both directional and non-directional variants, the error decreases as 
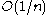. The extra assumption underlying the curvelet transform allows it to achieve 
.
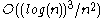Efficient numerical algorithms exist for computing the curvlet transform of discrete data. The computational cost of a curvlet transform is approximately 10–20 times that of an FFT, and has the same dependence of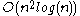
for an image of size 
.
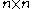Adaptive-additive algorithm
In the studies of Fourier optics, sound synthesis, stellar interferometry, optical tweezers, and diffractive optical elements it is often important to know the spatial frequency phase of an observed wave source. In order to reconstruct this phase the Adaptive-Additive Algorithm , which derives...
technique for multi-scale object
Object (computer science)
In computer science, an object is any entity that can be manipulated by the commands of a programming language, such as a value, variable, function, or data structure...
representation. Being an extension of the wavelet
Wavelet
A wavelet is a wave-like oscillation with an amplitude that starts out at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" like one might see recorded by a seismograph or heart monitor. Generally, wavelets are purposefully crafted to have...
concept, they are becoming popular in similar fields, namely in image processing
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
and scientific computing.
Wavelets generalize the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
by using a basis that represents both location and spatial frequency. For 2D or 3D signals, directional wavelet transforms go further, by using basis functions that are also localized in orientation. A curvelet transform differs from other directional wavelet transforms in that the degree of localisation in orientation varies with scale. In particular, fine-scale basis functions are long ridges; the shape of the basis functions at scale j is
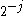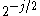by so the fine-scale bases are skinny ridges with a precisely determined orientation.Curvelets are an appropriate basis for representing images (or other functions) which are smooth apart from singularities along smooth curves, where the curves have bounded curvature, i.e. where objects in the image have a minimum length scale. This property holds for cartoons, geometrical diagrams, and text. As one zooms in on such images, the edges they contain appear increasingly straight. Curvelets take advantage of this property, by defining the higher resolution curvelets to be skinnier the lower resolution curvelets. However, natural images (photographs) do not have this property; they have detail at every scale. Therefore, for natural images, it is preferable to use some sort of directional wavelet transform whose wavelets have the same aspect ratio at every scale.
When the image is of the right type, curvelets provide a representation that is considerably sparser than other wavelet transforms. This can be quantified by considering the best approximation of a geometrical test image that can be represented using only
wavelets, and analysing the approximation error as a function of . For a Fourier transform, the error decreases only as 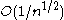. For a wide variety of wavelet transforms, including both directional and non-directional variants, the error decreases as 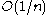. The extra assumption underlying the curvelet transform allows it to achieve 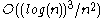.Efficient numerical algorithms exist for computing the curvlet transform of discrete data. The computational cost of a curvlet transform is approximately 10–20 times that of an FFT, and has the same dependence of
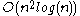for an image of size .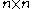