Cooley-Tukey FFT algorithm
Encyclopedia
The Cooley–Tukey algorithm
, named after J.W. Cooley
and John Tukey
, is the most common fast Fourier transform
(FFT) algorithm. It re-expresses the discrete Fourier transform
(DFT) of an arbitrary composite
size N = N1N2 in terms of smaller DFTs of sizes N1 and N2, recursively
, in order to reduce the computation time to O(N log N) for highly-composite N (smooth number
s). Because of the algorithm's importance, specific variants and implementation styles have become known by their own names, as described below.
Because the Cooley-Tukey algorithm breaks the DFT into smaller DFTs, it can be combined arbitrarily with any other algorithm for the DFT. For example, Rader's
or Bluestein's
algorithm can be used to handle large prime factors that cannot be decomposed by Cooley–Tukey, or the prime-factor algorithm
can be exploited for greater efficiency in separating out relatively prime factors.
See also the fast Fourier transform
for information on other FFT algorithms, specializations for real and/or symmetric data, and accuracy in the face of finite floating-point precision.
, who used it to interpolate the trajectories of the asteroid
s Pallas
and Juno
, but his work was not widely recognized (being published only posthumously and in neo-Latin
). Gauss did not analyze the asymptotic computational time, however. Various limited forms were also rediscovered several times throughout the 19th and early 20th centuries. FFTs became popular after J. W. Cooley of IBM and John W. Tukey
of Princeton
published a paper in 1965 reinventing the algorithm and describing how to perform it conveniently on a computer.
Tukey reportedly came up with the idea during a meeting of a US presidential advisory committee discussing ways to detect nuclear-weapon tests
in the Soviet Union
. Another participant at that meeting, Richard Garwin
of IBM, recognized the potential of the method and put Tukey in touch with Cooley, who implemented it for a different (and less-classified) problem: analyzing 3d crystallographic data (see also: multidimensional FFTs). Cooley and Tukey subsequently published their joint paper, and wide adoption quickly followed.
The fact that Gauss had described the same algorithm (albeit without analyzing its asymptotic cost) was not realized until several years after Cooley and Tukey's 1965 paper. Their paper cited as inspiration only work by I. J. Good on what is now called the prime-factor FFT algorithm
(PFA); although Good's algorithm was initially mistakenly thought to be equivalent to the Cooley–Tukey algorithm, it was quickly realized that PFA is a quite different algorithm (only working for sizes that have relatively prime factors and relying on the Chinese Remainder Theorem
, unlike the support for any composite size in Cooley–Tukey).
DFTs (hence the name "radix-2") of size N/2 with each recursive stage.
The discrete Fourier transform (DFT) is defined by the formula: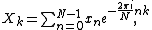
where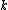
is an integer ranging from 
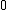to 
.
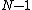Radix-2 DIT first computes the DFTs of the even-indexed inputs
(
)
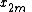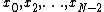and of the odd-indexed inputs
(
), and then combines those two results to produce the DFT of the whole sequence. This idea can then be performed recursively
to reduce the overall runtime to O(N log N). This simplified form assumes that N is a power of two
; since the number of sample points N can usually be chosen freely by the application, this is often not an important restriction.
The Radix-2 DIT algorithm rearranges the DFT of the function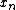
into two parts: a sum over the even-numbered indices 
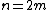and a sum over the odd-numbered indices 
:
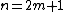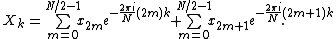
One can factor a common multiplier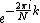
out of the second sum, as shown in the equation below. It is then clear that the two sums are the DFT of the even-indexed part 
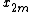and the DFT of odd-indexed part 
of the function 
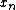. Denote the DFT of the Even-indexed inputs 
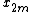by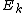 
and the DFT of the Odd-indexed inputs 
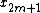by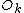 
and we obtain: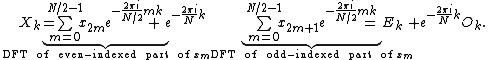
However, these smaller DFTs have a length of N/2, so we need compute only N/2 outputs: thanks to the periodicity properties of the DFT, the outputs for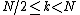
from a DFT of length N/2 are identical to the outputs for 
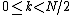. That is, 
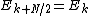and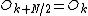 
. The phase factor 
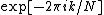(called a twiddle factor
) obeys the relation: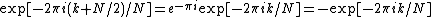
, flipping the sign of the 
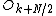terms. Thus, the whole DFT can be calculated as follows: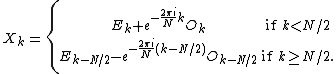
This result, expressing the DFT of length N recursively in terms of two DFTs of size N/2, is the core of the radix-2 DIT fast Fourier transform. The algorithm gains its speed by re-using the results of intermediate computations to compute multiple DFT outputs. Note that final outputs are obtained by a +/− combination of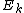
and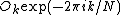 
, which is simply a size-2 DFT (sometimes called a butterfly
in this context); when this is generalized to larger radices below, the size-2 DFT is replaced by a larger DFT (which itself can be evaluated with an FFT).
This process is an example of the general technique of divide and conquer algorithm
s; in many traditional implementations, however, the explicit recursion is avoided, and instead one traverses the computational tree in breadth-first
fashion.
The above re-expression of a size-N DFT as two size-N/2 DFTs is sometimes called the Danielson–Lanczos
lemma
, since the identity was noted by those two authors in 1942 (influenced by Runge's 1903 work). They applied their lemma in a "backwards" recursive fashion, repeatedly doubling the DFT size until the transform spectrum converged (although they apparently didn't realize the linearithmic asymptotic complexity they had achieved). The Danielson–Lanczos work predated widespread availability of computer
s and required hand calculation (possibly with mechanical aids such as adding machine
s); they reported a computation time of 140 minutes for a size-64 DFT operating on real inputs to 3–5 significant digits. Cooley and Tukey's 1965 paper reported a running time of 0.02 minutes for a size-2048 complex DFT on an IBM 7094 (probably in 36-bit single precision
, ~8 digits). Rescaling the time by the number of operations, this corresponds roughly to a speedup factor of around 800,000. (To put the time for the hand calculation in perspective, 140 minutes for size 64 corresponds to an average of at most 16 seconds per floating-point operation, around 20% of which are multiplications.)
, the above process could be written:
X0,...,N−1 ← ditfft2(x, N, s): DFT of (x0, xs, x2s, ..., x(N-1)s):
if N = 1 then
X0 ← x0 trivial size-1 DFT base case
else
X0,...,N/2−1 ← ditfft2(x, N/2, 2s) DFT of (x0, x2s, x4s, ...)
XN/2,...,N−1 ← ditfft2(x+s, N/2, 2s) DFT of (xs, xs+2s, xs+4s, ...)
for k = 0 to N/2−1 combine DFTs of two halves into full DFT:
t ← Xk
Xk ← t + exp(−2πi k/N) Xk+N/2
Xk+N/2 ← t − exp(−2πi k/N) Xk+N/2
endfor
endif
Here,
of the input x array. x+s denotes the array starting with xs.
(The results are in the correct order in X and no further bit-reversal permutation
is required; the often-mentioned necessity of a separate bit-reversal stage only arises for certain in-place algorithms, as described below.)
High-performance FFT implementations make many modifications to the implementation of such an algorithm compared to this simple pseudocode. For example, one can use a larger base case than N=1 to amortize the overhead of recursion, the twiddle factors exp(−2πi k/N) can be precomputed, and larger radices are often used for cache
reasons; these and other optimizations together can improve the performance by an order of magnitude or more. (In many textbook implementations the depth-first recursion is eliminated entirely in favor of a nonrecursive breadth-first approach, although depth-first recursion has been argued to have better memory locality.) Several of these ideas are described in further detail below.
Typically, either N1 or N2 is a small factor (not necessarily prime), called the radix (which can differ between stages of the recursion). If N1 is the radix, it is called a decimation in time (DIT) algorithm, whereas if N2 is the radix, it is decimation in frequency (DIF, also called the Sande-Tukey algorithm). The version presented above was a radix-2 DIT algorithm; in the final expression, the phase multiplying the odd transform is the twiddle factor, and the +/- combination (butterfly) of the even and odd transforms is a size-2 DFT. (The radix's small DFT is sometimes known as a butterfly, so-called because of the shape of the dataflow diagram for the radix-2 case.)
There are many other variations on the Cooley–Tukey algorithm. Mixed-radix implementations handle composite sizes with a variety of (typically small) factors in addition to two, usually (but not always) employing the O(N2) algorithm for the prime base cases of the recursion[ it is also possible to employ an N log N algorithm for the prime base cases, such as Rader
's or Bluestein
's algorithm] . Split radix
merges radices 2 and 4, exploiting the fact that the first transform of radix 2 requires no twiddle factor, in order to achieve what was long the lowest known arithmetic operation count for power-of-two sizes, although recent variations achieve an even lower count. (On present-day computers, performance is determined more by cache
and CPU pipeline considerations than by strict operation counts; well-optimized FFT implementations often employ larger radices and/or hard-coded base-case transforms of significant size.) Another way of looking at the Cooley–Tukey algorithm is that it re-expresses a size N one-dimensional DFT as an N1 by N2 two-dimensional DFT (plus twiddles), where the output matrix is transpose
d. The net result of all of these transpositions, for a radix-2 algorithm, corresponds to a bit reversal of the input (DIF) or output (DIT) indices. If, instead of using a small radix, one employs a radix of roughly √N and explicit input/output matrix transpositions, it is called a four-step algorithm (or six-step, depending on the number of transpositions), initially proposed to improve memory locality, e.g. for cache optimization or out-of-core operation, and was later shown to be an optimal cache-oblivious algorithm.
The general Cooley–Tukey factorization rewrites the indices k and n as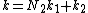
and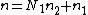 
, respectively, where the indices ka and na run from 0..Na-1 (for a of 1 or 2). That is, it re-indexes the input (n) and output (k) as N1 by N2 two-dimensional arrays in column-major and row-major order
, respectively; the difference between these indexings is a transposition, as mentioned above. When this re-indexing is substituted into the DFT formula for nk, the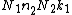
cross term vanishes (its exponential is unity), and the remaining terms give
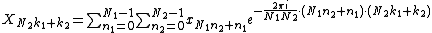
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
, named after J.W. Cooley
James Cooley
Dr. James W. Cooley is an American mathematician. James William Cooley received a B.A. degree in 1949 from Manhattan College, Bronx, NY, an M.A. degree in 1951 from Columbia University, New York, NY, and a Ph.D. degree in 1961 in applied mathematics from Columbia University...
and John Tukey
John Tukey
John Wilder Tukey ForMemRS was an American statistician.- Biography :Tukey was born in New Bedford, Massachusetts in 1915, and obtained a B.A. in 1936 and M.Sc. in 1937, in chemistry, from Brown University, before moving to Princeton University where he received a Ph.D...
, is the most common fast Fourier transform
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
(FFT) algorithm. It re-expresses the discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
(DFT) of an arbitrary composite
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
size N = N1N2 in terms of smaller DFTs of sizes N1 and N2, recursively
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
, in order to reduce the computation time to O(N log N) for highly-composite N (smooth number
Smooth number
In number theory, a smooth number is an integer which factors completely into small prime numbers. The term seems to have been coined by Leonard Adleman. Smooth numbers are especially important in cryptography relying on factorization.-Definition:...
s). Because of the algorithm's importance, specific variants and implementation styles have become known by their own names, as described below.
Because the Cooley-Tukey algorithm breaks the DFT into smaller DFTs, it can be combined arbitrarily with any other algorithm for the DFT. For example, Rader's
Rader's FFT algorithm
Rader's algorithm is a fast Fourier transform algorithm that computes the discrete Fourier transform of prime sizes by re-expressing the DFT as a cyclic convolution...
or Bluestein's
Bluestein's FFT algorithm
Bluestein's FFT algorithm , commonly called the chirp z-transform algorithm , is a fast Fourier transform algorithm that computes the discrete Fourier transform of arbitrary sizes by re-expressing the DFT as a convolution...
algorithm can be used to handle large prime factors that cannot be decomposed by Cooley–Tukey, or the prime-factor algorithm
Prime-factor FFT algorithm
The prime-factor algorithm , also called the Good–Thomas algorithm , is a fast Fourier transform algorithm that re-expresses the discrete Fourier transform of a size N = N1N2 as a two-dimensional N1×N2 DFT, but only for the case where N1 and N2 are relatively prime...
can be exploited for greater efficiency in separating out relatively prime factors.
See also the fast Fourier transform
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
for information on other FFT algorithms, specializations for real and/or symmetric data, and accuracy in the face of finite floating-point precision.
History
This algorithm, including its recursive application, was invented around 1805 by Carl Friedrich GaussCarl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
, who used it to interpolate the trajectories of the asteroid
Asteroid
Asteroids are a class of small Solar System bodies in orbit around the Sun. They have also been called planetoids, especially the larger ones...
s Pallas
2 Pallas
Pallas, formally designated 2 Pallas, is the second asteroid to have been discovered , and one of the largest. It is estimated to constitute 7% of the mass of the asteroid belt, and its diameter of 530–565 km is comparable to, or slightly larger than, that of 4 Vesta. It is however 20%...
and Juno
3 Juno
Juno , formal designation 3 Juno in the Minor Planet Center catalogue system, was the third asteroid to be discovered and is one of the larger main-belt asteroids, being one of the two largest stony asteroids, along with 15 Eunomia. Juno is estimated to contain 1% of the total mass of the asteroid...
, but his work was not widely recognized (being published only posthumously and in neo-Latin
New Latin
The term New Latin, or Neo-Latin, is used to describe the Latin language used in original works created between c. 1500 and c. 1900. Among other uses, Latin during this period was employed in scholarly and scientific publications...
). Gauss did not analyze the asymptotic computational time, however. Various limited forms were also rediscovered several times throughout the 19th and early 20th centuries. FFTs became popular after J. W. Cooley of IBM and John W. Tukey
John Tukey
John Wilder Tukey ForMemRS was an American statistician.- Biography :Tukey was born in New Bedford, Massachusetts in 1915, and obtained a B.A. in 1936 and M.Sc. in 1937, in chemistry, from Brown University, before moving to Princeton University where he received a Ph.D...
of Princeton
Princeton University
Princeton University is a private research university located in Princeton, New Jersey, United States. The school is one of the eight universities of the Ivy League, and is one of the nine Colonial Colleges founded before the American Revolution....
published a paper in 1965 reinventing the algorithm and describing how to perform it conveniently on a computer.
Tukey reportedly came up with the idea during a meeting of a US presidential advisory committee discussing ways to detect nuclear-weapon tests
Nuclear testing
Nuclear weapons tests are experiments carried out to determine the effectiveness, yield and explosive capability of nuclear weapons. Throughout the twentieth century, most nations that have developed nuclear weapons have tested them...
in the Soviet Union
Soviet Union
The Soviet Union , officially the Union of Soviet Socialist Republics , was a constitutionally socialist state that existed in Eurasia between 1922 and 1991....
. Another participant at that meeting, Richard Garwin
Richard Garwin
Richard Lawrence Garwin , is an American physicist. He received his bachelor's degree from the Case Institute of Technology in 1947 and obtained his Doctor of Philosophy from the University of Chicago in 1949, where he worked in the lab of Enrico Fermi.Garwin is IBM Fellow Emeritus at the Thomas J...
of IBM, recognized the potential of the method and put Tukey in touch with Cooley, who implemented it for a different (and less-classified) problem: analyzing 3d crystallographic data (see also: multidimensional FFTs). Cooley and Tukey subsequently published their joint paper, and wide adoption quickly followed.
The fact that Gauss had described the same algorithm (albeit without analyzing its asymptotic cost) was not realized until several years after Cooley and Tukey's 1965 paper. Their paper cited as inspiration only work by I. J. Good on what is now called the prime-factor FFT algorithm
Prime-factor FFT algorithm
The prime-factor algorithm , also called the Good–Thomas algorithm , is a fast Fourier transform algorithm that re-expresses the discrete Fourier transform of a size N = N1N2 as a two-dimensional N1×N2 DFT, but only for the case where N1 and N2 are relatively prime...
(PFA); although Good's algorithm was initially mistakenly thought to be equivalent to the Cooley–Tukey algorithm, it was quickly realized that PFA is a quite different algorithm (only working for sizes that have relatively prime factors and relying on the Chinese Remainder Theorem
Chinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
, unlike the support for any composite size in Cooley–Tukey).
The radix-2 DIT case
A radix-2 decimation-in-time (DIT) FFT is the simplest and most common form of the Cooley–Tukey algorithm, although highly optimized Cooley–Tukey implementations typically use other forms of the algorithm as described below. Radix-2 DIT divides a DFT of size N into two interleavedInterleaving
In computer science and telecommunication, interleaving is a way to arrange data in a non-contiguous way to increase performance.It is typically used:* In error-correction coding, particularly within data transmission, disk storage, and computer memory....
DFTs (hence the name "radix-2") of size N/2 with each recursive stage.
The discrete Fourier transform (DFT) is defined by the formula:
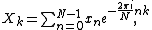
where
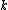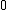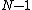is an integer ranging from to .Radix-2 DIT first computes the DFTs of the even-indexed inputs
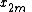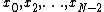()and of the odd-indexed inputs
(), and then combines those two results to produce the DFT of the whole sequence. This idea can then be performed recursivelyRecursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
to reduce the overall runtime to O(N log N). This simplified form assumes that N is a power of two
Power of two
In mathematics, a power of two means a number of the form 2n where n is an integer, i.e. the result of exponentiation with as base the number two and as exponent the integer n....
; since the number of sample points N can usually be chosen freely by the application, this is often not an important restriction.
The Radix-2 DIT algorithm rearranges the DFT of the function
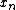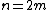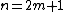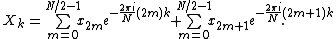
into two parts: a sum over the even-numbered indices and a sum over the odd-numbered indices :One can factor a common multiplier
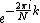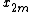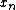out of the second sum, as shown in the equation below. It is then clear that the two sums are the DFT of the even-indexed part and the DFT of odd-indexed part of the function . Denote the DFT of the Even-indexed inputs 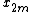by 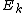and the DFT of the Odd-indexed inputs 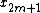by 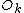and we obtain: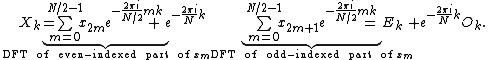However, these smaller DFTs have a length of N/2, so we need compute only N/2 outputs: thanks to the periodicity properties of the DFT, the outputs for
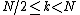from a DFT of length N/2 are identical to the outputs for 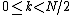. That is, 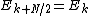and 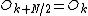. The phase factor 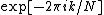(called a twiddle factorTwiddle factor
A twiddle factor, in fast Fourier transform algorithms, is any of the trigonometric constant coefficients that are multiplied by the data in the course of the algorithm...
) obeys the relation:
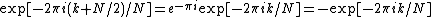, flipping the sign of the 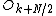terms. Thus, the whole DFT can be calculated as follows: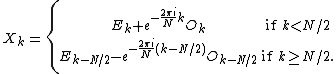This result, expressing the DFT of length N recursively in terms of two DFTs of size N/2, is the core of the radix-2 DIT fast Fourier transform. The algorithm gains its speed by re-using the results of intermediate computations to compute multiple DFT outputs. Note that final outputs are obtained by a +/− combination of
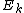and 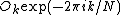, which is simply a size-2 DFT (sometimes called a butterflyButterfly diagram
In the context of fast Fourier transform algorithms, a butterfly is a portion of the computation that combines the results of smaller discrete Fourier transforms into a larger DFT, or vice versa . The name "butterfly" comes from the shape of the data-flow diagram in the radix-2 case, as described...
in this context); when this is generalized to larger radices below, the size-2 DFT is replaced by a larger DFT (which itself can be evaluated with an FFT).
This process is an example of the general technique of divide and conquer algorithm
Divide and conquer algorithm
In computer science, divide and conquer is an important algorithm design paradigm based on multi-branched recursion. A divide and conquer algorithm works by recursively breaking down a problem into two or more sub-problems of the same type, until these become simple enough to be solved directly...
s; in many traditional implementations, however, the explicit recursion is avoided, and instead one traverses the computational tree in breadth-first
Breadth-first search
In graph theory, breadth-first search is a graph search algorithm that begins at the root node and explores all the neighboring nodes...
fashion.
The above re-expression of a size-N DFT as two size-N/2 DFTs is sometimes called the Danielson–Lanczos
Cornelius Lanczos
Cornelius Lanczos Löwy Kornél was a Hungarian-Jewish mathematician and physicist, who was born on February 2, 1893, and died on June 25, 1974....
lemma
Lemma (mathematics)
In mathematics, a lemma is a proven proposition which is used as a stepping stone to a larger result rather than as a statement in-and-of itself...
, since the identity was noted by those two authors in 1942 (influenced by Runge's 1903 work). They applied their lemma in a "backwards" recursive fashion, repeatedly doubling the DFT size until the transform spectrum converged (although they apparently didn't realize the linearithmic asymptotic complexity they had achieved). The Danielson–Lanczos work predated widespread availability of computer
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
s and required hand calculation (possibly with mechanical aids such as adding machine
Adding machine
An adding machine was a class of mechanical calculator, usually specialized for bookkeeping calculations.In the United States, the earliest adding machines were usually built to read in dollars and cents. Adding machines were ubiquitous office equipment until they were phased out in favor of...
s); they reported a computation time of 140 minutes for a size-64 DFT operating on real inputs to 3–5 significant digits. Cooley and Tukey's 1965 paper reported a running time of 0.02 minutes for a size-2048 complex DFT on an IBM 7094 (probably in 36-bit single precision
Floating point
In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
, ~8 digits). Rescaling the time by the number of operations, this corresponds roughly to a speedup factor of around 800,000. (To put the time for the hand calculation in perspective, 140 minutes for size 64 corresponds to an average of at most 16 seconds per floating-point operation, around 20% of which are multiplications.)
Pseudocode
In pseudocodePseudocode
In computer science and numerical computation, pseudocode is a compact and informal high-level description of the operating principle of a computer program or other algorithm. It uses the structural conventions of a programming language, but is intended for human reading rather than machine reading...
, the above process could be written:
X0,...,N−1 ← ditfft2(x, N, s): DFT of (x0, xs, x2s, ..., x(N-1)s):
if N = 1 then
X0 ← x0 trivial size-1 DFT base case
else
X0,...,N/2−1 ← ditfft2(x, N/2, 2s) DFT of (x0, x2s, x4s, ...)
XN/2,...,N−1 ← ditfft2(x+s, N/2, 2s) DFT of (xs, xs+2s, xs+4s, ...)
for k = 0 to N/2−1 combine DFTs of two halves into full DFT:
t ← Xk
Xk ← t + exp(−2πi k/N) Xk+N/2
Xk+N/2 ← t − exp(−2πi k/N) Xk+N/2
endfor
endif
Here,
ditfft2(x,N,1), computes X=DFT(x) out-of-place by a radix-2 DIT FFT, where N is an integer power of 2 and s=1 is the strideStride of an array
In computer programming, the stride of an array refers to the number of locations in memory between successive array elements, measured in bytes or in units of the size of the array's elements....
of the input x array. x+s denotes the array starting with xs.
(The results are in the correct order in X and no further bit-reversal permutation
Bit-reversal permutation
In applied mathematics, a bit-reversal permutation is a permutation of a sequence with n = 2m elements, defined by reversing the binary digits of the index of each element...
is required; the often-mentioned necessity of a separate bit-reversal stage only arises for certain in-place algorithms, as described below.)
High-performance FFT implementations make many modifications to the implementation of such an algorithm compared to this simple pseudocode. For example, one can use a larger base case than N=1 to amortize the overhead of recursion, the twiddle factors exp(−2πi k/N) can be precomputed, and larger radices are often used for cache
Cache
In computer engineering, a cache is a component that transparently stores data so that future requests for that data can be served faster. The data that is stored within a cache might be values that have been computed earlier or duplicates of original values that are stored elsewhere...
reasons; these and other optimizations together can improve the performance by an order of magnitude or more. (In many textbook implementations the depth-first recursion is eliminated entirely in favor of a nonrecursive breadth-first approach, although depth-first recursion has been argued to have better memory locality.) Several of these ideas are described in further detail below.
General factorizations
More generally, Cooley–Tukey algorithms recursively re-express a DFT of a composite size N = N1N2 as:- Perform N1 DFTs of size N2.
- Multiply by complex roots of unity called twiddle factorTwiddle factorA twiddle factor, in fast Fourier transform algorithms, is any of the trigonometric constant coefficients that are multiplied by the data in the course of the algorithm...
s. - Perform N2 DFTs of size N1.
Typically, either N1 or N2 is a small factor (not necessarily prime), called the radix (which can differ between stages of the recursion). If N1 is the radix, it is called a decimation in time (DIT) algorithm, whereas if N2 is the radix, it is decimation in frequency (DIF, also called the Sande-Tukey algorithm). The version presented above was a radix-2 DIT algorithm; in the final expression, the phase multiplying the odd transform is the twiddle factor, and the +/- combination (butterfly) of the even and odd transforms is a size-2 DFT. (The radix's small DFT is sometimes known as a butterfly, so-called because of the shape of the dataflow diagram for the radix-2 case.)
There are many other variations on the Cooley–Tukey algorithm. Mixed-radix implementations handle composite sizes with a variety of (typically small) factors in addition to two, usually (but not always) employing the O(N2) algorithm for the prime base cases of the recursion
Rader's FFT algorithm
Rader's algorithm is a fast Fourier transform algorithm that computes the discrete Fourier transform of prime sizes by re-expressing the DFT as a cyclic convolution...
's or Bluestein
Bluestein's FFT algorithm
Bluestein's FFT algorithm , commonly called the chirp z-transform algorithm , is a fast Fourier transform algorithm that computes the discrete Fourier transform of arbitrary sizes by re-expressing the DFT as a convolution...
's algorithm
Split-radix FFT algorithm
The split-radix FFT is a fast Fourier transform algorithm for computing the discrete Fourier transform , and was first described in an initially little-appreciated paper by R. Yavne and subsequently rediscovered simultaneously by various authors in 1984. The split-radix FFT is a fast Fourier...
merges radices 2 and 4, exploiting the fact that the first transform of radix 2 requires no twiddle factor, in order to achieve what was long the lowest known arithmetic operation count for power-of-two sizes, although recent variations achieve an even lower count. (On present-day computers, performance is determined more by cache
CPU cache
A CPU cache is a cache used by the central processing unit of a computer to reduce the average time to access memory. The cache is a smaller, faster memory which stores copies of the data from the most frequently used main memory locations...
and CPU pipeline considerations than by strict operation counts; well-optimized FFT implementations often employ larger radices and/or hard-coded base-case transforms of significant size.) Another way of looking at the Cooley–Tukey algorithm is that it re-expresses a size N one-dimensional DFT as an N1 by N2 two-dimensional DFT (plus twiddles), where the output matrix is transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
d. The net result of all of these transpositions, for a radix-2 algorithm, corresponds to a bit reversal of the input (DIF) or output (DIT) indices. If, instead of using a small radix, one employs a radix of roughly √N and explicit input/output matrix transpositions, it is called a four-step algorithm (or six-step, depending on the number of transpositions), initially proposed to improve memory locality, e.g. for cache optimization or out-of-core operation, and was later shown to be an optimal cache-oblivious algorithm.
The general Cooley–Tukey factorization rewrites the indices k and n as
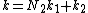and 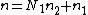, respectively, where the indices ka and na run from 0..Na-1 (for a of 1 or 2). That is, it re-indexes the input (n) and output (k) as N1 by N2 two-dimensional arrays in column-major and row-major orderRow-major order
In computing, row-major order and column-major order describe methods for storing multidimensional arrays in linear memory. Following standard matrix notation, rows are numbered by the first index of a two-dimensional array and columns by the second index. Array layout is critical for correctly...
, respectively; the difference between these indexings is a transposition, as mentioned above. When this re-indexing is substituted into the DFT formula for nk, the
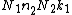cross term vanishes (its exponential is unity), and the remaining terms give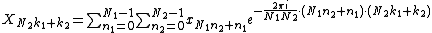
-
where each inner sum is a DFT of size N2, each outer sum is a DFT of size N1, and the[...] bracketed term is the twiddle factor.
An arbitrary radix r (as well as mixed radices) can be employed, as was shown by both Cooley and Tukey as well as Gauss (who gave examples of radix-3 and radix-6 steps). Cooley and Tukey originally assumed that the radix butterfly required O(r2) work and hence reckoned the complexity for a radix r to be O(r2 N/r logrN) = O(N log2(N) r/log2r); from calculation of values of r/log2r for integer values of r from 2 to 12 the optimal radix is found to be 3 (the closest integer to eE (mathematical constant)The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
, which minimizes r/log2r). This analysis was erroneous, however: the radix-butterfly is also a DFT and can be performed via an FFT algorithm in O(r log r) operations, hence the radix r actually cancels in the complexity O(r log(r) N/r logrN), and the optimal r is determined by more complicated considerations. In practice, quite large r (32 or 64) are important in order to effectively exploit e.g. the large number of processor registerProcessor registerIn computer architecture, a processor register is a small amount of storage available as part of a CPU or other digital processor. Such registers are addressed by mechanisms other than main memory and can be accessed more quickly...
s on modern processors, and even an unbounded radix r=√N also achieves O(N log N) complexity and has theoretical and practical advantages for large N as mentioned above.
Data reordering, bit reversal, and in-place algorithms
Although the abstract Cooley–Tukey factorization of the DFT, above, applies in some form to all implementations of the algorithm, much greater diversity exists in the techniques for ordering and accessing the data at each stage of the FFT. Of special interest is the problem of devising an in-place algorithmIn-place algorithmIn computer science, an in-place algorithm is an algorithm which transforms input using a data structure with a small, constant amount of extra storage space. The input is usually overwritten by the output as the algorithm executes...
that overwrites its input with its output data using only O(1) auxiliary storage.
The most well-known reordering technique involves explicit bit reversal for in-place radix-2 algorithms. Bit reversalBit-reversal permutationIn applied mathematics, a bit-reversal permutation is a permutation of a sequence with n = 2m elements, defined by reversing the binary digits of the index of each element...
is the permutationPermutationIn mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
where the data at an index n, written in binaryBinary numeral systemThe binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
with digits b4b3b2b1b0 (e.g. 5 digits for N=32 inputs), is transferred to the index with reversed digits b0b1b2b3b4 . Consider the last stage of a radix-2 DIT algorithm like the one presented above, where the output is written in-place over the input: when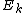
and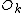 
are combined with a size-2 DFT, those two values are overwritten by the outputs. However, the two output values should go in the first and second halves of the output array, corresponding to the most significant bit b4 (for N=32); whereas the two inputs 
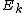and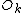 
are interleaved in the even and odd elements, corresponding to the least significant bit b0. Thus, in order to get the output in the correct place, these two bits must be swapped in the input. If you include all of the recursive stages of a radix-2 DIT algorithm, all the bits must be swapped and thus one must pre-process the input with a bit reversal to get in-order output. Correspondingly, the reversed (dual) algorithm is radix-2 DIF, and this takes in-order input and produces bit-reversed output, requiring a bit-reversal post-processing step. Alternatively, some applications (such as convolution) work equally well on bit-reversed data, so one can do radix-2 DIF without bit reversal, followed by processing, followed by the radix-2 DIT inverse DFT without bit reversal to produce final results in the natural order.
Many FFT users, however, prefer natural-order outputs, and a separate, explicit bit-reversal stage can have a non-negligible impact on the computation time, even though bit reversal can be done in O(N) time and has been the subject of much research. Also, while the permutation is a bit reversal in the radix-2 case, it is more generally an arbitrary (mixed-base) digit reversal for the mixed-radix case, and the permutation algorithms become more complicated to implement. Moreover, it is desirable on many hardware architectures to re-order intermediate stages of the FFT algorithm so that they operate on consecutive (or at least more localized) data elements. To these ends, a number of alternative implementation schemes have been devised for the Cooley–Tukey algorithm that do not require separate bit reversal and/or involve additional permutations at intermediate stages.
The problem is greatly simplified if it is out-of-place: the output array is distinct from the input array or, equivalently, an equal-size auxiliary array is available. The Stockham auto-sort algorithm performs every stage of the FFT out-of-place, typically writing back and forth between two arrays, transposing one "digit" of the indices with each stage, and has been especially popular on SIMDSIMDSingle instruction, multiple data , is a class of parallel computers in Flynn's taxonomy. It describes computers with multiple processing elements that perform the same operation on multiple data simultaneously...
architectures. Even greater potential SIMD advantages (more consecutive accesses) have been proposed for the Pease algorithm, which also reorders out-of-place with each stage, but this method requires separate bit/digit reversal and O(N log N) storage. One can also directly apply the Cooley–Tukey factorization definition with explicit (depth-firstDepth-first searchDepth-first search is an algorithm for traversing or searching a tree, tree structure, or graph. One starts at the root and explores as far as possible along each branch before backtracking....
) recursion and small radices, which produces natural-order out-of-place output with no separate permutation step (as in the pseudocode above) and can be argued to have cache-oblivious locality benefits on systems with hierarchical memoryCacheIn computer engineering, a cache is a component that transparently stores data so that future requests for that data can be served faster. The data that is stored within a cache might be values that have been computed earlier or duplicates of original values that are stored elsewhere...
.
A typical strategy for in-place algorithms without auxiliary storage and without separate digit-reversal passes involves small matrix transpositions (which swap individual pairs of digits) at intermediate stages, which can be combined with the radix butterflies to reduce the number of passes over the data.
External links
- a simple, pedagogical radix-2 Cooley–Tukey FFT algorithm in C++.
- KISSFFT: a simple mixed-radix Cooley–Tukey implementation in C (open source)