Convex lattice polytope
Encyclopedia
A convex lattice polytope (also called Z-polyhedron or Z-polytope) is a geometric
object playing an important role in discrete geometry
and combinatorial commutative algebra
. It is a polytope
in a Euclidean space Rn which is a convex hull
of finitely many points in the integer lattice
Zn ⊂ Rn. Such objects are prominently featured in the theory of toric varieties, where they correspond to polarized projective toric varieties.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
object playing an important role in discrete geometry
Discrete geometry
Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles,...
and combinatorial commutative algebra
Combinatorial commutative algebra
Combinatorial commutative algebra is a relatively new, rapidly developing mathematical discipline. As the name implies, it lies at the intersection of two more established fields, commutative algebra and combinatorics, and frequently uses methods of one to address problems arising in the other...
. It is a polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
in a Euclidean space Rn which is a convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of finitely many points in the integer lattice
Integer lattice
In mathematics, the n-dimensional integer lattice , denoted Zn, is the lattice in the Euclidean space Rn whose lattice points are n-tuples of integers. The two-dimensional integer lattice is also called the square lattice, or grid lattice. Zn is the simplest example of a root lattice...
Zn ⊂ Rn. Such objects are prominently featured in the theory of toric varieties, where they correspond to polarized projective toric varieties.
Examples
- An n-dimensional simplexSimplexIn geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
Δ in Rn is the convex hull of n+1 points that do not lie on a single affine hyperplane. The simplex is a convex lattice polytope if (and only if) the vertices have integral coordinates. The corresponding toric variety is the n-dimensional projective spaceProjective spaceIn mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
Pn. - The unit cubeUnit cubeA unit cube, sometimes called a cube of side 1, is a cube whose sides are 1 unit long. The volume of a 3-dimensional unit cube is 1 cubic unit, and its total surface area is 6 square units.- Unit Hypercube :...
in Rn, whose vertices are the 2n points all of whose coordinates are 0 or 1, is a convex lattice polytope. The corresponding toric variety is the Segre embeddingSegre embeddingIn mathematics, the Segre embedding is used in projective geometry to consider the cartesian product of two or more projective spaces as a projective variety...
of the n-fold product of the projective line P1. - In the special case of two-dimensional convex lattice polytopes in R2, they are also known as convex lattice polygons.
- In algebraic geometry, an important instance of lattice polytopes called the Newton polytopes are the convex hulls of the set
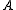which consists of all the exponent vectors appearing in a collection of monomials. For example, consider the polynomial of the form 
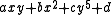with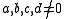 
has a lattice equal to the triangle
See also
- Normal polytopeNormal polytopeIn mathematics, specifically in combinatorial commutative algebra, a convex lattice polytope P is called normal if it has the following property: given any positive integer n, every lattice point of the dilation nP, obtained from P by scaling its vertices by the factor n and taking the convex hull...
- Pick's theoremPick's theoremGiven a simple polygon constructed on a grid of equal-distanced points such that all the polygon's vertices are grid points, Pick's theorem provides a simple formula for calculating the area A of this polygon in terms of the number i of lattice points in the interior located in the polygon and the...
- Ehrhart polynomialEhrhart polynomialIn mathematics, an integral polytope has an associated Ehrhart polynomial which encodes the relationship between the volume of a polytope and the number of integer points the polytope contains...
- Integer points in convex polyhedraInteger points in convex polyhedraStudy of integer points in convex polyhedra is motivated by the questions, such as "how many nonnegative integer-valued solutions does a system of linear equations with nonnegative coefficients have" or "how many solutions does an integer linear program have"...