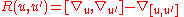Connection (algebraic framework)
Encyclopedia
Geometry of quantum systems
(e.g.,
noncommutative geometry
and supergeometry
) is mainly
phrased in algebraic terms of modules
and
algebras. Connections on modules are
generalization of a linear connection
on a smooth vector bundle
 written as a Koszul connection on the
written as a Koszul connection on the
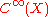 -module of sections of
-module of sections of  .
.
 be a commutative ring
be a commutative ring
and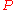 a
a  -module
-module
. There are different equivalent definitions
of a connection on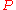 . Let
. Let 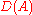 be the module of derivations
be the module of derivations
of a ring . A
. A
connection on an -module
-module 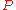 is defined
is defined
as an -module morphism
-module morphism
such that the first order differential operator
s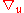 on
on
 obey the Leibniz rule
obey the Leibniz rule
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
(e.g.,
noncommutative geometry
Noncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
and supergeometry
Supergeometry
Supergeometry is differential geometry of modules over graded commutative algebras, supermanifolds and graded manifolds. Supergeometry is part and parcel of many classical and quantum field theories involving odd fields, e.g., SUSY field theory, BRST theory, or supergravity.Supergeometry is...
) is mainly
phrased in algebraic terms of modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
and
algebras. Connections on modules are
generalization of a linear connection
Connection (vector bundle)
In mathematics, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. If the fiber bundle is a vector bundle, then the notion of parallel transport is required to be linear...
on a smooth vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
 written as a Koszul connection on the
written as a Koszul connection on the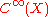 -module of sections of
-module of sections of  .
.Commutative algebra
Let be a commutative ring
be a commutative ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
and
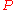 a
a  -module
-moduleModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
. There are different equivalent definitions
of a connection on
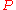 . Let
. Let 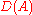 be the module of derivations
be the module of derivationsDerivation (abstract algebra)
In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
of a ring
 . A
. Aconnection on an
 -module
-module 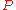 is defined
is definedas an
 -module morphism
-module morphismsuch that the first order differential operator
Differential calculus over commutative algebras
In mathematics the differential calculus over commutative algebras is a part of commutative algebra based on the observation that most concepts known from classical differential calculus can be formulated in purely algebraic terms...
s
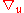 on
on obey the Leibniz rule
obey the Leibniz rule-
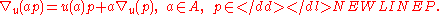
Connections on a module over a commutative ring always exist.
The curvature of the connection is defined as
is defined as
the zero-order differential operator
on the module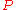 for all
for all 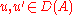 .
.
If is a vector bundle, there is one-to-one
is a vector bundle, there is one-to-one
correspondence between linear
connectionsConnection (vector bundle)In mathematics, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. If the fiber bundle is a vector bundle, then the notion of parallel transport is required to be linear...
 on
on  and the
and the
connections on the
on the
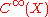 -module of sections of
-module of sections of  . Strictly speaking,
. Strictly speaking,  corresponds to
corresponds to
the covariant differentialCovariant derivativeIn mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
of a
connection on .
.
Graded commutative algebra
The notion of a connection on modules over commutative rings is
straightforwardly extended to modules over a graded
commutative algebraSuperalgebraIn mathematics and theoretical physics, a superalgebra is a Z2-graded algebra. That is, it is an algebra over a commutative ring or field with a decomposition into "even" and "odd" pieces and a multiplication operator that respects the grading....
. This is the case of
superconnectionsSupergeometrySupergeometry is differential geometry of modules over graded commutative algebras, supermanifolds and graded manifolds. Supergeometry is part and parcel of many classical and quantum field theories involving odd fields, e.g., SUSY field theory, BRST theory, or supergravity.Supergeometry is...
in supergeometrySupergeometrySupergeometry is differential geometry of modules over graded commutative algebras, supermanifolds and graded manifolds. Supergeometry is part and parcel of many classical and quantum field theories involving odd fields, e.g., SUSY field theory, BRST theory, or supergravity.Supergeometry is...
of
graded manifoldGraded manifoldGraded manifolds are extensions of the manifold concept based on ideas coming from supersymmetry and supercommutative algebra. Graded manifolds are not supermanifolds though there is a certain correspondence between the graded manifolds and the DeWitt supermanifolds. Both graded manifolds and...
s and supervector bundlesSupergeometrySupergeometry is differential geometry of modules over graded commutative algebras, supermanifolds and graded manifolds. Supergeometry is part and parcel of many classical and quantum field theories involving odd fields, e.g., SUSY field theory, BRST theory, or supergravity.Supergeometry is...
.
Superconnections always exist.
Noncommutative algebra
If is a noncommutative ring, connections on left
is a noncommutative ring, connections on left
and right -modules are defined similarly to those on
-modules are defined similarly to those on
modules over commutative rings. However
these connections need not exist.
In contrast with connections on left and right modules, there is a
problem how to define a connection on an
 -bimoduleBimoduleIn abstract algebra a bimodule is an abelian group that is both a left and a right module, such that the left and right multiplications are compatible...
-bimoduleBimoduleIn abstract algebra a bimodule is an abelian group that is both a left and a right module, such that the left and right multiplications are compatible...
over noncommutative rings
 and
and 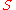 . There are different definitions
. There are different definitions
of such a connection. Let us mention one of them. A connection on an
 -bimodule
-bimodule 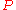 is defined as a bimodule
is defined as a bimodule
morphism
which obeys the Leibniz rule
-
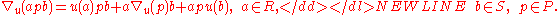
See also
- Connection (vector bundle)Connection (vector bundle)In mathematics, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. If the fiber bundle is a vector bundle, then the notion of parallel transport is required to be linear...
- Noncommutative geometryNoncommutative geometryNoncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
- SupergeometrySupergeometrySupergeometry is differential geometry of modules over graded commutative algebras, supermanifolds and graded manifolds. Supergeometry is part and parcel of many classical and quantum field theories involving odd fields, e.g., SUSY field theory, BRST theory, or supergravity.Supergeometry is...
- Differential calculus over commutative algebrasDifferential calculus over commutative algebrasIn mathematics the differential calculus over commutative algebras is a part of commutative algebra based on the observation that most concepts known from classical differential calculus can be formulated in purely algebraic terms...
External links
- Sardanashvily, G.Gennadi SardanashvilyGennadi Sardanashvily is a theoretical physicist, a principal research scientist of Moscow State University.- Biography :...
, Lectures on differential geometry of modules and rings, arXiv: 0910.1515
- Connection (vector bundle)
-