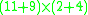.gif)
Confluence (abstract rewriting)
Encyclopedia
In computer science, confluence is a property of rewriting
systems, describing that terms in this system can be rewritten in more than one way, to yield the same result. This article describes the properties in the most abstract setting of an abstract rewriting system
.
We can rewrite this expression in two ways—either simplifying the first bracket, or the second. Simplifying the first bracket, we have
Simplifying the second, gives
We get the same result from rewriting the term in two different ways. This suggests that the rewriting system formed from regular arithmetic is a confluent rewriting system.
 A rewriting system can be expressed as a directed graph in which nodes represent expressions and edges represent rewrites. So, for example, if the expression
A rewriting system can be expressed as a directed graph in which nodes represent expressions and edges represent rewrites. So, for example, if the expression  can be rewritten into
can be rewritten into  , then we say that
, then we say that  is a reduct of
is a reduct of  (alternatively,
(alternatively,  reduces to
reduces to 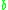 , or
, or 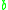 is an expansion of
is an expansion of  ). This is represented using arrow notation;
). This is represented using arrow notation; 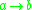 indicates that
indicates that  reduces to
reduces to 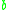 . Intuitively, this means that the corresponding graph has a directed edge from
. Intuitively, this means that the corresponding graph has a directed edge from  to
to 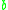 .
.
If there is a path between two graph nodes (let's call them and
and  ), then the intermediate nodes form a reduction sequence. So, for instance, if
), then the intermediate nodes form a reduction sequence. So, for instance, if 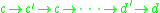 , then we can write
, then we can write 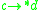 , indicating the existence of a reduction sequence from
, indicating the existence of a reduction sequence from  to
to 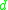 .
.
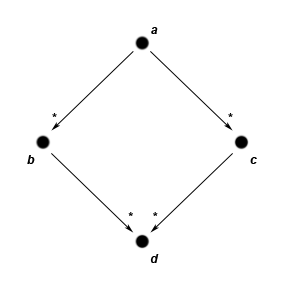
With this established, confluence can be defined as follows. Let a, b, c ∈ S, with a →* b and a →* c. a is deemed confluent if there exists a d ∈ S with b →* d and c →* d. If every a ∈ S is confluent, we say that → is confluent, or has the Church-Rosser property. This property is also sometimes called the diamond property, after the shape of the diagram shown on the right. Caution: other presentations reserve the term diamond property for a variant of the diagram with single reductions everywhere; that is, whenever a → b and a → c, there must exist a d such that b → d and c → d. The single-reduction variant is strictly stronger than the multi-reduction one.
We may view →*, which we introduced as a notation for reduction sequences, as a rewriting system in its own right, whose relation is the transitive closure
of R. Since a sequence of reduction sequences is again a reduction sequence (or, equivalently, since forming the transitive closure is idempotent), →** = →*. It follows that → is confluent if and only if →* is locally confluent.
A rewriting system may be locally confluent without being globally confluent. However, Newman's lemma
states that if a locally confluent rewriting system has no infinite reduction sequences (in which case it is said to be terminating or strongly normalizing), then it is globally confluent.
A semi-confluent element need not be confluent, but a semi-confluent rewriting system is necessarily confluent.
A strongly confluent element need not be confluent, but a strongly confluent rewriting system is necessarily confluent.
Rewriting
In mathematics, computer science, and logic, rewriting covers a wide range of methods of replacing subterms of a formula with other terms. What is considered are rewriting systems...
systems, describing that terms in this system can be rewritten in more than one way, to yield the same result. This article describes the properties in the most abstract setting of an abstract rewriting system
Abstract rewriting system
In mathematical logic and theoretical computer science, an abstract rewriting system is a formalism that captures the quintessential notion and properties of rewriting systems...
.
Motivating example
Consider the rules of regular arithmetic. We can think of these rules as forming a rewriting system. Suppose we are given the expressionWe can rewrite this expression in two ways—either simplifying the first bracket, or the second. Simplifying the first bracket, we have
Simplifying the second, gives
We get the same result from rewriting the term in two different ways. This suggests that the rewriting system formed from regular arithmetic is a confluent rewriting system.
General case and theory

 can be rewritten into
can be rewritten into 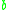 , then we say that
, then we say that 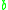 is a reduct of
is a reduct of  (alternatively,
(alternatively,  reduces to
reduces to 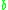 , or
, or 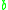 is an expansion of
is an expansion of  ). This is represented using arrow notation;
). This is represented using arrow notation; 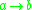 indicates that
indicates that  reduces to
reduces to 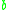 . Intuitively, this means that the corresponding graph has a directed edge from
. Intuitively, this means that the corresponding graph has a directed edge from  to
to 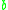 .
.If there is a path between two graph nodes (let's call them
 and
and  ), then the intermediate nodes form a reduction sequence. So, for instance, if
), then the intermediate nodes form a reduction sequence. So, for instance, if 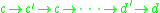 , then we can write
, then we can write 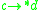 , indicating the existence of a reduction sequence from
, indicating the existence of a reduction sequence from  to
to 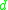 .
.With this established, confluence can be defined as follows. Let a, b, c ∈ S, with a →* b and a →* c. a is deemed confluent if there exists a d ∈ S with b →* d and c →* d. If every a ∈ S is confluent, we say that → is confluent, or has the Church-Rosser property. This property is also sometimes called the diamond property, after the shape of the diagram shown on the right. Caution: other presentations reserve the term diamond property for a variant of the diagram with single reductions everywhere; that is, whenever a → b and a → c, there must exist a d such that b → d and c → d. The single-reduction variant is strictly stronger than the multi-reduction one.
Local confluence
An element a ∈ S is said to be locally (or weakly) confluent if for all b, c ∈ S with a → b and a → c there exists d ∈ S with b →* d and c →* d. If every a ∈ S is locally confluent, we say that → is locally (or weakly) confluent, or has the weak Church-Rosser property. This is different from confluence in that b and c must be reduced from a in one step. In analogy with this, confluence is sometimes referred to as global confluence.We may view →*, which we introduced as a notation for reduction sequences, as a rewriting system in its own right, whose relation is the transitive closure
Transitive closure
In mathematics, the transitive closure of a binary relation R on a set X is the transitive relation R+ on set X such that R+ contains R and R+ is minimal . If the binary relation itself is transitive, then the transitive closure will be that same binary relation; otherwise, the transitive closure...
of R. Since a sequence of reduction sequences is again a reduction sequence (or, equivalently, since forming the transitive closure is idempotent), →** = →*. It follows that → is confluent if and only if →* is locally confluent.
A rewriting system may be locally confluent without being globally confluent. However, Newman's lemma
Newman's lemma
In the theory of rewriting systems, Newman's lemma states that a terminating abstract rewriting system , that is, one in which there are no infinite reduction sequences, is confluent if it is locally confluent...
states that if a locally confluent rewriting system has no infinite reduction sequences (in which case it is said to be terminating or strongly normalizing), then it is globally confluent.
Semi-confluence
The definition of local confluence differs from that of global confluence in that only elements reached from a given element in a single rewriting step are considered. By considering one element reached in a single step and another element reached by an arbitrary sequence, we arrive at the intermediate concept of semi-confluence: a ∈ S is said to be semi-confluent if for all b, c ∈ S with a → b and a →* c there exists d ∈ S with b →* d and c →* d; if every a ∈ S is semi-confluent, we say that → is semi-confluent.A semi-confluent element need not be confluent, but a semi-confluent rewriting system is necessarily confluent.
Strong confluence
Strong confluence is another variation on local confluence that allows us to conclude that a rewriting system is globally confluent. An element a ∈ S is said to be strongly confluent if for all b, c ∈ S with a → b and a → c there exists d ∈ S with b →* d and either c → d or c = d; if every a ∈ S is strongly confluent, we say that → is strongly confluent.A strongly confluent element need not be confluent, but a strongly confluent rewriting system is necessarily confluent.