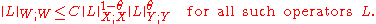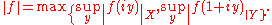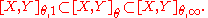Complex interpolation
Encyclopedia
In the field of mathematical analysis
, an interpolation space is a space which lies "in between" two other spaces. The main applications are in Sobolev space
s, where spaces of functions that have a noninteger number of derivative
s are interpolated from the spaces of functions with integer number of derivatives.
, later generalized and now known as the Riesz-Thorin theorem
. In simple terms, if a linear function is continuous on a certain space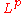
and also on a certain space 
, then it is also continuous on the space 
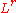, for any intermediate r between p and q. In other words, 
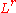is a space which is intermediate, or between 
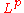and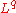 
.
In the development of Sobolev spaces, it became clear that the trace spaces were not any of the usual function spaces (with integer number of derivatives), and Jacques-Louis Lions
discovered that indeed these trace spaces were constituted of functions that have a noninteger degree of differentiability.
Many methods were designed to generate such spaces of functions, including the Fourier transform
, complex interpolation, real interpolation, as well as other tools (see e.g. fractional derivative).
s. In this article, we are interested in the following situation. X and Z are Banach spaces, and X is a subset of Z, but the norm
of X is not the same as the one of Z. An example of this can be obtained by taking X to be the Sobolev space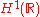
and by taking Z to be 
. We say that X is continuously included in Z when we have there is a constant 
such that
This is the case of the example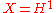
and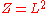 
.
Assume that we are given Banach spaces X and Y, and that they are both subsets of Z. Further define norms on
and 
by
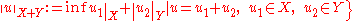
The following inclusions are all continuous:
(The space Z plays no further role, it was merely a tool that allows us to make sense of X+Y.) Our interest now is to come up with "intermediate spaces", between X and Y in the following sense:
We have used the notation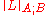
to denote the norm of the operator L as a map from A to B. If C=1 (which is the smallest possible), we further say that W is an exact interpolation space.
There are many ways of obtaining interpolation spaces (and the Riesz-Thorin theorem
is an example of this for Lp spaces). A method for arbitrary Banach spaces is the complex interpolation method.
of scalars is the complex number
s, then we may use properties of complex analytic function
s to define an interpolation space.
It is then easy to show that we have the
s.
Then,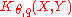
is an exact interpolation space of power θ.
Again,
is an exact interpolation space of power θ.
When the two methods are equivalent, we write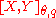
for the real interpolation method. By contrast, the complex interpolation method is usually not equivalent to the real interpolation method. However, there is still a relationship.
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, an interpolation space is a space which lies "in between" two other spaces. The main applications are in Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
s, where spaces of functions that have a noninteger number of derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s are interpolated from the spaces of functions with integer number of derivatives.
History
The theory of interpolation of vector spaces began by an observation of Józef MarcinkiewiczJózef Marcinkiewicz
Józef Marcinkiewicz – died in 1940 in Kharkiv, Ukraine) was a Polish mathematician.He was a student of Antoni Zygmund; and later worked with Juliusz Schauder, and Stefan Kaczmarz. He was a professor of the Stefan Batory University in Wilno....
, later generalized and now known as the Riesz-Thorin theorem
Riesz-Thorin theorem
In mathematics, the Riesz–Thorin theorem, often referred to as the Riesz–Thorin interpolation theorem or the Riesz–Thorin convexity theorem is a result about interpolation of operators. It is named after Marcel Riesz and his student G. Olof Thorin.This theorem bounds the norms of linear maps...
. In simple terms, if a linear function is continuous on a certain space
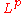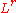and also on a certain space , then it is also continuous on the space , for any intermediate r between p and q. In other words, 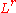is a space which is intermediate, or between 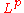and 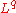.In the development of Sobolev spaces, it became clear that the trace spaces were not any of the usual function spaces (with integer number of derivatives), and Jacques-Louis Lions
Jacques-Louis Lions
Jacques-Louis Lions ForMemRS was a French mathematician who made contributions to the theory of partial differential equations and to stochastic control, among other areas. He received the SIAM's John Von Neumann prize in 1986. Lions is listed as an ISI highly cited researcher.-Biography:After...
discovered that indeed these trace spaces were constituted of functions that have a noninteger degree of differentiability.
Many methods were designed to generate such spaces of functions, including the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
, complex interpolation, real interpolation, as well as other tools (see e.g. fractional derivative).
Technical discussion
In order to discuss some of the main results of the theory, it is necessary for the reader to have some familiarity with the theory of Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s. In this article, we are interested in the following situation. X and Z are Banach spaces, and X is a subset of Z, but the norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
of X is not the same as the one of Z. An example of this can be obtained by taking X to be the Sobolev space
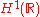and by taking Z to be . We say that X is continuously included in Z when we have there is a constant such thatThis is the case of the example
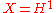and 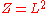.Assume that we are given Banach spaces X and Y, and that they are both subsets of Z. Further define norms on
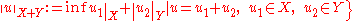
and byThe following inclusions are all continuous:
(The space Z plays no further role, it was merely a tool that allows us to make sense of X+Y.) Our interest now is to come up with "intermediate spaces", between X and Y in the following sense:
- Definition: With X and Y as above, an interpolation space is a Banach space W with the following property:
- If L is a linear operator from X+Y into itself, which is continuous from X into itself and from Y into itself, then it is also continuous from W into itself.
- The space W is further said to be of exponent θ (with 0<θ<1) if there exists a constant C such that
We have used the notation
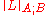to denote the norm of the operator L as a map from A to B. If C=1 (which is the smallest possible), we further say that W is an exact interpolation space.There are many ways of obtaining interpolation spaces (and the Riesz-Thorin theorem
Riesz-Thorin theorem
In mathematics, the Riesz–Thorin theorem, often referred to as the Riesz–Thorin interpolation theorem or the Riesz–Thorin convexity theorem is a result about interpolation of operators. It is named after Marcel Riesz and his student G. Olof Thorin.This theorem bounds the norms of linear maps...
is an example of this for Lp spaces). A method for arbitrary Banach spaces is the complex interpolation method.
Complex interpolation
If the fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of scalars is the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, then we may use properties of complex analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s to define an interpolation space.
- Definition: For two Banach spaces X and Y, the complex interpolation method consists in looking at the space of analytic functions f with values in X+Y, defined on the open strip
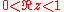, and continuous on the closed strip 
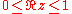, and such that
- f(iy) is bounded in X, f(1+iy) is bounded in Y.
- We define the norm
- For 0 < θ < 1, one defines
It is then easy to show that we have the
- Theorem: W = [X, Y]θ is an exact interpolation space of exponent θ.
Real interpolation (the K-method)
The K-method of real interpolation can be used even when the field of scalars is the real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s.
- Definition: For any
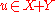, let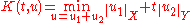 
and let
- Then, the K-method of real interpolation consists in taking
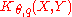to be the set of all u in X+Y such that 
.
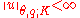Then,
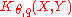is an exact interpolation space of power θ.Real interpolation (the J-method)
As with the K-method, the J-method can also be used for vector spaces over the real numbers.- Definition: For any
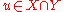, let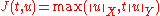 
. Then, u is in 
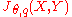if and only if it can be written as 
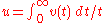, where v(t) is measurable with values in 
, and such that
- The norm of u is
.
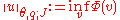Again,
is an exact interpolation space of power θ.Relations between the interpolation methods
The two real interpolation methods are often equivalent.- Theorem: If 0<θ<1 and 1 ≤ q ≤ ∞, then
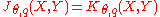with equivalence of norms.
When the two methods are equivalent, we write
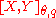for the real interpolation method. By contrast, the complex interpolation method is usually not equivalent to the real interpolation method. However, there is still a relationship.- Theorem: If 0 < θ < 1, then
