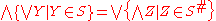Completely distributive lattice
Encyclopedia
In the mathematical area of order theory
, a completely distributive lattice is a complete lattice
in which arbitrary joins distribute
over arbitrary meets.
Formally, a complete lattice L is said to be completely distributive if, for any doubly indexed family
{xj,k | j in J, k in Kj} of L, we have
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
, a completely distributive lattice is a complete lattice
Complete lattice
In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...
in which arbitrary joins distribute
Distributivity (order theory)
In the mathematical area of order theory, there are various notions of the common concept of distributivity, applied to the formation of suprema and infima...
over arbitrary meets.
Formally, a complete lattice L is said to be completely distributive if, for any doubly indexed family
{xj,k | j in J, k in Kj} of L, we have
-
where F is the set of choice functions f choosing for each index j of J some index f(j) in Kj.
Complete distributivity is a self-dual property, i.e. dualizingDuality (order theory)In the mathematical area of order theory, every partially ordered set P gives rise to a dual partially ordered set which is often denoted by Pop or Pd. This dual order Pop is defined to be the set with the inverse order, i.e. x ≤ y holds in Pop if and only if y ≤ x holds in P...
the above statement yields the same class of complete lattices.
Alternative characterizations
Various different characterizations exist. For example, the following is an equivalent law that avoids the use of choice functions. For any set S of sets, we define the set S# to be the set of all subsets X of the complete lattice that have non-empty intersection with all members of S. We then can define complete distributivity via the statement
The operator # might be called the crosscut operator. This version of complete distributivity only implies the original notion when admitting the Axiom of Choice.
Properties
In addition, it is known that the following statements are equivalent for any complete lattice L:
- L is completely distributive.
- L can be embedded into a direct product of chains [0,1] by an order embedding that preserves arbitrary meets and joins.
- Both L and its dual order Lop are continuous posets.
Direct products of [0,1], i.e. sets of all functions from some set X to [0,1] ordered pointwise, are also called cubes.
Free completely distributive lattices
Every posetPartially ordered setIn mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
C can be completed in a completely distributive lattice.
A completely distributive lattice L is called the free completely distributive lattice over a poset C if and only if there is an order embedding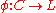
such that for every completely distributive lattice M and monotonic functionMonotonic functionIn mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
, there is a unique complete homomorphism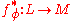 
satisfying 
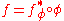. For every poset C, the free completely distributive lattice over a poset C exists and is unique up to isomorphism.
This is an instance of the concept of free objectFree objectIn mathematics, the idea of a free object is one of the basic concepts of abstract algebra. It is a part of universal algebra, in the sense that it relates to all types of algebraic structure . It also has a formulation in terms of category theory, although this is in yet more abstract terms....
. Since a set X can be considered as a poset with the discrete order, the above result guarantees the existence of the free completely distributive lattice over the set X.
Examples
- The unit intervalUnit intervalIn mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
[0,1], ordered in the natural way, is a completely distributive lattice.- More generally, any complete chain is a completely distributive lattice.
- The power set lattice
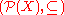for any set X is a completely distributive lattice. - For every poset C, there is a free completely distributive lattice over C. See the section on Free completely distributive lattices above.
-
