
Compact quantum group
Encyclopedia
In mathematics
, a compact quantum group is an abstract structure on a unital separable C*-algebra axiomatized from those that exist on the commutative C*-algebra of "continuous complex-valued functions" on a compact quantum group.
The basic motivation for this theory comes from the following analogy. The space of complex-valued functions on a compact Hausdorff topological space forms a commutative C*-algebra. On the other hand, by the Gelfand Theorem
, a commutative C*-algebra is isomorphic to the C*-algebra of continuous complex-valued functions on a compact Hausdorff topological space, and the topological space is uniquely determined by the C*-algebra up to homeomorphism
.
S. L. Woronowicz
introduced the important concept of compact matrix quantum groups, which he initially called compact pseudogroups. Compact matrix quantum groups are abstract structures on which the "continuous functions" on the structure are given by elements of a C*-algebra. The geometry of a compact matrix quantum group is a special case of a noncommutative geometry
.
, , there exists a C*-algebra homomorphism
, there exists a C*-algebra homomorphism
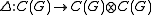
where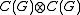 is the minimal C*-algebra tensor product — the completion of the algebraic tensor product
is the minimal C*-algebra tensor product — the completion of the algebraic tensor product
of and
and 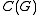 ) — such that
) — such that
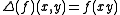
for all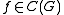 , and for all
, and for all 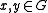 , where
, where
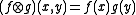
for all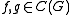 and all
and all 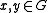 . There also exists a linear multiplicative mapping
. There also exists a linear multiplicative mapping
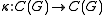 ,
,
such that

for all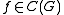 and all
and all 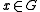 . Strictly speaking, this does not make
. Strictly speaking, this does not make 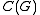 into a Hopf algebra
into a Hopf algebra
, unless is finite.
is finite.
On the other hand, a finite-dimensional representation
of G can be used to generate a *-subalgebra of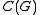 which is also a Hopf *-algebra. Specifically, if
which is also a Hopf *-algebra. Specifically, if
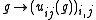
is an -dimensional representation
-dimensional representation
of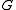 , then
, then
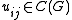
for all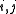 , and
, and
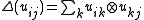
for all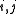 . It follows that the *-algebra generated by
. It follows that the *-algebra generated by 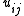 for all
for all 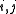 and
and 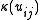 for all
for all 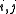 is a Hopf *-algebra: the counit is determined by
is a Hopf *-algebra: the counit is determined by
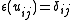
for all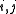 (where
(where 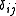 is the Kronecker delta), the antipode is
is the Kronecker delta), the antipode is  , and the unit is given by
, and the unit is given by

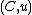 , where
, where 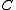 is a C*-algebra and
is a C*-algebra and
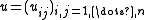
is a matrix with entries in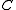 such that
such that
As a consequence of continuity, the comultiplication on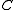 is coassociative.
is coassociative.
In general,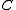 is a bialgebra, and
is a bialgebra, and 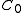 is a Hopf *-algebra.
is a Hopf *-algebra.
Informally,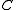 can be regarded as the *-algebra of continuous complex-valued functions over the compact matrix quantum group, and
can be regarded as the *-algebra of continuous complex-valued functions over the compact matrix quantum group, and  can be regarded as a finite-dimensional representation of the compact matrix quantum group.
can be regarded as a finite-dimensional representation of the compact matrix quantum group.
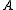 and
and 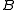 acting on the Hilbert spaces
acting on the Hilbert spaces 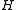 and
and 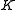 respectively, their minimal tensor product is defined to be the norm completion of the algebraic tensor product
respectively, their minimal tensor product is defined to be the norm completion of the algebraic tensor product 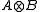 in
in 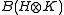 ; the norm completion is also denoted by
; the norm completion is also denoted by 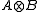 .
.
A compact quantum group is defined as a pair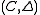 , where
, where 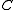 is a unital separable C*-algebra and
is a unital separable C*-algebra and
of the Hopf *-algebra (a corepresentation of a counital coassiative coalgebra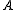 is a square matrix
is a square matrix
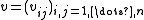
with entries in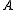 (so
(so  ) such that
) such that
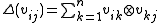
for all and
and
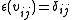 for all
for all  ). Furthermore, a representation, v, is called unitary if the matrix for v is unitary, or equivalently, if
). Furthermore, a representation, v, is called unitary if the matrix for v is unitary, or equivalently, if
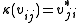 for all i, j.
for all i, j.
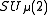
, where the parameter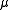 is a positive real number. So
is a positive real number. So 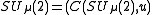 , where
, where 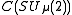 is the C*-algebra generated by
is the C*-algebra generated by  and
and  ,subject to
,subject to
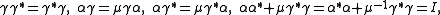
and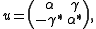 so that the comultiplication is determined by
so that the comultiplication is determined by 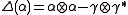 ,
,  , and the coinverse is determined by
, and the coinverse is determined by 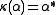 ,
, 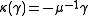 ,
, 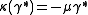 ,
, 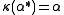 . Note that
. Note that  is a representation, but not a unitary representation
is a representation, but not a unitary representation
. is equivalent to the unitary representation
is equivalent to the unitary representation 
Equivalently,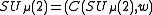 , where
, where 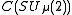 is the C*-algebra generated by
is the C*-algebra generated by  and
and 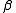 ,subject to
,subject to
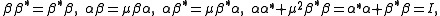
and so that the comultiplication is determined by
so that the comultiplication is determined by 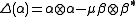 ,
, 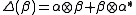 , and the coinverse is determined by
, and the coinverse is determined by  ,
,  ,
, 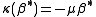 ,
, 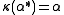 . Note that
. Note that 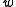 is a unitary representation. The realizations can be identified by equating
is a unitary representation. The realizations can be identified by equating 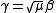 .
.
When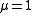 , then
, then 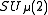 is equal to the concrete compact group
is equal to the concrete compact group 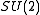 .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a compact quantum group is an abstract structure on a unital separable C*-algebra axiomatized from those that exist on the commutative C*-algebra of "continuous complex-valued functions" on a compact quantum group.
The basic motivation for this theory comes from the following analogy. The space of complex-valued functions on a compact Hausdorff topological space forms a commutative C*-algebra. On the other hand, by the Gelfand Theorem
Gelfand representation
In mathematics, the Gelfand representation in functional analysis has two related meanings:* a way of representing commutative Banach algebras as algebras of continuous functions;...
, a commutative C*-algebra is isomorphic to the C*-algebra of continuous complex-valued functions on a compact Hausdorff topological space, and the topological space is uniquely determined by the C*-algebra up to homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
.
S. L. Woronowicz
S. L. Woronowicz
Stanisław Lech Woronowicz is a Polish mathematician and physicist.It was Woronowicz, and Erling Størmer, who classified positive maps in the low dimensional cases. This translates to the Peres-Horodecki criterion, in the context of quantum information theory. He is also known for contributions to...
introduced the important concept of compact matrix quantum groups, which he initially called compact pseudogroups. Compact matrix quantum groups are abstract structures on which the "continuous functions" on the structure are given by elements of a C*-algebra. The geometry of a compact matrix quantum group is a special case of a noncommutative geometry
Noncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
.
Formulation
For a compact topological groupTopological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
,
 , there exists a C*-algebra homomorphism
, there exists a C*-algebra homomorphism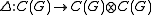
where
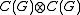 is the minimal C*-algebra tensor product — the completion of the algebraic tensor product
is the minimal C*-algebra tensor product — the completion of the algebraic tensor productTensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of
 and
and 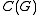 ) — such that
) — such that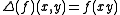
for all
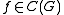 , and for all
, and for all 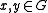 , where
, where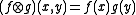
for all
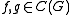 and all
and all 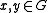 . There also exists a linear multiplicative mapping
. There also exists a linear multiplicative mapping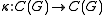 ,
,such that

for all
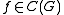 and all
and all 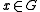 . Strictly speaking, this does not make
. Strictly speaking, this does not make 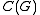 into a Hopf algebra
into a Hopf algebraHopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
, unless
 is finite.
is finite.On the other hand, a finite-dimensional representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of G can be used to generate a *-subalgebra of
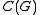 which is also a Hopf *-algebra. Specifically, if
which is also a Hopf *-algebra. Specifically, if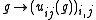
is an
 -dimensional representation
-dimensional representationRepresentation
Representation can refer to:* Representation , one's ability to influence the political process* Representative democracy* Representation, a type of diplomatic mission...
of
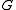 , then
, then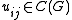
for all
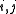 , and
, and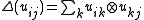
for all
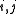 . It follows that the *-algebra generated by
. It follows that the *-algebra generated by 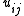 for all
for all 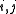 and
and 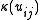 for all
for all 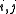 is a Hopf *-algebra: the counit is determined by
is a Hopf *-algebra: the counit is determined by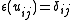
for all
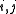 (where
(where 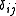 is the Kronecker delta), the antipode is
is the Kronecker delta), the antipode is  , and the unit is given by
, and the unit is given by
Compact Matrix Quantum Groups
As a generalization, a compact matrix quantum group is defined as a pair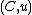 , where
, where 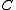 is a C*-algebra and
is a C*-algebra and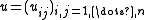
is a matrix with entries in
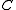 such that
such that- The *-subalgebra,
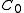 , of
, of 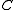 , which is generated by the matrix elements of
, which is generated by the matrix elements of  , is dense in
, is dense in  ;
;
- There exists a C*-algebra homomorphism
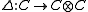 (where
(where  is the C*-algebra tensor product - the completion of the algebraic tensor product of
is the C*-algebra tensor product - the completion of the algebraic tensor product of 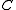 and
and 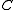 ) such that
) such that 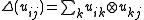 for all
for all 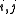 (
( is called the comultiplication);
is called the comultiplication);
- There exists a linear antimultiplicative map
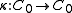 (the coinverse) such that
(the coinverse) such that 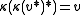 for all
for all 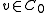 and
and 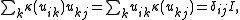 where
where 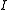 is the identity element of
is the identity element of 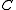 . Since
. Since  is antimultiplicative, then
is antimultiplicative, then 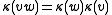 for all
for all 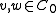 .
.
As a consequence of continuity, the comultiplication on
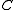 is coassociative.
is coassociative.In general,
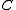 is a bialgebra, and
is a bialgebra, and 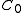 is a Hopf *-algebra.
is a Hopf *-algebra.Informally,
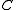 can be regarded as the *-algebra of continuous complex-valued functions over the compact matrix quantum group, and
can be regarded as the *-algebra of continuous complex-valued functions over the compact matrix quantum group, and  can be regarded as a finite-dimensional representation of the compact matrix quantum group.
can be regarded as a finite-dimensional representation of the compact matrix quantum group.Compact Quantum Groups
For C*-algebras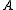 and
and 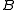 acting on the Hilbert spaces
acting on the Hilbert spaces 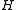 and
and 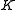 respectively, their minimal tensor product is defined to be the norm completion of the algebraic tensor product
respectively, their minimal tensor product is defined to be the norm completion of the algebraic tensor product 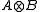 in
in 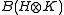 ; the norm completion is also denoted by
; the norm completion is also denoted by 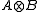 .
.A compact quantum group is defined as a pair
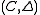 , where
, where 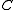 is a unital separable C*-algebra and
is a unital separable C*-algebra and
-
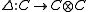 is a C*-algebra unital homomorphism satisfying
is a C*-algebra unital homomorphism satisfying  ; such that
; such that
- the sets
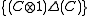 and
and 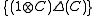 are dense in
are dense in 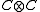 .
.
Representations
A representation of the compact matrix quantum group is given by a corepresentationCoalgebra
In mathematics, coalgebras or cogebras are structures that are dual to unital associative algebras. The axioms of unital associative algebras can be formulated in terms of commutative diagrams...
of the Hopf *-algebra (a corepresentation of a counital coassiative coalgebra
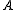 is a square matrix
is a square matrix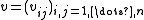
with entries in
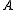 (so
(so  ) such that
) such that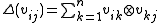
for all
 and
and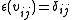 for all
for all  ). Furthermore, a representation, v, is called unitary if the matrix for v is unitary, or equivalently, if
). Furthermore, a representation, v, is called unitary if the matrix for v is unitary, or equivalently, if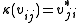 for all i, j.
for all i, j.Example
An example of a compact matrix quantum group is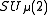
, where the parameter
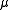 is a positive real number. So
is a positive real number. So 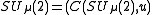 , where
, where 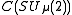 is the C*-algebra generated by
is the C*-algebra generated by  and
and  ,subject to
,subject to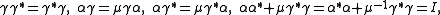
and
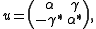 so that the comultiplication is determined by
so that the comultiplication is determined by 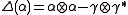 ,
,  , and the coinverse is determined by
, and the coinverse is determined by 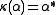 ,
, 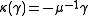 ,
, 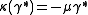 ,
, 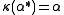 . Note that
. Note that  is a representation, but not a unitary representation
is a representation, but not a unitary representationUnitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
.
 is equivalent to the unitary representation
is equivalent to the unitary representation 
Equivalently,
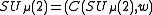 , where
, where 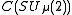 is the C*-algebra generated by
is the C*-algebra generated by  and
and 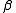 ,subject to
,subject to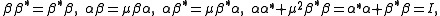
and
 so that the comultiplication is determined by
so that the comultiplication is determined by 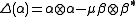 ,
, 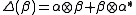 , and the coinverse is determined by
, and the coinverse is determined by  ,
,  ,
, 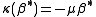 ,
, 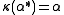 . Note that
. Note that 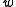 is a unitary representation. The realizations can be identified by equating
is a unitary representation. The realizations can be identified by equating 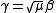 .
.When
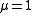 , then
, then 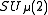 is equal to the concrete compact group
is equal to the concrete compact group 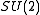 .
.

