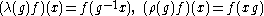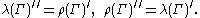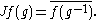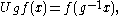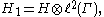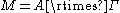Commutation theorem
Encyclopedia
In mathematics
, a commutation theorem explicitly identifies the commutant of a specific von Neumann algebra
acting on a Hilbert space
in the presence of a trace. The first such result was proved by F.J. Murray and John von Neumann
in the 1930s and applies to the von Neumann algebra generated by a discrete group
or by the dynamical system
associated with a
measurable transformation
preserving a probability measure
. Another important application is in the theory of unitary representation
s of unimodular
locally compact group
s, where the theory has been applied to the regular representation
and other closely related representations. In particular this framework led to an abstract version of the Plancherel theorem
for unimodular locally compact groups due to Irving Segal
and Forrest Stinespring and an abstract Plancherel theorem for spherical functions
associated with a Gelfand pair
due to Roger Godement
. Their work was put in final form in the 1950s by Jacques Dixmier
as part of the theory of Hilbert algebras. It was not until the late 1960s, prompted partly by results in algebraic quantum field theory and quantum statistical mechanics
due to the school of Rudolf Haag
, that the more general non-tracial Tomita–Takesaki theory was developed, heralding a new era in the theory of von Neumann algebras.
and M a von Neumann algebra
on H with a unit vector Ω such that
The vector Ω is called a cyclic-separating trace vector. It is called a trace vector because the last condition means that the matrix coefficient
corresponding to Ω defines a tracial state
on M. It is called cyclic since Ω generates H as a topological M-module. It is called separating
because if aΩ = 0 for a in M, then aMΩ= (0), and hence a = 0.
It follows that the map
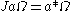
for a in M defines a conjugate-linear isometry of H with square the identity J2 = I. The operator J is usually called the modular conjugation operator.
It is immediately verified that JMJ and M commute on the subspace M Ω, so that
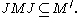
The commutation theorem of Murray and von Neumann states that
One of the easiest ways to see this is to introduce K, the closure of the real
subspace Msa Ω, where Msa denotes the self-adjoint elements in M. It follows that
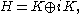
an orthogonal direct sum for the real part of inner product. This is just the real orthogonal decomposition for the ±1 eigenspaces of J.
On the other hand for a in Msa and b in Msa, the inner product (abΩ, Ω) is real, because ab is self-adjoint. Hence K is unaltered if M is replaced by M '.
In particular Ω is a trace vector for M and J is unaltered if M is replaced by M '. So the opposite inclusion
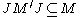
follows by reversing the roles of M and M.
One of the most important cases of the group–measure space construction is when Γ is the group of integers Z, i.e. the case of a single invertible
measurable transformation T. Here T must preserve the probability measure μ. Semifinite traces are required to handle the case when T (or more generally Γ) only preserves an infinite equivalent measure; and the full force of the Tomita–Takesaki theory is required when there is no invariant measure in the equivalence class, even though the equivalence class of the measure is preserved by T (or Γ).
If in addition τ is non-zero on every non-zero projection, then τ is called a faithful trace.
If τ is a faithul trace on M, let H = L2(M, τ) be the Hilbert space completion of the inner product space
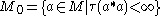
with respect to the inner product
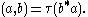
The von Neumann algebra M acts by left multiplication on H and can be identified with its image. Let
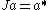
for a in M0. The operator J is again called the modular conjugation operator and extends to a conjugate-linear isometry of H satisfying J2 = I. The commutation theorem of Murray and von Neumann
is again valid in this case. This result can be proved directly by a variety of methods, but follows immediately from the result for finite traces, by repeated use of the following elementary fact:
naturally lead to examples of Hilbert algebras. Every von Neumann algebra endowed with a semifinite trace has a canonical "completed" or "full" Hilbert algebra associated with it; and conversely a completed Hilbert algebra of exactly this form can be canonically associated with every Hilbert algebra. The theory of Hilbert algebras can be used to deduce the commutation theorems of Murray and von Neumann; equally well the main results on Hilbert algebras can also be deduced directly from the commutation theorems for traces. The theory of Hilbert algebras was generalised by Takesaki as a tool for proving commutation theorems for semifinite weights in Tomita–Takesaki theory; they can be dispensed with when dealing with states.
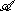 with involution x→x* and an inner product such that
with involution x→x* and an inner product such that
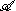 with respect to the inner product and let J denote the extension of the involution to a conjugate-linear involution of H. Define a representation λ and an anti-representation ρ of
with respect to the inner product and let J denote the extension of the involution to a conjugate-linear involution of H. Define a representation λ and an anti-representation ρ of
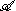 on itself by left and right multiplication:
on itself by left and right multiplication:
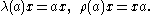
These actions extend continuously to actions on H. In this case the commutation theorem for Hilbert algebras
states that
Moreover if
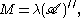
the von Neumann algebra generated by the operators λ(a), then
These results were proved independently by and .
The proof relies on the notion of "bounded elements" in the Hilbert space completion H.
An element of x in H is said to be bounded (relative to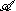 ) if the map a → xa of
) if the map a → xa of 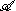 into H extends to a
into H extends to a
bounded operator on H, denoted by λ(x). In this case it is straightforward to prove that:
The commutation theorem follows immediately from the last assertion. In particular
The space of all bounded elements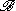 forms a Hilbert algebra containing
forms a Hilbert algebra containing 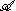 as a dense *-subalgebra. It is said to be completed or full because any element in H bounded relative to
as a dense *-subalgebra. It is said to be completed or full because any element in H bounded relative to 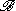 must actually already lie in
must actually already lie in 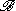 . The functional τ on M+ defined by
. The functional τ on M+ defined by
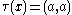
if x =λ(a)*λ(a) and ∞ otherwise, yields a faithful semifinite trace on M with
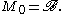
Thus:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a commutation theorem explicitly identifies the commutant of a specific von Neumann algebra
Von Neumann algebra
In mathematics, a von Neumann algebra or W*-algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. They were originally introduced by John von Neumann, motivated by his study of single operators, group...
acting on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
in the presence of a trace. The first such result was proved by F.J. Murray and John von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
in the 1930s and applies to the von Neumann algebra generated by a discrete group
Discrete group
In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
or by the dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
associated with a
measurable transformation
Ergodic theory
Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
preserving a probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
. Another important application is in the theory of unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
s of unimodular
Haar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
locally compact group
Locally compact group
In mathematics, a locally compact group is a topological group G which is locally compact as a topological space. Locally compact groups are important because they have a natural measure called the Haar measure. This allows one to define integrals of functions on G.Many of the results of finite...
s, where the theory has been applied to the regular representation
Regular representation
In mathematics, and in particular the theory of group representations, the regular representation of a group G is the linear representation afforded by the group action of G on itself by translation....
and other closely related representations. In particular this framework led to an abstract version of the Plancherel theorem
Plancherel theorem
In mathematics, the Plancherel theorem is a result in harmonic analysis, proved by Michel Plancherel in 1910. It states that the integral of a function's squared modulus is equal to the integral of the squared modulus of its frequency spectrum....
for unimodular locally compact groups due to Irving Segal
Irving Segal
Irving Ezra Segal was a mathematician known for work on theoretical quantum mechanics.He was at the Massachusetts Institute of Technology...
and Forrest Stinespring and an abstract Plancherel theorem for spherical functions
Plancherel theorem for spherical functions
In mathematics, the Plancherel theorem for spherical functions is an important result in the representation theory of semisimple Lie groups, due in its final form to Harish-Chandra...
associated with a Gelfand pair
Gelfand pair
In mathematics, the expression Gelfand pair is a pair consisting of a group G and a subgroup K that satisfies a certain property on restricted representations. The theory of Gelfand pairs is closely related to the topic of spherical functions in the classical theory of special functions, and to...
due to Roger Godement
Roger Godement
Roger Godement is a French mathematician, known for his work in functional analysis, and also his expository books.He started as a student at the École normale supérieure in 1940, where he became a student of Henri Cartan...
. Their work was put in final form in the 1950s by Jacques Dixmier
Jacques Dixmier
Jacques Dixmier is a French mathematician. He worked on operator algebras, and wrote several of the standard reference books on them, and introduced the Dixmier trace. He received his Ph.D. in 1949 from the University of Paris, and his students include Alain Connes.-Publications:*J. Dixmier,...
as part of the theory of Hilbert algebras. It was not until the late 1960s, prompted partly by results in algebraic quantum field theory and quantum statistical mechanics
Quantum statistical mechanics
Quantum statistical mechanics is the study of statistical ensembles of quantum mechanical systems. A statistical ensemble is described by a density operator S, which is a non-negative, self-adjoint, trace-class operator of trace 1 on the Hilbert space H describing the quantum system. This can be...
due to the school of Rudolf Haag
Rudolf Haag
Rudolf Haag is a German physicist. He is best known for his contributions to the algebraic formulation of axiomatic quantum field theory, namely the Haag-Kastler axioms...
, that the more general non-tracial Tomita–Takesaki theory was developed, heralding a new era in the theory of von Neumann algebras.
Commutation theorem for finite traces
Let H be a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
and M a von Neumann algebra
Von Neumann algebra
In mathematics, a von Neumann algebra or W*-algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. They were originally introduced by John von Neumann, motivated by his study of single operators, group...
on H with a unit vector Ω such that
- M Ω is dense in H
- M ' Ω is dense in H, where M ' denotes the commutant of M
- (abΩ, Ω) = (baΩ, Ω) for all a, b in M.
The vector Ω is called a cyclic-separating trace vector. It is called a trace vector because the last condition means that the matrix coefficient
Matrix coefficient
In mathematics, a matrix coefficient is a function on agroup of a special form, which depends on a linear representation of the group and additional data...
corresponding to Ω defines a tracial state
State (functional analysis)
In functional analysis, a state on a C*-algebra is a positive linear functional of norm 1. The set of states of a C*-algebra A, sometimes denoted by S, is always a convex set. The extremal points of S are called pure states...
on M. It is called cyclic since Ω generates H as a topological M-module. It is called separating
because if aΩ = 0 for a in M, then aMΩ= (0), and hence a = 0.
It follows that the map
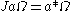
for a in M defines a conjugate-linear isometry of H with square the identity J2 = I. The operator J is usually called the modular conjugation operator.
It is immediately verified that JMJ and M commute on the subspace M Ω, so that
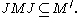
The commutation theorem of Murray and von Neumann states that
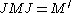 |
One of the easiest ways to see this is to introduce K, the closure of the real
subspace Msa Ω, where Msa denotes the self-adjoint elements in M. It follows that
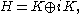
an orthogonal direct sum for the real part of inner product. This is just the real orthogonal decomposition for the ±1 eigenspaces of J.
On the other hand for a in Msa and b in Msa, the inner product (abΩ, Ω) is real, because ab is self-adjoint. Hence K is unaltered if M is replaced by M '.
In particular Ω is a trace vector for M and J is unaltered if M is replaced by M '. So the opposite inclusion
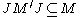
follows by reversing the roles of M and M.
Examples
- One of the simplest cases of the commutation theorem, where it can easily be seen directly, is that of a finite groupFinite groupIn mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
Γ acting on the finite-dimensional inner product spaceInner product spaceIn mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
 by the left and right regular representationRegular representationIn mathematics, and in particular the theory of group representations, the regular representation of a group G is the linear representation afforded by the group action of G on itself by translation....
by the left and right regular representationRegular representationIn mathematics, and in particular the theory of group representations, the regular representation of a group G is the linear representation afforded by the group action of G on itself by translation....
s λ and ρ. These unitary representationUnitary representationIn mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
s are given by the formulas
- for f in
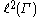 and the commutation theorem implies that
and the commutation theorem implies that
- The operator J is given by the formula
- Exactly the same results remain true if Γ is allowed to be any countable discrete groupDiscrete groupIn mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
. The von Neumann algebra λ(Γ)' ' is usually called the group von Neumann algebra of Γ.
- Another important example is provided by a probability spaceProbability spaceIn probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
(X, μ). The Abelian von Neumann algebraAbelian von Neumann algebraIn functional analysis, an abelian von Neumann algebra is a von Neumann algebra of operators on a Hilbert space in which all elements commute.The prototypical example of an abelian von Neumann algebra is...
A = L∞(X, μ) acts by multiplication operatorMultiplication operatorIn operator theory, a multiplication operator is a linear operator T defined on some vector space of functions and whose value at a function φ is given by multiplication by a fixed function f...
s on H = L2(X, μ) and the constant function 1 is a cyclic-separating trace vector. It follows that
- so that A is a maximal Abelian subalgebra of B(H), the von Neumann algebra of all bounded operatorBounded operatorIn functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
s on H.
- The third class of examples combines the above two. Coming from ergodic theoryErgodic theoryErgodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
, it was one of von Neumann's original motivations for studying von Neumann algebras. Let (X, μ) be a probability space and let Γ be a countable discrete group of measure-preserving transformations of (X, μ). The group therefore acts unitarily on the Hilbert space H = L2(X, μ) according to the formula
- for f in H and normalises the Abelian von Neumann algebra A = L∞(X, μ). Let
- a tensor productTensor productIn mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of Hilbert spaces. The group–measure space construction or crossed productCrossed productIn mathematics, and more specifically in the theory of von Neumann algebras, a crossed productis a basic method of constructing a new von Neumann algebra froma von Neumann algebra acted on by a group. It is related to...
von Neumann algebra
- is defined to be the von Neumann algebra on H1 generated by the algebra
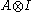 and the normalising operators
and the normalising operators 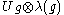 .
.
- The vector
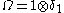 is a cyclic-separating trace vector. Moreover the modular conjugation operator J and commutant M ' can be explicitly identified.
is a cyclic-separating trace vector. Moreover the modular conjugation operator J and commutant M ' can be explicitly identified.
One of the most important cases of the group–measure space construction is when Γ is the group of integers Z, i.e. the case of a single invertible
measurable transformation T. Here T must preserve the probability measure μ. Semifinite traces are required to handle the case when T (or more generally Γ) only preserves an infinite equivalent measure; and the full force of the Tomita–Takesaki theory is required when there is no invariant measure in the equivalence class, even though the equivalence class of the measure is preserved by T (or Γ).
Commutation theorem for semifinite traces
Let M be a von Neumann algebra and M+ the set of positive operators in M. By definition, a semifinite trace (or sometimes just trace) on M is a functional τ from M+ into [0,∞] such that-
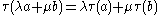 for a, b in M+ and λ, μ ≥ 0 ();
for a, b in M+ and λ, μ ≥ 0 (); -
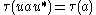 for a in M+ and u a unitary operatorUnitary operatorIn functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
for a in M+ and u a unitary operatorUnitary operatorIn functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
in M (unitary invariance); - τ is completely additive on orthogonal families of projections in M (normality);
- each projection in M is as orthogonal direct sum of projections with finite trace (semifiniteness).
If in addition τ is non-zero on every non-zero projection, then τ is called a faithful trace.
If τ is a faithul trace on M, let H = L2(M, τ) be the Hilbert space completion of the inner product space
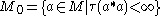
with respect to the inner product
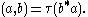
The von Neumann algebra M acts by left multiplication on H and can be identified with its image. Let
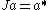
for a in M0. The operator J is again called the modular conjugation operator and extends to a conjugate-linear isometry of H satisfying J2 = I. The commutation theorem of Murray and von Neumann
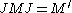 |
is again valid in this case. This result can be proved directly by a variety of methods, but follows immediately from the result for finite traces, by repeated use of the following elementary fact:
- If M1
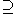 M2 are two von Neumann algebras such that pn M1 = pn M2 for a family of projections pn in the commutant of M1 increasing to I in the strong operator topologyStrong operator topologyIn functional analysis, a branch of mathematics, the strong operator topology, often abbreviated SOT, is the weakest locally convex topology on the set of bounded operators on a Hilbert space such that the evaluation map sending an operator T to the real number \|Tx\| is continuous for each vector...
M2 are two von Neumann algebras such that pn M1 = pn M2 for a family of projections pn in the commutant of M1 increasing to I in the strong operator topologyStrong operator topologyIn functional analysis, a branch of mathematics, the strong operator topology, often abbreviated SOT, is the weakest locally convex topology on the set of bounded operators on a Hilbert space such that the evaluation map sending an operator T to the real number \|Tx\| is continuous for each vector...
, then M1 = M2.
Hilbert algebras
The theory of Hilbert algebras was introduced by Godement (under the name "unitary algebras"), Segal and Dixmier to formalize the classical method of defining the trace for trace class operators starting from Hilbert-Schmidt operators. Applications in the representation theory of groupsUnitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
naturally lead to examples of Hilbert algebras. Every von Neumann algebra endowed with a semifinite trace has a canonical "completed" or "full" Hilbert algebra associated with it; and conversely a completed Hilbert algebra of exactly this form can be canonically associated with every Hilbert algebra. The theory of Hilbert algebras can be used to deduce the commutation theorems of Murray and von Neumann; equally well the main results on Hilbert algebras can also be deduced directly from the commutation theorems for traces. The theory of Hilbert algebras was generalised by Takesaki as a tool for proving commutation theorems for semifinite weights in Tomita–Takesaki theory; they can be dispensed with when dealing with states.
Definition
A Hilbert algebra is an algebra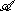 with involution x→x* and an inner product such that
with involution x→x* and an inner product such that- (a,b)=(b*,a*) for a, b in
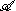 ;
; - left multiplication by a fixed a in
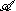 is a bounded operator;
is a bounded operator; - * is the adjoint, in other words (xy,z) = (y, x*z);
- the linear span of all products xy is dense in
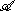 .
.
Examples
- The Hilbert-Schmidt operators on an infinite-dimensional Hilbert space form a Hilbert algebra with inner product (a,b) = Tr (b*a).
- If (X, μ) is an infinite measure space, the algebra L∞ (X)
 L2(X) is a Hilbert algebra with the usual inner product from L2(X).
L2(X) is a Hilbert algebra with the usual inner product from L2(X). - If M is a von Neumann algebra with faithful semifinite trace τ, then the *-subalgebra M0 defined above is a Hilbert algebra with inner product (a, b) = τ(b*a).
- If G is a unimodularHaar measureIn mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
locally compact groupLocally compact groupIn mathematics, a locally compact group is a topological group G which is locally compact as a topological space. Locally compact groups are important because they have a natural measure called the Haar measure. This allows one to define integrals of functions on G.Many of the results of finite...
, the convolution algebra L1(G) L2(G) is a Hilbert algebra with the usual inner product from L2(G).
L2(G) is a Hilbert algebra with the usual inner product from L2(G). - If (G, K) is a Gelfand pairGelfand pairIn mathematics, the expression Gelfand pair is a pair consisting of a group G and a subgroup K that satisfies a certain property on restricted representations. The theory of Gelfand pairs is closely related to the topic of spherical functions in the classical theory of special functions, and to...
, the convolution algebra L1(K\G/K) L2(K\G/K) is a Hilbert algebra with the usual inner product from L2(G); here Lp(K\G/K) denotes the closed subspace of K-biinvariant functions in Lp(G).
L2(K\G/K) is a Hilbert algebra with the usual inner product from L2(G); here Lp(K\G/K) denotes the closed subspace of K-biinvariant functions in Lp(G). - Any dense *-subalgebra of a Hilbert algebra is also a Hilbert algebra.
Properties
Let H be the Hilbert space completion of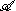 with respect to the inner product and let J denote the extension of the involution to a conjugate-linear involution of H. Define a representation λ and an anti-representation ρ of
with respect to the inner product and let J denote the extension of the involution to a conjugate-linear involution of H. Define a representation λ and an anti-representation ρ of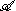 on itself by left and right multiplication:
on itself by left and right multiplication: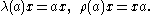
These actions extend continuously to actions on H. In this case the commutation theorem for Hilbert algebras
states that
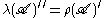 |
Moreover if
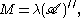
the von Neumann algebra generated by the operators λ(a), then
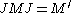 |
These results were proved independently by and .
The proof relies on the notion of "bounded elements" in the Hilbert space completion H.
An element of x in H is said to be bounded (relative to
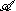 ) if the map a → xa of
) if the map a → xa of 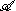 into H extends to a
into H extends to abounded operator on H, denoted by λ(x). In this case it is straightforward to prove that:
- Jx is also a bounded element, denoted x*, and λ(x*) = λ(x)*;
- a → ax is given by the bounded operator ρ(x) = Jλ(x*)J on H;
- M ' is generated by the ρ(x)'s with x bounded;
- λ(x) and ρ(y) commute for x, y bounded.
The commutation theorem follows immediately from the last assertion. In particular
- M = λ(
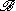 )".
)".
The space of all bounded elements
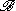 forms a Hilbert algebra containing
forms a Hilbert algebra containing 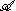 as a dense *-subalgebra. It is said to be completed or full because any element in H bounded relative to
as a dense *-subalgebra. It is said to be completed or full because any element in H bounded relative to 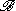 must actually already lie in
must actually already lie in 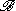 . The functional τ on M+ defined by
. The functional τ on M+ defined by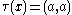
if x =λ(a)*λ(a) and ∞ otherwise, yields a faithful semifinite trace on M with
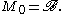
Thus:
| There is a one-one correspondence between von Neumann algebras on H with faithful semifinite trace and full Hilbert algebras with Hilbert space completion H. |