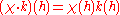Crossed product
Encyclopedia
In mathematics
, and more specifically in the theory of von Neumann algebra
s, a crossed product
is a basic method of constructing a new von Neumann algebra from
a von Neumann algebra acted on
by a group
. It is related to
the semidirect product
construction for groups. (Roughly speaking, crossed product is the expected structure for a group ring
of a semidirect product group. Therefore crossed products have a ring theory
aspect also. This article concentrates on an important case, where they appear in functional analysis
.)
s G and N with an action of G on N we can form the semidirect product
. This contains N
as a normal subgroup
, and the action of G on N is given by conjugation
in the semidirect product. We can replace N by its complex group algebra
C[N], and again form a product
in a similar way; this algebra is a sum of subspaces
gC[N] as g runs through the elements of G, and is the group algebra of
.
We can generalize this construction further by replacing C[N]
by any algebra A acted on by G to get a crossed product
, which is the sum of subspaces
gA and where the action of G on A is given by conjugation in the crossed product.
The crossed product of a von Neumann algebra by a group G acting on it is similar except that we have to be more careful about topologies
, and need to construct a Hilbert space
acted on by the crossed product. (Note that the von Neumann algebra crossed product is usually larger than the algebraic crossed product discussed above; in fact it is some sort of completion of the algebraic crossed product.)
of operators acting on a Hilbert space H and G is a discrete group acting on A. We let K be the Hilbert space of all square summable H-valued functions on G. There is an action of A on K
given by
for k in K, g, h in G, and a in A,
and there is an action of G on K given by
The crossed product
is the von Neumann algebra acting on K generated by the actions of A and G on K. It does not depend (up to isomorphism) on the choice of the Hilbert space H.
This construction can be extended to work for any locally compact group G acting on any von Neumann algebra A. When
is an abelian von Neumann algebra
, this is the original group-measure space construction of Murray and von Neumann.
A has no non-zero projections p such that some nontrivial g fixes
all elements of pAp. The action is called ergodic if
the only invariant projections are 0 and 1.
Usually A can be identified as the abelian von Neumann algebra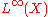
of essentially bounded functions on a measure space X acted on by G, and then the action of G on X is ergodic (for any measurable invariant subset, either the subset or its complement has measure 0) if and only if the action of G on A is ergodic.
If the action of G on A is free and ergodic
then the crossed product
is a factor.
Moreover:
In particular one can construct examples of all the different types of factors as crossed products.
is a von Neumann algebra
on which a locally compact Abelian
acts, then 
, the dual group
of characters
of 
, acts by unitaries on 
:
These unitaries normalise the crossed product, defining the dual action of
. Together with the crossed product, they generate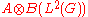 
, which
can be identified with the iterated crossed product by the dual action
. Under this identification, the double dual action of 
(the dual group of 
) corresponds to the tensor product of the original action on 
and conjugation by the following unitaries on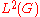 
:
The crossed product may be identified with the fixed point algebra of the double dual action. More generally
is the fixed point algebra of 
in the crossed product.
Similar statements hold when
is replaced by a non-Abelian locally compact group or more generally a locally compact quantum group
, a class of Hopf algebra
related to von Neumann algebra
s. An analogous theory has also been developed for actions on C* algebras and their crossed products.
Duality first appeared for actions of the reals
in the work of Connes
and Takesaki on the classification of Type III factors.
According to Tomita–Takesaki theory, every vector which is cyclic for the factor and its commutant gives rise to a 1-parameter modular automorphism group. The corresponding crossed product is a Type
von Neumann algebra
and the corresponding dual action restricts to an ergodic action of the reals
on its centre, an Abelian von Neumann algebra
. This ergodic flow is called the flow of weights; it is independent of the choice of cyclic vector. The Connes spectrum, a closed subgroup of the positive reals
, is obtained by applying the exponential to the kernel of this flow.
Connes
and Haagerup proved that the Connes spectrum and the flow of weights are complete invariants of hyperfinite
Type III factors.
From this classification and results in ergodic theory
, it is known that every infinite-dimensional hyperfinite factor has the form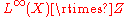
for some free ergodic action of 
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and more specifically in the theory of von Neumann algebra
Von Neumann algebra
In mathematics, a von Neumann algebra or W*-algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. They were originally introduced by John von Neumann, motivated by his study of single operators, group...
s, a crossed product
is a basic method of constructing a new von Neumann algebra from
a von Neumann algebra acted on
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
by a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. It is related to
the semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
construction for groups. (Roughly speaking, crossed product is the expected structure for a group ring
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
of a semidirect product group. Therefore crossed products have a ring theory
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
aspect also. This article concentrates on an important case, where they appear in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
.)
Motivation
Recall that if we have two finite groupFinite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s G and N with an action of G on N we can form the semidirect product
. This contains Nas a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
, and the action of G on N is given by conjugation
Inner automorphism
In abstract algebra an inner automorphism is a functionwhich, informally, involves a certain operation being applied, then another one performed, and then the initial operation being reversed...
in the semidirect product. We can replace N by its complex group algebra
Group algebra
In mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
C[N], and again form a product
in a similar way; this algebra is a sum of subspacesDirect sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
gC[N] as g runs through the elements of G, and is the group algebra of
.We can generalize this construction further by replacing C[N]
by any algebra A acted on by G to get a crossed product
, which is the sum of subspacesgA and where the action of G on A is given by conjugation in the crossed product.
The crossed product of a von Neumann algebra by a group G acting on it is similar except that we have to be more careful about topologies
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, and need to construct a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
acted on by the crossed product. (Note that the von Neumann algebra crossed product is usually larger than the algebraic crossed product discussed above; in fact it is some sort of completion of the algebraic crossed product.)
Construction
Suppose that A is a von Neumann algebraVon Neumann algebra
In mathematics, a von Neumann algebra or W*-algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. They were originally introduced by John von Neumann, motivated by his study of single operators, group...
of operators acting on a Hilbert space H and G is a discrete group acting on A. We let K be the Hilbert space of all square summable H-valued functions on G. There is an action of A on K
given by
- a(k)(g) = g-1(a)k(g)
for k in K, g, h in G, and a in A,
and there is an action of G on K given by
- g(k)(h) = k(g-1h).
The crossed product
is the von Neumann algebra acting on K generated by the actions of A and G on K. It does not depend (up to isomorphism) on the choice of the Hilbert space H.This construction can be extended to work for any locally compact group G acting on any von Neumann algebra A. When
is an abelian von Neumann algebraAbelian von Neumann algebra
In functional analysis, an abelian von Neumann algebra is a von Neumann algebra of operators on a Hilbert space in which all elements commute.The prototypical example of an abelian von Neumann algebra is...
, this is the original group-measure space construction of Murray and von Neumann.
Properties
We let G be an infinite countable discrete group acting on the abelian von Neumann algebra A. The action is called free ifA has no non-zero projections p such that some nontrivial g fixes
all elements of pAp. The action is called ergodic if
the only invariant projections are 0 and 1.
Usually A can be identified as the abelian von Neumann algebra
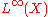of essentially bounded functions on a measure space X acted on by G, and then the action of G on X is ergodic (for any measurable invariant subset, either the subset or its complement has measure 0) if and only if the action of G on A is ergodic.If the action of G on A is free and ergodic
then the crossed product
is a factor.Moreover:
- The factor is of type I if A has a minimal projection such that 1 is the sum of the G conjugates of this projection. This corresponds to the action of G on X being transitive. Example: X is the integers, and G is the group of integers acting by translations.
- The factor has type II1 if A has a faithful finite normal G-invariant trace. This corresponds to X having a finite G invariant measure, absolutely continuous with respect to the measure on X. Example: X is the unit circle in the complex plane, and G is the group of all roots of unity.
- The factor has type II∞ if it is not of types I or II1 and has a faithful semifinite normal G-invariant trace. This corresponds to X having an infinite G invariant measure without atoms, absolutely continuous with respect to the measure on X. Example: X is the real line, and G is the group of rationals acting by translations.
- The factor has type III if A has no faithful semifinite normal G-invariant trace. This corresponds to X having no non-zero absolutely continuous G-invariant measure. Example: X is the real line, and G is the group of all transformations ax+b for a and b rational, a non-zero.
In particular one can construct examples of all the different types of factors as crossed products.
Duality
If is a von Neumann algebraVon Neumann algebra
In mathematics, a von Neumann algebra or W*-algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. They were originally introduced by John von Neumann, motivated by his study of single operators, group...
on which a locally compact Abelian
acts, then , the dual groupDual group
In mathematics, the dual group may be:* The Pontryagin dual of a locally compact abelian group* The Langlands dual of a reductive algebraic group* The Deligne-Lusztig dual of a reductive group over a finite field....
of characters
Character (mathematics)
In mathematics, a character is a special kind of function from a group to a field . There are at least two distinct, but overlapping meanings...
of , acts by unitaries on :
These unitaries normalise the crossed product, defining the dual action of
. Together with the crossed product, they generate 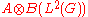, whichcan be identified with the iterated crossed product by the dual action
. Under this identification, the double dual action of (the dual group of ) corresponds to the tensor product of the original action on and conjugation by the following unitaries on :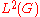
The crossed product may be identified with the fixed point algebra of the double dual action. More generally
is the fixed point algebra of in the crossed product.Similar statements hold when
is replaced by a non-Abelian locally compact group or more generally a locally compact quantum groupLocally compact quantum group
The locally compact quantum group is a relatively new C*-algebraic formalism for quantum groups, generalizing the Kac algebra, compact quantum group and Hopf algebra approaches. Earlier attempts of a unifying definition of quantum groups using e.g...
, a class of Hopf algebra
Hopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
related to von Neumann algebra
Von Neumann algebra
In mathematics, a von Neumann algebra or W*-algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. They were originally introduced by John von Neumann, motivated by his study of single operators, group...
s. An analogous theory has also been developed for actions on C* algebras and their crossed products.
Duality first appeared for actions of the reals
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
in the work of Connes
Alain Connes
Alain Connes is a French mathematician, currently Professor at the Collège de France, IHÉS, The Ohio State University and Vanderbilt University.-Work:...
and Takesaki on the classification of Type III factors.
According to Tomita–Takesaki theory, every vector which is cyclic for the factor and its commutant gives rise to a 1-parameter modular automorphism group. The corresponding crossed product is a Type
von Neumann algebraVon Neumann algebra
In mathematics, a von Neumann algebra or W*-algebra is a *-algebra of bounded operators on a Hilbert space that is closed in the weak operator topology and contains the identity operator. They were originally introduced by John von Neumann, motivated by his study of single operators, group...
and the corresponding dual action restricts to an ergodic action of the reals
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
on its centre, an Abelian von Neumann algebra
Abelian von Neumann algebra
In functional analysis, an abelian von Neumann algebra is a von Neumann algebra of operators on a Hilbert space in which all elements commute.The prototypical example of an abelian von Neumann algebra is...
. This ergodic flow is called the flow of weights; it is independent of the choice of cyclic vector. The Connes spectrum, a closed subgroup of the positive reals
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, is obtained by applying the exponential to the kernel of this flow.
- When the kernel is the whole of
, the factor is type 
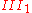. - When the kernel is
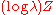for 
in (0,1), the factor is type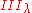 
. - When the kernel is trivial, the factor is type
.
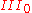Connes
Alain Connes
Alain Connes is a French mathematician, currently Professor at the Collège de France, IHÉS, The Ohio State University and Vanderbilt University.-Work:...
and Haagerup proved that the Connes spectrum and the flow of weights are complete invariants of hyperfinite
Hyperfinite
Hyperfinite may refer to:*Hyperfinite set*von Neumann algebra...
Type III factors.
From this classification and results in ergodic theory
Ergodic theory
Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
, it is known that every infinite-dimensional hyperfinite factor has the form
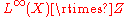for some free ergodic action of .Examples
- If we take the algebra A to be the complex numbers C, then the crossed product
is called the von Neumann group algebra of G.
- If G is an infinite discrete group such that every conjugacy class has infinite order then the von Neumann group algebra is a factor of type II1. Moreover if every finite set of elements of G generates a finite subgroup (or more generally if G is amenable) then the factor is the hyperfinite factor of type II1.