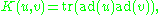Cartan's criterion
Encyclopedia
In mathematics, Cartan's criterion gives conditions for a Lie algebra
in characteristic 0 to be solvable, which implies a related criterion for the Lie algebra to be semisimple. It is based on the notion of the Killing form
, a symmetric bilinear form
on defined by the formula
defined by the formula
where tr denotes the trace of a linear operator
. The criterion was introduced by .
The fact that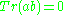 in the solvable case follows immediately from Lie's theorem
in the solvable case follows immediately from Lie's theorem
that solvable Lie algebras in characteristic 0 can be put in upper triangular form.
Applying Cartan's criterion to the adjoint representation gives:
gave a very short proof that if a finite dimensional Lie algebra (in any characteristic) has a non-degenerate invariant bilinear form
and no non-zero abelian ideals, and in particular if its Killing form is non-degenerate, then it is a sum of simple Lie algebras.
Conversely, it follows easily from Cartan's criterion for solvability that a semisimple algebra (in characteristic 0) has a non-degenerate Killing form.
If a finite dimensional Lie algebra is nilpotent, then the Killing form is identically zero (and more generally the Killing form vanishes on any nilpotent ideal). The converse is false: there are non-nilpotent Lie algebras whose Killing form vanishes. An example is given by the semidirect product of an abelian Lie algebra V with a 1-dimensional Lie algebra acting on V as an endomorphism b such that b is not nilpotent and Tr(b2)=0.
In characteristic 0, every reductive Lie algebra (one that is a sum of abelian and simple Lie algebras) has a non-degenerate invariant symmetric bilinear form. However the converse is false: a Lie algebra with a non-degenerate invariant symmetric bilinear form need not be a sum of simple and abelian Lie algebras. A typical counterexample is G = L[t]/tnL[t] where n>1, L is a simple complex Lie algebra with a bilinear form , and the bilinear form on G is given by taking the coefficient of tn−1 of the C[t]-valued bilinear form on G induced by the form on L. The bilinear form is non-degenerate, but the Lie algebra is not a sum of simple and abelian Lie algebras.
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
in characteristic 0 to be solvable, which implies a related criterion for the Lie algebra to be semisimple. It is based on the notion of the Killing form
Killing form
In mathematics, the Killing form, named after Wilhelm Killing, is a symmetric bilinear form that plays a basic role in the theories of Lie groups and Lie algebras...
, a symmetric bilinear form
Symmetric bilinear form
A symmetric bilinear form is a bilinear form on a vector space that is symmetric. Symmetric bilinear forms are of great importance in the study of orthogonal polarity and quadrics....
on
 defined by the formula
defined by the formula
where tr denotes the trace of a linear operator
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
. The criterion was introduced by .
Cartan's criterion for solvability
Cartan's criterion for solvability states:- A Lie subalgebra
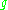 of endomorphisms of a finite dimensional vector space over a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of endomorphisms of a finite dimensional vector space over a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of characteristic zero is solvable if and only if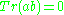 whenever
whenever 
The fact that
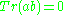 in the solvable case follows immediately from Lie's theorem
in the solvable case follows immediately from Lie's theoremLie–Kolchin theorem
In mathematics, the Lie–Kolchin theorem is a theorem in the representation theory of linear algebraic groups; Lie's theorem is the analog for linear Lie algebras....
that solvable Lie algebras in characteristic 0 can be put in upper triangular form.
Applying Cartan's criterion to the adjoint representation gives:
- A finite-dimensional Lie algebra
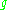 over a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
over a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of characteristic zero is solvable if and only if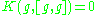 (where K is the Killing form).
(where K is the Killing form).
Cartan's criterion for semisimplicity
Cartan's criterion for semisimplicity states:- A finite-dimensional Lie algebra
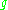 over a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
over a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of characteristic zero is semisimple if and only if the Killing form is non-degenerateDegenerate formIn mathematics, specifically linear algebra, a degenerate bilinear form ƒ on a vector space V is one such that the map from V to V^* given by v \mapsto is not an isomorphism...
.
gave a very short proof that if a finite dimensional Lie algebra (in any characteristic) has a non-degenerate invariant bilinear form
Quadratic Lie algebra
A quadratic Lie algebra is a Lie algebra together with a compatible symmetric bilinear form. Compatibility means that it is invariant under the adjoint representation...
and no non-zero abelian ideals, and in particular if its Killing form is non-degenerate, then it is a sum of simple Lie algebras.
Conversely, it follows easily from Cartan's criterion for solvability that a semisimple algebra (in characteristic 0) has a non-degenerate Killing form.
Examples
Cartan's criteria fail in characteristic p>0; for example:- the Lie algebra SLp(k) is simple if k has characteristic not 2 and has vanishing Killing form, though it does have an nonzero invariant bilinear form given by (a,b) = Tr(ab).
- the Lie algebra with basis an for n∈Z/pZ and bracket [ai,aj] = (i−j)ai+j is simple for p>2 but has no nonzero invariant bilinear form.
- If k has characteristic 2 then the semidirect product gl2(k).k2 is a solvable Lie algebra, but the Killing form is not identically zero on its derived algebra sl2(k).k2.
If a finite dimensional Lie algebra is nilpotent, then the Killing form is identically zero (and more generally the Killing form vanishes on any nilpotent ideal). The converse is false: there are non-nilpotent Lie algebras whose Killing form vanishes. An example is given by the semidirect product of an abelian Lie algebra V with a 1-dimensional Lie algebra acting on V as an endomorphism b such that b is not nilpotent and Tr(b2)=0.
In characteristic 0, every reductive Lie algebra (one that is a sum of abelian and simple Lie algebras) has a non-degenerate invariant symmetric bilinear form. However the converse is false: a Lie algebra with a non-degenerate invariant symmetric bilinear form need not be a sum of simple and abelian Lie algebras. A typical counterexample is G = L[t]/tnL[t] where n>1, L is a simple complex Lie algebra with a bilinear form , and the bilinear form on G is given by taking the coefficient of tn−1 of the C[t]-valued bilinear form on G induced by the form on L. The bilinear form is non-degenerate, but the Lie algebra is not a sum of simple and abelian Lie algebras.