
Bidiagonal matrix
Encyclopedia
A bidiagonal matrix is a matrix with non-zero entries along the main diagonal and either the diagonal above or the diagonal below.
So that means there are two non zero diagonal in the matrix.
When the diagonal above the main diagonal has the non-zero entries the matrix is upper bidiagonal. When the diagonal below the main diagonal has the non-zero entries the matrix is lower bidiagonal.
For example, the following matrix is upper bidiagonal: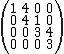
and the following matrix is lower bidiagonal:
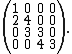
starts with reducing a general matrix into a bidiagonal one.
and the Singular value decomposition
uses this method as well.
So that means there are two non zero diagonal in the matrix.
When the diagonal above the main diagonal has the non-zero entries the matrix is upper bidiagonal. When the diagonal below the main diagonal has the non-zero entries the matrix is lower bidiagonal.
For example, the following matrix is upper bidiagonal:
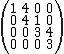
and the following matrix is lower bidiagonal:
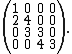
Usage
One variant of the QR algorithmQR algorithm
In numerical linear algebra, the QR algorithm is an eigenvalue algorithm: that is, a procedure to calculate the eigenvalues and eigenvectors of a matrix. The QR transformation was developed in the late 1950s by John G.F. Francis and by Vera N. Kublanovskaya , working independently...
starts with reducing a general matrix into a bidiagonal one.
and the Singular value decomposition
Singular value decomposition
In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
uses this method as well.
See also
- Diagonal matrixDiagonal matrixIn linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
- List of matrices
- LAPACKLAPACK-External links:* : a modern replacement for PLAPACK and ScaLAPACK* on Netlib.org* * * : a modern replacement for LAPACK that is MultiGPU ready* on Sourceforge.net* * optimized LAPACK for Solaris OS on SPARC/x86/x64 and Linux* * *...
- BidiagonalizationBidiagonalizationBidiagonalization is one of unitary matrix decompositions such that U* A V = B, where U and V are unitary matrices; * denotes Hermitian transpose; and B is upper bidiagonal...
- Hessenberg form The Hessenberg form is similar, but has more non zero diagonal lines than 2.
- Tridiagonal matrix with three diagonals
External links
- High performance algorithms for reduction to condensed (Hessenberg, tridiagonal, bidiagonal) form

