
Bertrand's box paradox
Encyclopedia
Bertrand's box paradox is a classic paradox
of elementary probability theory
. It was first posed by Joseph Bertrand in his Calcul des probabilités, published in 1889.
There are three boxes:
After choosing a box at random and withdrawing one coin at random, if that happens to be a gold coin, it may seem that the probability that the remaining coin is gold has a probability
of ; in fact, the probability is actually . Two problems that are logically equivalent are the Monty Hall problem and the
Three Prisoners problem
.
In a 1950 article, Warren Weaver
introduced a simple way to conduct the experiment on people: the boxes are replaced by cards, and gold and silver coins are replaced by red and black markings, one marking placed on each of the two faces of each card. In what Martin Gardner
has called the three-card swindle, a card is drawn from a hat, and if a red mark is shown, the dealer bets the victim even money that the other side is also red. The victim is convinced that the bet is fair, but the dealer makes money in the long run by winning of the time.
It's best to think of it as a total of 6 boxes at the beginning...
Box 1 has red coin A first and red coin B second
Box 2 has red coin B first and red coin A second
Box 3 has red coin A first and black coin B second
Box 4 has black coin B first and red coin A second
Box 5 has black coin A first and black coin B second
Box 6 has black coin B first and black coin A second
Box 1 represents 1 side of the first card and box 2 represents the other side.
Same goes for the second card using box 3 and 4...
And again for the third card using box 5 and 6.
Meaning if the person first draws a black coin, that means that it could be:
black coin A and black coin B is in there (1st option)
black coin B and black coin A is in there (2nd option)
black coin B and red coin A is in there (3rd option)
Therefore by saying the other coin is black (same color as first choice), you have 2/3 chance of getting it right.
These simple but slightly counterintuitive puzzles are used as a standard example in teaching probability theory. Their solution illustrates some basic principles, including the Kolmogorov axioms.
The problem can appear to be a true paradox
, because the same solution technique produces two different answers.
Probability :
Probability :
The problem can be shown to be equivalent to asking the question "What is the probability that I will pick a box with coins of the same colour?" This can be easily shown to be a probability of . When the first coin is shown to be gold, the probability that the second coin must be gold must also be , because the value of the first coin is independent of the second.
Bertrand's point in constructing this example, was that merely counting cases is not always proper. Instead, one should sum the probabilities that the cases would produce the observed result; and the two methods are equivalent if this probability is either 1 or 0 in every case. This condition is true in the second solution method, but not in the first. The correct way to solve the problem by treating the boxes as the individual cases is:
Alternatively, the chosen box has two coins of the same type of the time. So regardless of what kind of coin is in the chosen drawer, the box has two coins of that type of the time.
All the cards are placed into a hat and one is pulled at random and placed on a table. The side facing up is black. What are the odds that the other side is also black?
The answer is that the other side is black with probability . However, common intuition suggests a probability of either because there are two cards with black on them that this card could be, or because there are 3 white and 3 black sides and many people forget to eliminate the possibility of the "white card" in this situation (i.e. the card they flipped CANNOT be the "white card" because a black side was turned over).
In a survey of 53 Psychology freshmen taking an introductory probability course, 35 incorrectly responded ; only 3 students correctly responded .
Another presentation of the problem is to say : pick a random card out of the three, what are the odds that it has the same color on the other side ? Since only one card is mixed and two have the same color on their sides, it is easier to understand that the probability is . Also note that saying that the color is black (or the coin is gold) instead of white doesn't matter since it is symmetric: the answer is the same for white. So is the answer for the generic question 'same color on both sides'.
to the events of drawing each of the six faces of the three cards. These probabilities could conceivably be very different; perhaps the white card is larger than the black card, or the black side of the mixed card is heavier than the white side. The statement of the question does not explicitly address these concerns. The only constraints implied by the Kolmogorov axioms are that the probabilities are all non-negative, and they sum to 1.
The custom in problems when one literally pulls objects from a hat is to assume that all the drawing probabilities are equal. This forces the probability of drawing each side to be , and so the probability of drawing a given card is . In particular, the probability of drawing the double-white card is , and the probability of drawing a different card is .
In question, however, one has already selected a card from the hat and it shows a black face. At first glance it appears that there is a 50/50 chance (i.e. probability ) that the other side of the card is black, since there are two cards it might be: the black and the mixed. However, this reasoning fails to exploit all of the information; one knows not only that the card on the table has at least one black face, but also that in the population it was selected from, only 1 of the 3 black faces was on the mixed card.
An easy explanation is that to name the black sides as x, y and z where x and y are on the same card while z is on the mixed card, then the probability is divided on the 3 black sides with each. thus the probability that we chose either x or y is the sum of their probabilities thus .
Another way of thinking about it is that the problem is not about the chance that the other side is black, it's about the chance that you drew the all black card. If you drew a black face, then it's twice as likely that that face belongs to the black card than the mixed card.
Alternately, it can be seen as a bet not on a particular color, but a bet that the sides match. Betting on a particular color regardless of the face shown, will always have a chance of . However, betting that the sides match is , because 2 cards match and 1 does not.
, the conditional probability of having drawn the black card, given that a black face is showing, is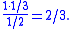
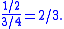
the chosen card is black or white, which chooses 2 of the 3 cards. Symmetry
suggests that the probability
is independent of the color chosen, so that the information about which color is shown does not affect the odds that both sides have the same color. (This argument can be formalized, but requires more advanced mathematics than yet discussed.)
Note the logical fact that the B/B card contributes significantly more (in fact twice) to the number of times "B" is on top. With the card B/W there is always a 50% chance W being on top, thus in 50% of the cases card B/W is drawn, the draw affects neither numerator nor denominator and effectively does not count (this is also true for all times W/W is drawn, so that card might as well be removed from the set altogether). Conclusively, the cards B/B and B/W are not of equal chances, because in the 50% of the cases B/W is drawn, this card is simply "disqualified".
Paradox
Similar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...
of elementary probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
. It was first posed by Joseph Bertrand in his Calcul des probabilités, published in 1889.
There are three boxes:
- a box containing two gold coins,
- a box with two silver coins, and
- a box with one of each.
After choosing a box at random and withdrawing one coin at random, if that happens to be a gold coin, it may seem that the probability that the remaining coin is gold has a probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
of ; in fact, the probability is actually . Two problems that are logically equivalent are the Monty Hall problem and the
Three Prisoners problem
Three Prisoners Problem
The Three Prisoners problem appeared in Martin Gardner's Mathematical Games column in Scientific American in 1959. It is mathematically equivalent to the Monty Hall problem with car and goat replaced with freedom and execution respectively, and also equivalent to, and presumably based on,...
.
In a 1950 article, Warren Weaver
Warren Weaver
Warren Weaver was an American scientist, mathematician, and science administrator...
introduced a simple way to conduct the experiment on people: the boxes are replaced by cards, and gold and silver coins are replaced by red and black markings, one marking placed on each of the two faces of each card. In what Martin Gardner
Martin Gardner
Martin Gardner was an American mathematics and science writer specializing in recreational mathematics, but with interests encompassing micromagic, stage magic, literature , philosophy, scientific skepticism, and religion...
has called the three-card swindle, a card is drawn from a hat, and if a red mark is shown, the dealer bets the victim even money that the other side is also red. The victim is convinced that the bet is fair, but the dealer makes money in the long run by winning of the time.
It's best to think of it as a total of 6 boxes at the beginning...
Box 1 has red coin A first and red coin B second
Box 2 has red coin B first and red coin A second
Box 3 has red coin A first and black coin B second
Box 4 has black coin B first and red coin A second
Box 5 has black coin A first and black coin B second
Box 6 has black coin B first and black coin A second
Box 1 represents 1 side of the first card and box 2 represents the other side.
Same goes for the second card using box 3 and 4...
And again for the third card using box 5 and 6.
Meaning if the person first draws a black coin, that means that it could be:
black coin A and black coin B is in there (1st option)
black coin B and black coin A is in there (2nd option)
black coin B and red coin A is in there (3rd option)
Therefore by saying the other coin is black (same color as first choice), you have 2/3 chance of getting it right.
These simple but slightly counterintuitive puzzles are used as a standard example in teaching probability theory. Their solution illustrates some basic principles, including the Kolmogorov axioms.
Box version
There are three boxes, each with one drawer on each of two sides. Each drawer contains a coin. One box has a gold coin on each side (GG), one a silver coin on each side (SS), and the other a gold coin on one side and a silver coin on the other (GS). A box is chosen at random, a random drawer is opened, and a gold coin is found inside it. What is the chance of the coin on the other side being gold?The problem can appear to be a true paradox
Paradox
Similar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...
, because the same solution technique produces two different answers.
Probability :
- Originally, all three boxes were equally likely to be chosen.
- The chosen box cannot be box SS
- So it must be from box GG or GS.
- The two remaining possibilities are equally likely, so the probability the box is GG is .
Probability :
- Originally, all six coins were equally likely to be chosen.
- The chosen coin cannot be from drawer S of box GS, or from either drawer of box SS.
- So it must come from the G drawer of box GS, or either drawer of box GG.
- The three remaining possibilities are equally likely, so the probability the drawer is from box is GG is .
The problem can be shown to be equivalent to asking the question "What is the probability that I will pick a box with coins of the same colour?" This can be easily shown to be a probability of . When the first coin is shown to be gold, the probability that the second coin must be gold must also be , because the value of the first coin is independent of the second.
Bertrand's point in constructing this example, was that merely counting cases is not always proper. Instead, one should sum the probabilities that the cases would produce the observed result; and the two methods are equivalent if this probability is either 1 or 0 in every case. This condition is true in the second solution method, but not in the first. The correct way to solve the problem by treating the boxes as the individual cases is:
- Originally, all three boxes were equally likely to be chosen.
- The probability the GG would produce a gold coin is 1.
- The probability the SS would produce a gold coin is 0.
- The probability the GS would produce a gold coin is .
- So the probability the chosen box is GG is ==.
Alternatively, the chosen box has two coins of the same type of the time. So regardless of what kind of coin is in the chosen drawer, the box has two coins of that type of the time.
Card version
Suppose there are three cards:- A black card that is black on both sides,
- A white card that is white on both sides, and
- A mixed card that is black on one side and white on the other.
All the cards are placed into a hat and one is pulled at random and placed on a table. The side facing up is black. What are the odds that the other side is also black?
The answer is that the other side is black with probability . However, common intuition suggests a probability of either because there are two cards with black on them that this card could be, or because there are 3 white and 3 black sides and many people forget to eliminate the possibility of the "white card" in this situation (i.e. the card they flipped CANNOT be the "white card" because a black side was turned over).
In a survey of 53 Psychology freshmen taking an introductory probability course, 35 incorrectly responded ; only 3 students correctly responded .
Another presentation of the problem is to say : pick a random card out of the three, what are the odds that it has the same color on the other side ? Since only one card is mixed and two have the same color on their sides, it is easier to understand that the probability is . Also note that saying that the color is black (or the coin is gold) instead of white doesn't matter since it is symmetric: the answer is the same for white. So is the answer for the generic question 'same color on both sides'.
Preliminaries
To solve the problem, either formally or informally, one must assign probabilitiesProbability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
to the events of drawing each of the six faces of the three cards. These probabilities could conceivably be very different; perhaps the white card is larger than the black card, or the black side of the mixed card is heavier than the white side. The statement of the question does not explicitly address these concerns. The only constraints implied by the Kolmogorov axioms are that the probabilities are all non-negative, and they sum to 1.
The custom in problems when one literally pulls objects from a hat is to assume that all the drawing probabilities are equal. This forces the probability of drawing each side to be , and so the probability of drawing a given card is . In particular, the probability of drawing the double-white card is , and the probability of drawing a different card is .
In question, however, one has already selected a card from the hat and it shows a black face. At first glance it appears that there is a 50/50 chance (i.e. probability ) that the other side of the card is black, since there are two cards it might be: the black and the mixed. However, this reasoning fails to exploit all of the information; one knows not only that the card on the table has at least one black face, but also that in the population it was selected from, only 1 of the 3 black faces was on the mixed card.
An easy explanation is that to name the black sides as x, y and z where x and y are on the same card while z is on the mixed card, then the probability is divided on the 3 black sides with each. thus the probability that we chose either x or y is the sum of their probabilities thus .
Intuition
Intuition tells one that one is choosing a card at random. However, one is actually choosing a face at random. There are 6 faces, of which 3 faces are white and 3 faces are black. Two of the 3 black faces belong to the same card. The chance of choosing one of those 2 faces is . Therefore, the chance of flipping the card over and finding another black face is also .Another way of thinking about it is that the problem is not about the chance that the other side is black, it's about the chance that you drew the all black card. If you drew a black face, then it's twice as likely that that face belongs to the black card than the mixed card.
Alternately, it can be seen as a bet not on a particular color, but a bet that the sides match. Betting on a particular color regardless of the face shown, will always have a chance of . However, betting that the sides match is , because 2 cards match and 1 does not.
Labels
One solution method is to label the card faces, for example numbers 1 through 6. Label the faces of the black card 1 and 2; label the faces of the mixed card 3 (black) and 4 (white); and label the faces of the white card 5 and 6. The observed black face could be 1, 2, or 3, all equally likely; if it is 1 or 2, the other side is black, and if it is 3, the other side is white. The probability that the other side is black is .Bayes' theorem
Given that the shown face is black, the other face is black if and only if the card is the black card. If the black card is drawn, a black face is shown with probability 1. The total probability of seeing a black face is ; the total probability of drawing the black card is . By Bayes' theoremBayes' theorem
In probability theory and applications, Bayes' theorem relates the conditional probabilities P and P. It is commonly used in science and engineering. The theorem is named for Thomas Bayes ....
, the conditional probability of having drawn the black card, given that a black face is showing, is
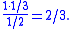
Eliminating the white card
Although the incorrect solution reasons that the white card is eliminated, one can also use that information in a correct solution. Modifying the previous method, given that the white card is not drawn, the probability of seeing a black face is , and the probability of drawing the black card is . The conditional probability of having drawn the black card, given that a black face is showing, is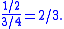
Symmetry
The probability (without considering the individual colors) that the hidden color is the same as the displayed color is clearly , as this holds if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the chosen card is black or white, which chooses 2 of the 3 cards. Symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
suggests that the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
is independent of the color chosen, so that the information about which color is shown does not affect the odds that both sides have the same color. (This argument can be formalized, but requires more advanced mathematics than yet discussed.)
Experiment
Using specially constructed cards, the choice can be tested a number of times. By constructing a fraction with the denominator being the number of times "B" is on top, and the numerator being the number of times both sides are "B", the experimenter will probably find the ratio to be near .Note the logical fact that the B/B card contributes significantly more (in fact twice) to the number of times "B" is on top. With the card B/W there is always a 50% chance W being on top, thus in 50% of the cases card B/W is drawn, the draw affects neither numerator nor denominator and effectively does not count (this is also true for all times W/W is drawn, so that card might as well be removed from the set altogether). Conclusively, the cards B/B and B/W are not of equal chances, because in the 50% of the cases B/W is drawn, this card is simply "disqualified".
Related problems
- Boy or Girl paradox
- Three Prisoners problemThree Prisoners ProblemThe Three Prisoners problem appeared in Martin Gardner's Mathematical Games column in Scientific American in 1959. It is mathematically equivalent to the Monty Hall problem with car and goat replaced with freedom and execution respectively, and also equivalent to, and presumably based on,...
- Two envelopes problemTwo envelopes problemThe two envelopes problem, also known as the exchange paradox, is a brain teaser, puzzle or paradox in logic, philosophy, probability and recreational mathematics, of special interest in decision theory and for the Bayesian interpretation of probability theory...
- Sleeping Beauty problemSleeping Beauty problemThe Sleeping Beauty problem is a puzzle in probability theory and formal epistemology in which an ideally rational epistemic agent is to be wakened once or twice according to the toss of a coin, and asked her degree of belief for the coin having come up heads....

