Bernstein inequalities (probability theory)
Encyclopedia
In probability theory
, Bernstein inequalities give bounds on the probability that the sum of random variables deviates from its mean. In the simplest case, let X1, ..., Xn be independent Bernoulli random variables taking values +1 and −1 with probability 1/2, then for every positive
,
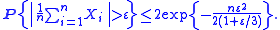
Bernstein inequalities were proved and published by Sergei Bernstein in the 1920s and 1930s.
Later, these inequalities were rediscovered several times in various forms. Thus, special cases of the Bernstein inequalities are also known as the Chernoff bound
, Hoeffding's inequality
and Azuma's inequality.
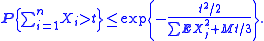
2. Let X1, ..., Xn be independent random variables. Suppose that for some positive real L and every integer k > 1,
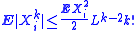
Then
3. Let X1, ..., Xn be independent random variables. Suppose that
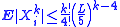
for all integer k > 3. Denote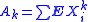
. Then,
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, Bernstein inequalities give bounds on the probability that the sum of random variables deviates from its mean. In the simplest case, let X1, ..., Xn be independent Bernoulli random variables taking values +1 and −1 with probability 1/2, then for every positive
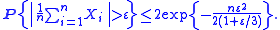
,Bernstein inequalities were proved and published by Sergei Bernstein in the 1920s and 1930s.
Later, these inequalities were rediscovered several times in various forms. Thus, special cases of the Bernstein inequalities are also known as the Chernoff bound
Chernoff bound
In probability theory, the Chernoff bound, named after Herman Chernoff, gives exponentially decreasing bounds on tail distributions of sums of independent random variables...
, Hoeffding's inequality
Hoeffding's inequality
In probability theory, Hoeffding's inequality provides an upper bound on the probability for the sum of random variables to deviate from its expected value. Hoeffding's inequality was proved by Wassily Hoeffding.LetX_1, \dots, X_n \!...
and Azuma's inequality.
Some of the inequalities
1. Let X1, ..., Xn be independent zero-mean random variables. Suppose that |X i| ≤ M almost surely, for all i. Then, for all positive t,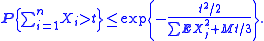2. Let X1, ..., Xn be independent random variables. Suppose that for some positive real L and every integer k > 1,
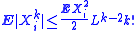
Then
3. Let X1, ..., Xn be independent random variables. Suppose that
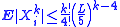
for all integer k > 3. Denote
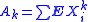. Then,-
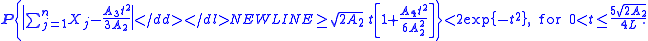
4. Bernstein also proved generalizations of the inequalities above to weakly dependent random variables. For example, inequality (2) can be extended as follows. Let X1, ..., Xn be possibly non-independent random variables. Suppose that for all integer i > 0,
-
-
-
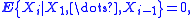
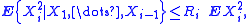
Then
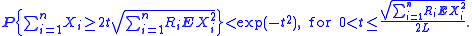
Proofs
The proofs are based on an application of Markov's inequalityMarkov's inequalityIn probability theory, Markov's inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant...
to the random variable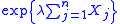
, for a suitable choice of the parameter 
.
See also
- McDiarmid's inequality
- Markov inequality
- Hoeffding's inequalityHoeffding's inequalityIn probability theory, Hoeffding's inequality provides an upper bound on the probability for the sum of random variables to deviate from its expected value. Hoeffding's inequality was proved by Wassily Hoeffding.LetX_1, \dots, X_n \!...
- Chebyshev's inequalityChebyshev's inequalityIn probability theory, Chebyshev’s inequality guarantees that in any data sample or probability distribution,"nearly all" values are close to the mean — the precise statement being that no more than 1/k2 of the distribution’s values can be more than k standard deviations away from the mean...
- Azuma's inequality
- Bennett's inequalityBennett's inequalityIn probability theory, Bennett's inequality provides an upper bound on the probability that the sum of independent random variables deviates from its expected value by more than any specified amount...
-