Chernoff bound
Encyclopedia
In probability theory
, the Chernoff bound, named after Herman Chernoff
, gives exponentially decreasing bounds on tail distributions of sums of independent random variables. It is better than the first or second moment based tail bounds such as Markov's inequality
or Chebyshev inequality, which only yield power-law bounds on tail decay.
It is related to the (historically earliest) Bernstein inequalities, and to Hoeffding's inequality
.
Let X1, ..., Xn be independent Bernoulli random variables, each having probability p > 1/2. Then the probability of simultaneous occurrence of more than n/2 of the events has an exact value P, where
has an exact value P, where

The Chernoff bound shows that P has the following lower bound:

This result admits various generalisations as outlined below. One can encounter many flavours of Chernoff bounds: the original additive form (which gives a bound on the absolute error
) or the more practical multiplicative form (which bounds the error relative
to the mean).
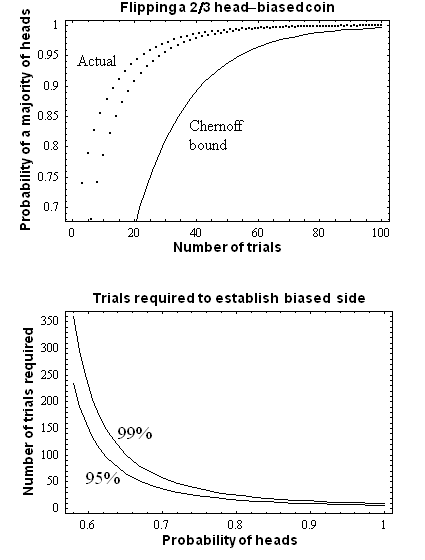
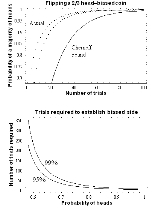
The simplest case of Chernoff bounds is used to bound the success probability of majority agreement for n independent, equally likely events.
A simple motivating example is to consider a biased coin. One side (say, Heads), is more likely to come up than the other, but you don't know which and would like to find out. The obvious solution is to flip it many times and then choose the side that comes up the most. But how many times do you have to flip it to be confident that you've chosen correctly?
In our example, let denote the event that the ith coin flip comes up Heads; suppose that we want to ensure we choose the wrong side with at most a small probability ε. Then, rearranging the above, we must have:
denote the event that the ith coin flip comes up Heads; suppose that we want to ensure we choose the wrong side with at most a small probability ε. Then, rearranging the above, we must have:

If the coin is noticeably biased, say coming up on one side 60% of the time (p = .6), then we can guess that side with 95% ( ) accuracy after 150 flips
) accuracy after 150 flips . If it is 90% biased, then a mere 10 flips suffices. If the coin is only biased a tiny amount, like most real coins are, the number of necessary flips becomes much larger.
. If it is 90% biased, then a mere 10 flips suffices. If the coin is only biased a tiny amount, like most real coins are, the number of necessary flips becomes much larger.
More practically, the Chernoff bound is used in randomized algorithm
s (or in computational devices such as quantum computer
s) to determine a bound on the number of runs necessary to determine a value by majority agreement, up to a specified probability. For example, suppose an algorithm (or machine) A computes the correct value of a function f with probability p > 1/2. If we choose n satisfying the inequality above, the probability that a majority exists and is equal to the correct value is at least 1 − ε, which for small enough ε is quite reliable. If p is a constant, ε diminishes exponentially with growing n, which is what makes algorithms in the complexity class BPP efficient.
Notice that if p is very close to 1/2, the necessary n can become very large. For example, if p = 1/2 + 1/2m, as it might be in some PP
algorithms, the result is that n is bounded below by an exponential function in m:

 , is obtained by applying etX for some well-chosen value of t. This method was first applied by Sergei Bernstein to prove the related Bernstein inequalities.
, is obtained by applying etX for some well-chosen value of t. This method was first applied by Sergei Bernstein to prove the related Bernstein inequalities.
From Markov's inequality
and using independence we can derive the following useful inequality:
For any t > 0,
In particular optimizing over t and using independence we obtain,
Similarly,
and so,
and hence is called Chernoff-Hoeffding theorem.
Assume random variables are i.i.d.
are i.i.d.
Let ,
,  , and
, and  .
.
Then
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, the Chernoff bound, named after Herman Chernoff
Herman Chernoff
Herman Chernoff is an American applied mathematician, statistician and physicist formerly a professor at MIT and currently working at Harvard University.-Education:* Ph.D., Applied Mathematics, 1948. Brown University....
, gives exponentially decreasing bounds on tail distributions of sums of independent random variables. It is better than the first or second moment based tail bounds such as Markov's inequality
Markov's inequality
In probability theory, Markov's inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant...
or Chebyshev inequality, which only yield power-law bounds on tail decay.
It is related to the (historically earliest) Bernstein inequalities, and to Hoeffding's inequality
Hoeffding's inequality
In probability theory, Hoeffding's inequality provides an upper bound on the probability for the sum of random variables to deviate from its expected value. Hoeffding's inequality was proved by Wassily Hoeffding.LetX_1, \dots, X_n \!...
.
Let X1, ..., Xn be independent Bernoulli random variables, each having probability p > 1/2. Then the probability of simultaneous occurrence of more than n/2 of the events
 has an exact value P, where
has an exact value P, where
The Chernoff bound shows that P has the following lower bound:

This result admits various generalisations as outlined below. One can encounter many flavours of Chernoff bounds: the original additive form (which gives a bound on the absolute error
Approximation error
The approximation error in some data is the discrepancy between an exact value and some approximation to it. An approximation error can occur because#the measurement of the data is not precise due to the instruments...
) or the more practical multiplicative form (which bounds the error relative
Approximation error
The approximation error in some data is the discrepancy between an exact value and some approximation to it. An approximation error can occur because#the measurement of the data is not precise due to the instruments...
to the mean).
A motivating example

The simplest case of Chernoff bounds is used to bound the success probability of majority agreement for n independent, equally likely events.
A simple motivating example is to consider a biased coin. One side (say, Heads), is more likely to come up than the other, but you don't know which and would like to find out. The obvious solution is to flip it many times and then choose the side that comes up the most. But how many times do you have to flip it to be confident that you've chosen correctly?
In our example, let
 denote the event that the ith coin flip comes up Heads; suppose that we want to ensure we choose the wrong side with at most a small probability ε. Then, rearranging the above, we must have:
denote the event that the ith coin flip comes up Heads; suppose that we want to ensure we choose the wrong side with at most a small probability ε. Then, rearranging the above, we must have:
If the coin is noticeably biased, say coming up on one side 60% of the time (p = .6), then we can guess that side with 95% (
 ) accuracy after 150 flips
) accuracy after 150 flips . If it is 90% biased, then a mere 10 flips suffices. If the coin is only biased a tiny amount, like most real coins are, the number of necessary flips becomes much larger.
. If it is 90% biased, then a mere 10 flips suffices. If the coin is only biased a tiny amount, like most real coins are, the number of necessary flips becomes much larger.More practically, the Chernoff bound is used in randomized algorithm
Randomized algorithm
A randomized algorithm is an algorithm which employs a degree of randomness as part of its logic. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random bits...
s (or in computational devices such as quantum computer
Quantum computer
A quantum computer is a device for computation that makes direct use of quantum mechanical phenomena, such as superposition and entanglement, to perform operations on data. Quantum computers are different from traditional computers based on transistors...
s) to determine a bound on the number of runs necessary to determine a value by majority agreement, up to a specified probability. For example, suppose an algorithm (or machine) A computes the correct value of a function f with probability p > 1/2. If we choose n satisfying the inequality above, the probability that a majority exists and is equal to the correct value is at least 1 − ε, which for small enough ε is quite reliable. If p is a constant, ε diminishes exponentially with growing n, which is what makes algorithms in the complexity class BPP efficient.
Notice that if p is very close to 1/2, the necessary n can become very large. For example, if p = 1/2 + 1/2m, as it might be in some PP
PP (complexity)
In complexity theory, PP is the class of decision problems solvable by a probabilistic Turing machine in polynomial time, with an error probability of less than 1/2 for all instances. The abbreviation PP refers to probabilistic polynomial time...
algorithms, the result is that n is bounded below by an exponential function in m:

The first step in the proof of Chernoff bounds
The Chernoff bound for a random variable X, which is the sum of n independent random variables , is obtained by applying etX for some well-chosen value of t. This method was first applied by Sergei Bernstein to prove the related Bernstein inequalities.
, is obtained by applying etX for some well-chosen value of t. This method was first applied by Sergei Bernstein to prove the related Bernstein inequalities.From Markov's inequality
Markov's inequality
In probability theory, Markov's inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant...
and using independence we can derive the following useful inequality:
For any t > 0,
In particular optimizing over t and using independence we obtain,
Similarly,
and so,
Theorem for additive form (absolute error)
The following Theorem is due to Wassily HoeffdingWassily Hoeffding
Wassily Hoeffding was an American statistician and probabilist...
and hence is called Chernoff-Hoeffding theorem.
Assume random variables
 are i.i.d.
are i.i.d.Let
 ,
,  , and
, and  .
.Then
-

and-

where-

is the Kullback-Leibler divergence between Bernoulli distributed random variables with parameters and
and  respectively. If
respectively. If  , then
, then 
Proof
The proof starts from the general inequality (+) above. . Taking a = mq in (+), we obtain:
. Taking a = mq in (+), we obtain:
-

Now, knowing that ,
,  , we have
, we have
-

Therefore we can easily compute the infimum, using calculus and some logarithms. Thus,-

Setting the last equation to zero and solving, we have-

so that .
.
Thus, .
.
As , we see that
, we see that  , so our bound is satisfied on
, so our bound is satisfied on  . Having solved for
. Having solved for  , we can plug back into the equations above to find that
, we can plug back into the equations above to find that
-

We now have our desired result, that-

To complete the proof for the symmetric case, we simply define the random variable , apply the same proof, and plug it into our bound.
, apply the same proof, and plug it into our bound.
Simpler bounds
A simpler bound follows by relaxing the theorem using
 , which follows from the convexityConvex functionIn mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
, which follows from the convexityConvex functionIn mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
of and the fact that
and the fact that  . This results in a special case of Hoeffding's inequalityHoeffding's inequalityIn probability theory, Hoeffding's inequality provides an upper bound on the probability for the sum of random variables to deviate from its expected value. Hoeffding's inequality was proved by Wassily Hoeffding.LetX_1, \dots, X_n \!...
. This results in a special case of Hoeffding's inequalityHoeffding's inequalityIn probability theory, Hoeffding's inequality provides an upper bound on the probability for the sum of random variables to deviate from its expected value. Hoeffding's inequality was proved by Wassily Hoeffding.LetX_1, \dots, X_n \!...
.
Sometimes, the bound
 for
for  , which is stronger for
, which is stronger for  , is also used.
, is also used.
Theorem for multiplicative form of Chernoff bound (relative error)
Let random variables be independentStatistical independenceIn probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
be independentStatistical independenceIn probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
random variables taking on values 0 or 1. Further, assume that . Then, if we let
. Then, if we let  and
and  be the expectation of
be the expectation of  , for any
, for any 
-

Proof
According to (+),-

The third line above follows because takes the value
takes the value  with probability
with probability  and the value
and the value  with probability
with probability  . This is identical to the calculation above in the proof of the Theorem for additive form (absolute error).
. This is identical to the calculation above in the proof of the Theorem for additive form (absolute error).
Rewriting as
as  and recalling that
and recalling that  (with strict inequality if
(with strict inequality if  ), we set
), we set  . The same result can be obtained by directly replacing a in the equation for the Chernoff bound with
. The same result can be obtained by directly replacing a in the equation for the Chernoff bound with  .
.
Thus,-

If we simply set so that
so that  for
for  , we can substitute and find
, we can substitute and find
-

This proves the result desired. A similar proof strategy can be used to show that-

Better Chernoff bounds for some special cases
We can obtain stronger bounds using simpler proof techniques for some special cases of symmetric random variables.
Let be independent random variables,
be independent random variables,
-
 .
.
(a) .
.
Then,-
 ,
,
and therefore also .
.
(b)
Then, ,
, ,
, ,
, .
.
Applications of Chernoff bound
Chernoff bounds have very useful applications in set balancing and packet routingRoutingRouting is the process of selecting paths in a network along which to send network traffic. Routing is performed for many kinds of networks, including the telephone network , electronic data networks , and transportation networks...
in sparse networks.
The set balancing problem arises while designing statistical experiments. Typically while designing a statistical experiment, given the features of each participant in the experiment, we need to know how to divide the participants into 2 disjoint groups such that each feature is roughly as balanced as possible between the two groups. Refer to this book section for more info on the problem.
Chernoff bounds are also used to obtain tight bounds for permutation routing problems which reduce network congestionNetwork congestionIn data networking and queueing theory, network congestion occurs when a link or node is carrying so much data that its quality of service deteriorates. Typical effects include queueing delay, packet loss or the blocking of new connections...
while routing packets in sparse networks. Refer to this book section for a thorough treatment of the problem.
Matrix Chernoff bound
Rudolf AhlswedeRudolf AhlswedeRudolf F. Ahlswede was a German mathematician. Born in Dielmissen, Germany, he studied mathematics, physics, and philosophy. He wrote his Ph.D. thesis in 1966, at the University of Göttingen, with the topic "Contributions to the Shannon information theory in case of non-stationary channels"...
and Andreas WinterAndreas WinterAndreas Winter is a mathematician at the University of Bristol and CQT at the National University of Singapore. He received his Ph.D...
introduced a Chernoff bound for matrix-valued random variables.
See also
- Bernstein inequalities (probability theory)
- Hoeffding's inequalityHoeffding's inequalityIn probability theory, Hoeffding's inequality provides an upper bound on the probability for the sum of random variables to deviate from its expected value. Hoeffding's inequality was proved by Wassily Hoeffding.LetX_1, \dots, X_n \!...
- Markov's inequalityMarkov's inequalityIn probability theory, Markov's inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant...
- Chebyshev's inequalityChebyshev's inequalityIn probability theory, Chebyshev’s inequality guarantees that in any data sample or probability distribution,"nearly all" values are close to the mean — the precise statement being that no more than 1/k2 of the distribution’s values can be more than k standard deviations away from the mean...
-
-
-
-
-
-
-
-
-
-
-
-
-
-





