
Ax-Grothendieck theorem
Encyclopedia
In mathematics, the Ax–Grothendieck theorem is a result about injectivity and surjectivity of polynomial
s that was proved independently by James Ax
and Alexander Grothendieck
.
The theorem is often given as the special case as follows: If P is a polynomial function from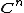 to
to 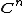 and P is injective then P is bijective. That is, if P is one-to-one then P is onto.
and P is injective then P is bijective. That is, if P is one-to-one then P is onto.
The full theorem generalizes to any algebraic variety
over an algebraically closed
field
.
s and their algebraic closure
s. That is, for any field F that is itself finite or that is the closure of a finite field, if a polynomial P from Fn to itself is injective then it is bijective.
If F is a finite field, then Fn is finite. In this case the theorem is true for trivial reasons having nothing to do with the representation of the function as a polynomial: any injection of a finite set to itself is a bijection. When F is the algebraic closure of a finite field, the result follows from Hilbert's Nullstellensatz
. The Ax–Grothendieck theorem for complex numbers can therefore be proven by showing that a counterexample over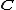 would translate into a counterexample in some algebraic extension of a finite field.
would translate into a counterexample in some algebraic extension of a finite field.
This method of proof is noteworthy in that it is an example of the idea that finitistic algebraic relations in fields of characteristic
0 translate into algebraic relations over finite fields with large characteristic. Thus, one can use the arithmetic of finite fields to prove a statement about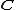 even though there is no non-trivial homomorphism
even though there is no non-trivial homomorphism
from any finite field to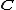 . The proof thus uses model theoretic principles
. The proof thus uses model theoretic principles
to prove an elementary statement about polynomials. The proof for the general case uses a similar method.
gave a proof using topology. The case of n = 1 and field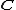 follows since
follows since 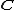 is algebraically closed and can also be thought of as a special case of the result that for any analytic function
is algebraically closed and can also be thought of as a special case of the result that for any analytic function
f on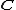 , injectivity of f implies surjectivity of f. This is a corollary of Picard's theorem
, injectivity of f implies surjectivity of f. This is a corollary of Picard's theorem
.
: There, it is proved that a radicial
S-endomorphism of a scheme X of finite type over S is bijective (10.4.11), and that if X/S is of finite presentation, and the endomorphism is a monomorphism, then it is an automorphism (17.9.6).
The Ax–Grothendieck theorem may also be used to prove the Garden of Eden theorem, a result that like the Ax–Grothendieck theorem relates injectivity with surjectivity but in cellular automata
rather than in algebraic fields. Although direct proofs of this theorem are known, the proof via the Ax–Grothendieck theorem extends more broadly, to automata acting on amenable group
s.
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s that was proved independently by James Ax
James Ax
James Burton Ax was a mathematician who proved several results in algebra and number theory by using model theory. He shared the seventh Frank Nelson Cole Prize in Number Theory with Simon B. Kochen, which was awarded for a series of three joint papers on Diophantine problems.James Ax earned his...
and Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
.
The theorem is often given as the special case as follows: If P is a polynomial function from
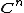 to
to 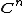 and P is injective then P is bijective. That is, if P is one-to-one then P is onto.
and P is injective then P is bijective. That is, if P is one-to-one then P is onto.The full theorem generalizes to any algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
over an algebraically closed
Algebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
.
Proof via finite fields
Grothendieck's proof of the theorem is based on proving the analogous theorem for finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s and their algebraic closure
Algebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
s. That is, for any field F that is itself finite or that is the closure of a finite field, if a polynomial P from Fn to itself is injective then it is bijective.
If F is a finite field, then Fn is finite. In this case the theorem is true for trivial reasons having nothing to do with the representation of the function as a polynomial: any injection of a finite set to itself is a bijection. When F is the algebraic closure of a finite field, the result follows from Hilbert's Nullstellensatz
Hilbert's Nullstellensatz
Hilbert's Nullstellensatz is a theorem which establishes a fundamental relationship between geometry and algebra. This relationship is the basis of algebraic geometry, an important branch of mathematics. It relates algebraic sets to ideals in polynomial rings over algebraically closed fields...
. The Ax–Grothendieck theorem for complex numbers can therefore be proven by showing that a counterexample over
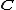 would translate into a counterexample in some algebraic extension of a finite field.
would translate into a counterexample in some algebraic extension of a finite field.This method of proof is noteworthy in that it is an example of the idea that finitistic algebraic relations in fields of characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
0 translate into algebraic relations over finite fields with large characteristic. Thus, one can use the arithmetic of finite fields to prove a statement about
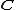 even though there is no non-trivial homomorphism
even though there is no non-trivial homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
from any finite field to
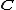 . The proof thus uses model theoretic principles
. The proof thus uses model theoretic principlesModel theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
to prove an elementary statement about polynomials. The proof for the general case uses a similar method.
Other proofs
There are other proofs of the theorem. Armand BorelArmand Borel
Armand Borel was a Swiss mathematician, born in La Chaux-de-Fonds, and was a permanent professor at the Institute for Advanced Study in Princeton, New Jersey, United States from 1957 to 1993...
gave a proof using topology. The case of n = 1 and field
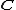 follows since
follows since 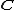 is algebraically closed and can also be thought of as a special case of the result that for any analytic function
is algebraically closed and can also be thought of as a special case of the result that for any analytic functionAnalytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
f on
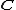 , injectivity of f implies surjectivity of f. This is a corollary of Picard's theorem
, injectivity of f implies surjectivity of f. This is a corollary of Picard's theoremPicard theorem
In complex analysis, the term Picard theorem refers to either of two distinct yet related theorems, both of which pertain to the range of an analytic function.-Little Picard:...
.
Related results
Another example of reducing theorems about morphisms of finite type to finite fields can be found in EGA IVÉléments de géométrie algébrique
The Éléments de géométrie algébrique by Alexander Grothendieck , or EGA for short, is a rigorous treatise, in French, on algebraic geometry that was published from 1960 through 1967 by the Institut des Hautes Études Scientifiques...
: There, it is proved that a radicial
Radicial morphism
In algebraic geometry, a domain in mathematics, a morphism of schemesis called radicial or universally injective, if, for every field K the induced map X → Y is injective...
S-endomorphism of a scheme X of finite type over S is bijective (10.4.11), and that if X/S is of finite presentation, and the endomorphism is a monomorphism, then it is an automorphism (17.9.6).
The Ax–Grothendieck theorem may also be used to prove the Garden of Eden theorem, a result that like the Ax–Grothendieck theorem relates injectivity with surjectivity but in cellular automata
Cellular automaton
A cellular automaton is a discrete model studied in computability theory, mathematics, physics, complexity science, theoretical biology and microstructure modeling. It consists of a regular grid of cells, each in one of a finite number of states, such as "On" and "Off"...
rather than in algebraic fields. Although direct proofs of this theorem are known, the proof via the Ax–Grothendieck theorem extends more broadly, to automata acting on amenable group
Amenable group
In mathematics, an amenable group is a locally compact topological group G carrying a kind of averaging operation on bounded functions that is invariant under translation by group elements...
s.

