Apéry's theorem
Encyclopedia
In mathematics
, Apéry's theorem is a result in number theory
that states the Apéry's constant
ζ(3) is irrational. That is, the number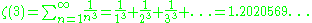
cannot be written as a fraction p/q with p and q being integers.
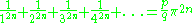
for some rational number p/q. Specifically, writing the infinite series on the left as ζ(2n) he showed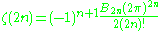
where the Bn are the rational Bernoulli numbers. Once it was proved that πn is always irrational this showed that ζ(2n) is irrational for all positive integers n.
No such representation in terms of π is known for the so-called odd zeta constants, the values ζ(2n+1) for positive integers n. It has been conjectured that the ratios of these quantities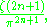
are transcendental for every integer n ≥ 1.
Because of this, no proof could be found to show that the odd zeta constants were irrational, even though they were—and still are—all believed to be transcendental
. However, in June 1978 Roger Apéry
gave a talk entitled "Sur l'irrationalité de ζ(3)." During the course of the talk he outlined proofs that ζ(3) and ζ(2) were irrational, the latter using methods simplified from those used to tackle the former rather than relying on the expression in terms of π. Due to the wholly unexpected nature of the result and Apéry's blasé and very sketchy approach to the subject many of the mathematicians in the audience dismissed the proof as flawed. Three of the audience members suspected Apéry was onto something, though, and set out to confirm his proof.
Two months later these three—Henri Cohen, Hendrik Lenstra
, and Alfred van der Poorten—finished their work, and on August 18 Cohen delivered a lecture giving full details of Apéry's proof. Following the talk Apéry himself took to the podium to explain the source of some of his ideas.
, which states that a number ξ is irrational if there are infinitely many coprime integers p and q such that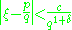
for some fixed c,δ>0.
The starting point for Apéry was the series representation of ζ(3) as
Roughly speaking, Apéry then defined a sequence cn,k which converges to ζ(3) about as fast as the above series, specifically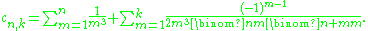
He then defined two more sequences an and bn that, roughly, have the quotient cn,k. These sequences were
and
The sequence an/bn converges to ζ(3) fast enough to apply the criterion, but unfortunately an is not an integer after n=2. Nevertheless, Apéry showed that even after multiplying an and bn by a suitable integer to cure this problem the convergence was still fast enough to guarantee irrationality.
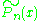. Using a representation that would later be generalized to Hadjicostas's formula
, Beukers showed that
for some integers An and Bn (sequences and ). Using partial integration and the assumption that ζ(3) was rational and equal to a/b, Beukers eventually derived the inequality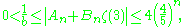
which is a contradiction since the right-most expression tends to zero and so must eventually fall below 1/b.
A more recent proof by Wadim Zudilin
is more reminiscent of Apéry's original proof, and also has similarities to a fourth proof by Yuri Nesterenko
. These later proofs again derive a contradiction from the assumption that ζ(3) is rational by constructing sequences that tend to zero but are bounded below by some positive constant. They are somewhat less transparent than the earlier proofs, relying as they do on hypergeometric series.
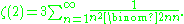
Due to the success of Apéry's method a search was undertaken for a number ξ5 with the property that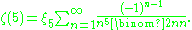
If such a ξ5 were found then the methods used to prove Apéry's theorem would be expected to work on a proof that ζ(5) is irrational. Unfortunately, extensive computer searching has failed to find such a constant, and in fact it is now known that if ξ5 exists and if it is an algebraic number of degree at most 25, then the coefficients in its minimal polynomial
must be enormous, at least 10383, so extending Apéry's proof to work on the higher odd zeta constants doesn't seem likely to work.
Despite this, many mathematicians working in this area expect a breakthrough sometime soon. Indeed, recent work by Wadim Zudilin
and Tanguy Rivoal has shown that infinitely many of the numbers ζ(2n+1) must be irrational, and even that at least one of the numbers ζ(5), ζ(7), ζ(9), and ζ(11) must be irrational. Their work uses linear forms in values of the zeta function and estimates upon them to bound the dimension of a vector space
spanned by values of the zeta function at odd integers. Hopes that Zudilin could cut his list further to just one number did not materialise, but work on this problem is still an active area of research. Higher zeta constants have application to physics: they describe correlation functions in quantum spin chains
, see for example.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Apéry's theorem is a result in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
that states the Apéry's constant
Apéry's constant
In mathematics, Apéry's constant is a number that occurs in a variety of situations. It arises naturally in a number of physical problems, including in the second- and third-order terms of the electron's gyromagnetic ratio using quantum electrodynamics...
ζ(3) is irrational. That is, the number
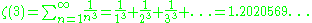
cannot be written as a fraction p/q with p and q being integers.
History
Euler proved in the eighteenth century that if n is a positive integer then we have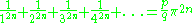for some rational number p/q. Specifically, writing the infinite series on the left as ζ(2n) he showed
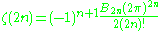
where the Bn are the rational Bernoulli numbers. Once it was proved that πn is always irrational this showed that ζ(2n) is irrational for all positive integers n.
No such representation in terms of π is known for the so-called odd zeta constants, the values ζ(2n+1) for positive integers n. It has been conjectured that the ratios of these quantities
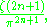
are transcendental for every integer n ≥ 1.
Because of this, no proof could be found to show that the odd zeta constants were irrational, even though they were—and still are—all believed to be transcendental
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
. However, in June 1978 Roger Apéry
Roger Apéry
Roger Apéry was a Greek-French mathematician most remembered for Apéry's theorem, that ζ is an irrational number where ζ denotes the Riemann zeta function....
gave a talk entitled "Sur l'irrationalité de ζ(3)." During the course of the talk he outlined proofs that ζ(3) and ζ(2) were irrational, the latter using methods simplified from those used to tackle the former rather than relying on the expression in terms of π. Due to the wholly unexpected nature of the result and Apéry's blasé and very sketchy approach to the subject many of the mathematicians in the audience dismissed the proof as flawed. Three of the audience members suspected Apéry was onto something, though, and set out to confirm his proof.
Two months later these three—Henri Cohen, Hendrik Lenstra
Hendrik Lenstra
Hendrik Willem Lenstra, Jr. is a Dutch mathematician.-Biography:Lenstra received his doctorate from the University of Amsterdam in 1977 and became a professor there in 1978...
, and Alfred van der Poorten—finished their work, and on August 18 Cohen delivered a lecture giving full details of Apéry's proof. Following the talk Apéry himself took to the podium to explain the source of some of his ideas.
Apéry's proof
Apéry's original proof was based on the well known irrationality criterion from DirichletJohann Peter Gustav Lejeune Dirichlet
Johann Peter Gustav Lejeune Dirichlet was a German mathematician with deep contributions to number theory , as well as to the theory of Fourier series and other topics in mathematical analysis; he is credited with being one of the first mathematicians to give the modern formal definition of a...
, which states that a number ξ is irrational if there are infinitely many coprime integers p and q such that
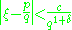
for some fixed c,δ>0.
The starting point for Apéry was the series representation of ζ(3) as
Roughly speaking, Apéry then defined a sequence cn,k which converges to ζ(3) about as fast as the above series, specifically
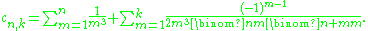
He then defined two more sequences an and bn that, roughly, have the quotient cn,k. These sequences were
and
The sequence an/bn converges to ζ(3) fast enough to apply the criterion, but unfortunately an is not an integer after n=2. Nevertheless, Apéry showed that even after multiplying an and bn by a suitable integer to cure this problem the convergence was still fast enough to guarantee irrationality.
Later proofs
Within a year of Apéry's result an alternative proof was found by Frits Beukers, who replaced Apéry's series with integrals involving the shifted Legendre polynomials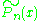. Using a representation that would later be generalized to Hadjicostas's formulaHadjicostas's formula
In mathematics, Hadjicostas's formula is a formula relating a certain double integral to values of the Gamma function and the Riemann zeta function.-Statement:Let s be a complex number with Re > −2...
, Beukers showed that
for some integers An and Bn (sequences and ). Using partial integration and the assumption that ζ(3) was rational and equal to a/b, Beukers eventually derived the inequality
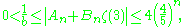
which is a contradiction since the right-most expression tends to zero and so must eventually fall below 1/b.
A more recent proof by Wadim Zudilin
Wadim Zudilin
Wadim Zudilin is a Russian number theorist who is active in studying hypergeometric functions and zeta constants. He studied under Yuri V. Nesterenko and worked at Moscow State University, the Steklov Institute of Mathematics and the Max Planck Institute for Mathematics. He now works at the...
is more reminiscent of Apéry's original proof, and also has similarities to a fourth proof by Yuri Nesterenko
Yuri Valentinovich Nesterenko
Yuri Valentinovich Nesterenko is a mathematician who has written papers in algebraic independence theory and transcendental number theory.In 1997 he was awarded the Ostrowski Prize for his proof that the numbers π and eπ are algebraically independent...
. These later proofs again derive a contradiction from the assumption that ζ(3) is rational by constructing sequences that tend to zero but are bounded below by some positive constant. They are somewhat less transparent than the earlier proofs, relying as they do on hypergeometric series.
Higher zeta constants
Apéry and Beukers could simplify their proofs to work on ζ(2) as well thanks to the series representation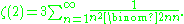Due to the success of Apéry's method a search was undertaken for a number ξ5 with the property that
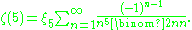
If such a ξ5 were found then the methods used to prove Apéry's theorem would be expected to work on a proof that ζ(5) is irrational. Unfortunately, extensive computer searching has failed to find such a constant, and in fact it is now known that if ξ5 exists and if it is an algebraic number of degree at most 25, then the coefficients in its minimal polynomial
Minimal polynomial (field theory)
In field theory, given a field extension E / F and an element α of E that is an algebraic element over F, the minimal polynomial of α is the monic polynomial p, with coefficients in F, of least degree such that p = 0...
must be enormous, at least 10383, so extending Apéry's proof to work on the higher odd zeta constants doesn't seem likely to work.
Despite this, many mathematicians working in this area expect a breakthrough sometime soon. Indeed, recent work by Wadim Zudilin
Wadim Zudilin
Wadim Zudilin is a Russian number theorist who is active in studying hypergeometric functions and zeta constants. He studied under Yuri V. Nesterenko and worked at Moscow State University, the Steklov Institute of Mathematics and the Max Planck Institute for Mathematics. He now works at the...
and Tanguy Rivoal has shown that infinitely many of the numbers ζ(2n+1) must be irrational, and even that at least one of the numbers ζ(5), ζ(7), ζ(9), and ζ(11) must be irrational. Their work uses linear forms in values of the zeta function and estimates upon them to bound the dimension of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
spanned by values of the zeta function at odd integers. Hopes that Zudilin could cut his list further to just one number did not materialise, but work on this problem is still an active area of research. Higher zeta constants have application to physics: they describe correlation functions in quantum spin chains
Heisenberg model (quantum)
The Heisenberg model is a statistical mechanical model used in the study of critical points and phase transitions of magnetic systems, in which the spin of the magnetic systems are treated quantum mechanically...
, see for example.