
Acyclic models theorem
Encyclopedia
In algebraic topology
, a discipline within mathematics
, the acyclic models theorem can be used to show that two homology theories are isomorphic. The theorem
was developed by topologists Samuel Eilenberg
and Saunders MacLane. They discovered that, when topologists were writing proofs to establish equivalence of various homology theories, there were numerous similarities in the processes. Eilenberg and MacLane then discovered the theorem to generalize this process.
It can be used to prove the Eilenberg–Zilber theorem
.
 be an arbitrary category
be an arbitrary category
and be the category of chain complexes of
be the category of chain complexes of  -module
-module
s. Let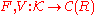 be covariant functors such that:
be covariant functors such that:
Then the following assertions hold:
version is the one that says that if is a complex of
is a complex of
projectives in an abelian category
and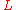 is an acyclic
is an acyclic
complex in that category, then any map extends to a chain map
extends to a chain map  , unique up to
, unique up to
homotopy.
This specializes almost to the above theorem if one uses the functor category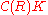 as the abelian category. Free functors are projective objects in that category. The morphisms in the functor category are natural transformations, so the constructed chain maps and homotopies are all natural. The difference is that in the above version,
as the abelian category. Free functors are projective objects in that category. The morphisms in the functor category are natural transformations, so the constructed chain maps and homotopies are all natural. The difference is that in the above version,  being acyclic is a stronger assumption than being acyclic only at certain objects.
being acyclic is a stronger assumption than being acyclic only at certain objects.
On the other hand, the above version almost implies this version by letting a category with only one object. Then the free functor
a category with only one object. Then the free functor  is basically just free (and hence projective) module.
is basically just free (and hence projective) module.  being acyclic at the models (there is only one) means nothing else than that the complex
being acyclic at the models (there is only one) means nothing else than that the complex  is acyclic.
is acyclic.
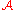 be an abelian category (for example
be an abelian category (for example  or
or 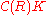 ). A class
). A class  of chain complexes over
of chain complexes over 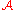 will be called an acyclic class provided:
will be called an acyclic class provided:
There are three natural examples of acyclic classes, although doubtless
others exist. The first is that of homotopy contractible complexes.
The second is that of acyclic complexes. In functor categories (e.g. the
category of all functors from topological spaces to abelian groups),
there is a class of complexes that are contractible on each object, but
where the contractions might not be given by natural transformations.
Another example is again in functor categories but this time the complexes are acyclic only at certain objects.
Let denote the class of chain maps between complexes
denote the class of chain maps between complexes
whose mapping cone belongs to . Although
. Although
 does not necessarily have a calculus of either right
does not necessarily have a calculus of either right
or left fractions, it has weaker properties of having homotopy classes
of both left and right fractions that permit forming the class
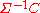 gotten by inverting the arrows in
gotten by inverting the arrows in
 .
.
Let be an augmented endofunctor on
be an augmented endofunctor on  ,
,
meaning there is given a natural transformation
 (the identity functor on
(the identity functor on  ). We say that the chain complex
). We say that the chain complex  is
is  -presentable if for each
-presentable if for each  , the chain
, the chain
complex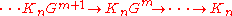
belongs to . The boundary operator is given by
. The boundary operator is given by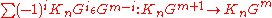 .
.
We say that the chain complex functor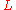 is
is
 -acyclic if the augmented chain complex
-acyclic if the augmented chain complex
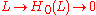 belongs to
belongs to  .
.
Theorem. Let be an acyclic class and
be an acyclic class and
 the corresponding class of arrows in the category of
the corresponding class of arrows in the category of
chain complexes. Suppose that is
is  -presentable and
-presentable and 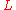 is
is  -acyclic.
-acyclic.
Then any natural transformation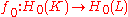
extends, in the category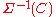 to a natural
to a natural
transformation of chain functors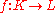 and this is
and this is
unique in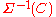 up to chain homotopies.
up to chain homotopies.
If we suppose, in addition, that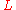 is
is  -presentable, that
-presentable, that  is
is  -acyclic, and that
-acyclic, and that 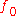 is an isomorphism, then
is an isomorphism, then  is homotopy equivalence.
is homotopy equivalence.

be the category of triangulable spaces and be the
be the
category of abelian group valued functors on . Let
. Let
 be the singular chain complex functor and
be the singular chain complex functor and 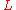
be the simplicial chain complex functor. Let be the functor that assigns to each space
be the functor that assigns to each space  the
the
space . Here,
. Here, 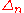 is the
is the  -simplex and this functor assigns to
-simplex and this functor assigns to  the sum of as many copies of each
the sum of as many copies of each
 -simplex as there are maps
-simplex as there are maps  .
.
Then let be defined by
be defined by 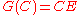 . There is an
. There is an
obvious augmentation and this induces one on
and this induces one on
 . It can be shown that both
. It can be shown that both  and
and
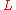 are both
are both  -presentable and
-presentable and
 -acyclic (the proof that
-acyclic (the proof that 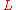 is not entirely
is not entirely
straigtforward and uses a detour through simplicial subdivision, which
can also be handled using the above theorem). The class is the class of homology equivalences. It is rather
is the class of homology equivalences. It is rather
obvious that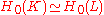 and so we conclude that
and so we conclude that
singular and simplicial homology are isomorphic on .
.
There are many other examples in both algebra and topology, some of
which are described in M. Barr, Acyclic Models. AMS, 2002.
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, a discipline within mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the acyclic models theorem can be used to show that two homology theories are isomorphic. The theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
was developed by topologists Samuel Eilenberg
Samuel Eilenberg
Samuel Eilenberg was a Polish and American mathematician of Jewish descent. He was born in Warsaw, Russian Empire and died in New York City, USA, where he had spent much of his career as a professor at Columbia University.He earned his Ph.D. from University of Warsaw in 1936. His thesis advisor...
and Saunders MacLane. They discovered that, when topologists were writing proofs to establish equivalence of various homology theories, there were numerous similarities in the processes. Eilenberg and MacLane then discovered the theorem to generalize this process.
It can be used to prove the Eilenberg–Zilber theorem
Eilenberg–Zilber theorem
In mathematics, specifically in algebraic topology, the Eilenberg–Zilber theorem is an important result in establishing the link between the homology groups of a product space X \times Y and those of the spaces X and Y. The theorem first appeared in a 1953 paper in the American Journal of...
.
Statement of the theorem
Let be an arbitrary category
be an arbitrary categoryCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
and
 be the category of chain complexes of
be the category of chain complexes of  -module
-moduleModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
s. Let
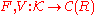 be covariant functors such that:
be covariant functors such that:
-
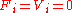 for
for  .
. - There are
 for
for  such that
such that 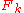 has a basis in
has a basis in 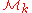 , so
, so  is a free functor.
is a free functor. -
 is
is 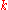 - and
- and  -acyclic at these models, which means that
-acyclic at these models, which means that 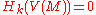 for all
for all  and all
and all  .
.
Then the following assertions hold:
- Every natural transformationNatural transformationIn category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
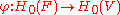 is induced by a natural chain map
is induced by a natural chain map 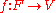 .
. - If
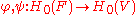 are natural transformations,
are natural transformations,  are natural chain maps as before and
are natural chain maps as before and  for all models
for all models 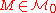 , then there is a natural chain homotopy between
, then there is a natural chain homotopy between  and
and 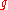 .
. - In particular the chain map
 is unique up to natural chain homotopy.
is unique up to natural chain homotopy.
Projective and acyclic complexes
What is above is one of the earliest versions of the theorem. Anotherversion is the one that says that if
 is a complex of
is a complex ofprojectives in an abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
and
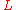 is an acyclic
is an acycliccomplex in that category, then any map
 extends to a chain map
extends to a chain map  , unique up to
, unique up tohomotopy.
This specializes almost to the above theorem if one uses the functor category
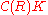 as the abelian category. Free functors are projective objects in that category. The morphisms in the functor category are natural transformations, so the constructed chain maps and homotopies are all natural. The difference is that in the above version,
as the abelian category. Free functors are projective objects in that category. The morphisms in the functor category are natural transformations, so the constructed chain maps and homotopies are all natural. The difference is that in the above version,  being acyclic is a stronger assumption than being acyclic only at certain objects.
being acyclic is a stronger assumption than being acyclic only at certain objects.On the other hand, the above version almost implies this version by letting
 a category with only one object. Then the free functor
a category with only one object. Then the free functor  is basically just free (and hence projective) module.
is basically just free (and hence projective) module.  being acyclic at the models (there is only one) means nothing else than that the complex
being acyclic at the models (there is only one) means nothing else than that the complex  is acyclic.
is acyclic.Acyclic classes
Then there is the grand theorem that unifies them all. Let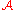 be an abelian category (for example
be an abelian category (for example  or
or 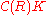 ). A class
). A class  of chain complexes over
of chain complexes over 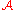 will be called an acyclic class provided:
will be called an acyclic class provided:
- The 0 complex is in
 .
. - The complex
 belongs to
belongs to  if and only if the suspension of
if and only if the suspension of  does.
does. - If the complexes
 and
and 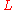 are homotopic and
are homotopic and  , then
, then 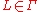 .
. - Every complex in
 is acyclic.
is acyclic. - If
 is a double complex, all of whose rows are in
is a double complex, all of whose rows are in  , then the total complex of
, then the total complex of  belongs to
belongs to  .
.
There are three natural examples of acyclic classes, although doubtless
others exist. The first is that of homotopy contractible complexes.
The second is that of acyclic complexes. In functor categories (e.g. the
category of all functors from topological spaces to abelian groups),
there is a class of complexes that are contractible on each object, but
where the contractions might not be given by natural transformations.
Another example is again in functor categories but this time the complexes are acyclic only at certain objects.
Let
 denote the class of chain maps between complexes
denote the class of chain maps between complexeswhose mapping cone belongs to
 . Although
. Although does not necessarily have a calculus of either right
does not necessarily have a calculus of either rightor left fractions, it has weaker properties of having homotopy classes
of both left and right fractions that permit forming the class
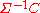 gotten by inverting the arrows in
gotten by inverting the arrows in .
.Let
 be an augmented endofunctor on
be an augmented endofunctor on  ,
,meaning there is given a natural transformation
 (the identity functor on
(the identity functor on  ). We say that the chain complex
). We say that the chain complex  is
is  -presentable if for each
-presentable if for each  , the chain
, the chaincomplex
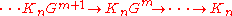
belongs to
 . The boundary operator is given by
. The boundary operator is given by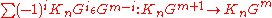 .
.We say that the chain complex functor
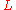 is
is -acyclic if the augmented chain complex
-acyclic if the augmented chain complex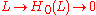 belongs to
belongs to  .
.Theorem. Let
 be an acyclic class and
be an acyclic class and the corresponding class of arrows in the category of
the corresponding class of arrows in the category ofchain complexes. Suppose that
 is
is  -presentable and
-presentable and 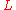 is
is  -acyclic.
-acyclic.Then any natural transformation
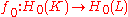
extends, in the category
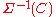 to a natural
to a naturaltransformation of chain functors
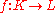 and this is
and this isunique in
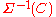 up to chain homotopies.
up to chain homotopies.If we suppose, in addition, that
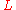 is
is  -presentable, that
-presentable, that  is
is  -acyclic, and that
-acyclic, and that 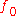 is an isomorphism, then
is an isomorphism, then  is homotopy equivalence.
is homotopy equivalence.Example
Here is an example of this last theorem in action. Let
be the category of triangulable spaces and
 be the
be thecategory of abelian group valued functors on
 . Let
. Let be the singular chain complex functor and
be the singular chain complex functor and 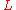
be the simplicial chain complex functor. Let
 be the functor that assigns to each space
be the functor that assigns to each space  the
thespace
 . Here,
. Here, 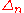 is the
is the  -simplex and this functor assigns to
-simplex and this functor assigns to  the sum of as many copies of each
the sum of as many copies of each -simplex as there are maps
-simplex as there are maps  .
.Then let
 be defined by
be defined by 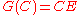 . There is an
. There is anobvious augmentation
 and this induces one on
and this induces one on . It can be shown that both
. It can be shown that both  and
and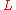 are both
are both  -presentable and
-presentable and -acyclic (the proof that
-acyclic (the proof that 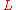 is not entirely
is not entirelystraigtforward and uses a detour through simplicial subdivision, which
can also be handled using the above theorem). The class
 is the class of homology equivalences. It is rather
is the class of homology equivalences. It is ratherobvious that
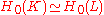 and so we conclude that
and so we conclude thatsingular and simplicial homology are isomorphic on
 .
.There are many other examples in both algebra and topology, some of
which are described in M. Barr, Acyclic Models. AMS, 2002.

