
Root test
Encyclopedia
In mathematics
, the root test is a criterion for the convergence (a convergence test) of an infinite series. It depends on the quantity
where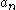 are the terms of the series, and states that the series converges absolutely if this quantity is less than unity but diverges if it is greater than unity. It is particularly useful in connection with power series.
are the terms of the series, and states that the series converges absolutely if this quantity is less than unity but diverges if it is greater than unity. It is particularly useful in connection with power series.
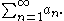
the root test uses the number
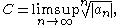
where "lim sup" denotes the limit superior, possibly ∞. Note that if
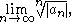
converges then it equals C and may be used in the root test instead.
The root test states that:
There are some series for which C = 1 and the series converges, e.g.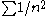 , and there are others for which C = 1 and the series diverges, e.g.
, and there are others for which C = 1 and the series diverges, e.g. 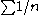 .
.
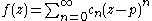
where the coefficients cn, and the center p are complex number
s and the argument z is a complex variable.
The terms of this series would then be given by an = cn(z − p)n. One then applies the root test to the an as above. Note that sometimes a series like this is called a power series "around p", because the radius of convergence is the radius R of the largest interval or disc centred at p such that the series will converge for all points z strictly in the interior (convergence on the boundary of the interval or disc generally has to be checked separately). A corollary
of the root test applied to such a power series is that the radius of convergence is exactly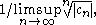 taking care that we really mean ∞ if the denominator is 0.
taking care that we really mean ∞ if the denominator is 0.
. If for all n ≥ N (N some fixed natural number
) we have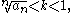 then
then 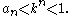 Since the geometric series
Since the geometric series 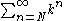 converges so does
converges so does 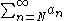 by the comparison test. Absolute convergence in case of nonpositive an can be proven in exactly the same way using
by the comparison test. Absolute convergence in case of nonpositive an can be proven in exactly the same way using 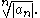
If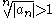 for infinitely many n, then an fails to converge to 0, hence the series is divergent.
for infinitely many n, then an fails to converge to 0, hence the series is divergent.
Proof of corollary:
For a power series Σan = Σcn(z − p)n, we see by the above that the series converges if there exists an N such that for all n ≥ N we have
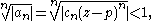
equivalent to
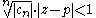
for all n ≥ N, which implies that in order for the series to converge we must have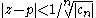 for all sufficiently large n. This is equivalent to saying
for all sufficiently large n. This is equivalent to saying
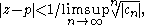
so Now the only other place where convergence is possible is when
Now the only other place where convergence is possible is when
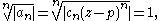
(since points > 1 will diverge) and this will not change the radius of convergence since these are just the points lying on the boundary of the interval or disc, so

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the root test is a criterion for the convergence (a convergence test) of an infinite series. It depends on the quantity

where
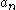 are the terms of the series, and states that the series converges absolutely if this quantity is less than unity but diverges if it is greater than unity. It is particularly useful in connection with power series.
are the terms of the series, and states that the series converges absolutely if this quantity is less than unity but diverges if it is greater than unity. It is particularly useful in connection with power series.The test
The root test was developed first by Augustin-Louis Cauchy and so is sometimes known as the Cauchy root test or Cauchy's radical test. For a series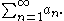
the root test uses the number
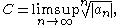
where "lim sup" denotes the limit superior, possibly ∞. Note that if
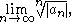
converges then it equals C and may be used in the root test instead.
The root test states that:
- if C < 1 then the series converges absolutely,
- if C > 1 then the series divergesDivergent seriesIn mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....
, - if C = 1 and the limit approaches strictly from above then the series diverges,
- otherwise the test is inconclusive (the series may diverge, converge absolutely or converge conditionally).
There are some series for which C = 1 and the series converges, e.g.
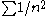 , and there are others for which C = 1 and the series diverges, e.g.
, and there are others for which C = 1 and the series diverges, e.g. 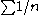 .
.Application to power series
This test can be used with a power series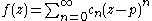
where the coefficients cn, and the center p are complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s and the argument z is a complex variable.
The terms of this series would then be given by an = cn(z − p)n. One then applies the root test to the an as above. Note that sometimes a series like this is called a power series "around p", because the radius of convergence is the radius R of the largest interval or disc centred at p such that the series will converge for all points z strictly in the interior (convergence on the boundary of the interval or disc generally has to be checked separately). A corollary
Corollary
A corollary is a statement that follows readily from a previous statement.In mathematics a corollary typically follows a theorem. The use of the term corollary, rather than proposition or theorem, is intrinsically subjective...
of the root test applied to such a power series is that the radius of convergence is exactly
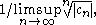 taking care that we really mean ∞ if the denominator is 0.
taking care that we really mean ∞ if the denominator is 0.Proof
The proof of the convergence of a series Σan is an application of the comparison testComparison test
In mathematics, the comparison test, sometimes called the direct comparison test or CQT is a criterion for convergence or divergence of a series whose terms are real or complex numbers...
. If for all n ≥ N (N some fixed natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
) we have
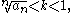 then
then 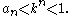 Since the geometric series
Since the geometric series 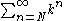 converges so does
converges so does 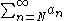 by the comparison test. Absolute convergence in case of nonpositive an can be proven in exactly the same way using
by the comparison test. Absolute convergence in case of nonpositive an can be proven in exactly the same way using 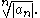
If
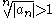 for infinitely many n, then an fails to converge to 0, hence the series is divergent.
for infinitely many n, then an fails to converge to 0, hence the series is divergent.Proof of corollary:
For a power series Σan = Σcn(z − p)n, we see by the above that the series converges if there exists an N such that for all n ≥ N we have
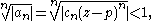
equivalent to
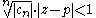
for all n ≥ N, which implies that in order for the series to converge we must have
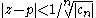 for all sufficiently large n. This is equivalent to saying
for all sufficiently large n. This is equivalent to saying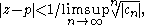
so
 Now the only other place where convergence is possible is when
Now the only other place where convergence is possible is when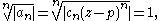
(since points > 1 will diverge) and this will not change the radius of convergence since these are just the points lying on the boundary of the interval or disc, so


