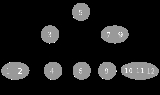
2-3-4 tree
Encyclopedia
In computer science
, a 2-3-4 tree (also called a 2-4 tree) is a self-balancing data structure
that is commonly used to implement dictionaries
. The numbers means a tree
where every node
with children (internal node) has either two children (2-node) and one data element
or three children (3-node) and two data elements or four children (4-node) and three data elements.
2-3-4 trees are B-tree
s of order 4; like B-trees in general, they can search, insert and delete in O(log n) time. One property of a 2-3-4 tree is that all external nodes are at the same
depth.
2-3-4 trees are an isometry
of red-black trees, meaning that they are equivalent data structures. In other words, for every 2-3-4 tree, there exists at least one red-black tree with data elements in the same order. Moreover, insertion and deletion operations on 2-3-4 trees that cause node expansions, splits and merges are equivalent to the color-flipping and rotations in red-black trees. Introductions to red-black trees usually introduce 2-3-4 trees first, because they are conceptually simpler. 2-3-4 trees, however, can be difficult to implement in most programming languages because of the large number of special cases involved in operations on the tree. Red-black tree
s are simpler to implement, so tend to be used instead.
Find the element to be deleted. If the element is not in a leaf node remember its location and continue searching until a leaf, which will contain the element’s successor, is reached. Then swap the leaf element with the one to be deleted, and delete the element node. It is simplest to make adjustments to the tree from the top down, as the element to be deleted is pursued that guarantee that the leaf node found is not a two-node, so that we can delete something from it and leave it there.
The adjustments we make on the way to a leaf are as follows:
Assume, without loss of generality, that the child we are about to go to is the leftmost.
If we're at the root
If the root and both children are two-nodes, combine all three elements into the root, making a 4-node and shortening the tree,
Otherwise, if the root and left child are two-nodes, the right child isn't a two-node. Perform a left rotation to make the left sibling a 3-node, and move
to the left child.
From now on, we can be sure that we're at a node which is not a 2-node.
If the leftmost child is not a 2-node, just move to it.
If the adjacent sibling is not a 2-node, perform a left rotation using its leftmost element to make the left child a 3-node.
Otherwise, add the leftmost element of the parent and the single element of the sibling to the left node, making it a 4-node, and discard the empty sibling.
Go to the left-most child.
Deletion in a 2-3-4 tree is O(log n), assuming transfer and fusion run in constant time ( O(1) ).
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, a 2-3-4 tree (also called a 2-4 tree) is a self-balancing data structure
Data structure
In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...
that is commonly used to implement dictionaries
Associative array
In computer science, an associative array is an abstract data type composed of a collection of pairs, such that each possible key appears at most once in the collection....
. The numbers means a tree
Tree (data structure)
In computer science, a tree is a widely-used data structure that emulates a hierarchical tree structure with a set of linked nodes.Mathematically, it is an ordered directed tree, more specifically an arborescence: an acyclic connected graph where each node has zero or more children nodes and at...
where every node
Node (computer science)
A node is a record consisting of one or more fields that are links to other nodes, and a data field. The link and data fields are often implemented by pointers or references although it is also quite common for the data to be embedded directly in the node. Nodes are used to build linked, often...
with children (internal node) has either two children (2-node) and one data element
Data element
In metadata, the term data element is an atomic unit of data that has precise meaning or precise semantics. A data element has:# An identification such as a data element name# A clear data element definition# One or more representation terms...
or three children (3-node) and two data elements or four children (4-node) and three data elements.
2-3-4 trees are B-tree
B-tree
In computer science, a B-tree is a tree data structure that keeps data sorted and allows searches, sequential access, insertions, and deletions in logarithmic time. The B-tree is a generalization of a binary search tree in that a node can have more than two children...
s of order 4; like B-trees in general, they can search, insert and delete in O(log n) time. One property of a 2-3-4 tree is that all external nodes are at the same
depth.
2-3-4 trees are an isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of red-black trees, meaning that they are equivalent data structures. In other words, for every 2-3-4 tree, there exists at least one red-black tree with data elements in the same order. Moreover, insertion and deletion operations on 2-3-4 trees that cause node expansions, splits and merges are equivalent to the color-flipping and rotations in red-black trees. Introductions to red-black trees usually introduce 2-3-4 trees first, because they are conceptually simpler. 2-3-4 trees, however, can be difficult to implement in most programming languages because of the large number of special cases involved in operations on the tree. Red-black tree
Red-black tree
A red–black tree is a type of self-balancing binary search tree, a data structure used in computer science, typically to implement associative arrays. The original structure was invented in 1972 by Rudolf Bayer and named "symmetric binary B-tree," but acquired its modern name in a paper in 1978 by...
s are simpler to implement, so tend to be used instead.
Properties
- Every non-leaf is a 2-node, 3-node or a 4-node. A 2-node contains one data item and has two children. A 3-node contains two data items and has 3 children. A 4-node contains 3 data items and has 4 children.
- All leaves are at the same level (the bottom level)
- All data are kept in sorted order
- Every non-leaf node will contain 1, 2 or 3 fields.
Insertion
To insert a value, we start at the root of the 2-3-4 tree:- If the current node is a 4-node:
- Remove and save the middle value to get a 3-node.
- Split the remaining 3-node up into a pair of 2-nodes (the now missing middle value is handled in the next step).
- If this is the root node (which thus has no parent):
- the middle value becomes the new root 2-node and the tree height increases by 1. Ascend into the root.
- Otherwise, push the middle value up into the parent node. Ascend into the parent node.
- Find the child whose interval contains the value to be inserted.
- If that child is a leaf, insert the value into current node and finish.
- Otherwise, descend into the child and repeat from step 1.
Example
To insert the value "25" into this 2-3-4 tree:-
- Begin at the root (10, 20) and descend towards the rightmost child (22, 24, 29). (Its interval (20, ∞) contains 25.)
- Node (22, 24, 29) is a 4-node, so its middle element 24 is pushed up into the parent node.
-
- The remaining 3-node (22, 29) is split into a pair of 2-nodes (22) and (29). Ascend back into the new parent (10, 20, 24).
- Descend towards the rightmost child (29). (Its interval (24, ∞) contains 25.)
-
- Node (29) has no leftmost child. (The child for interval (∞, 29) is empty.) Stop here and insert value 25 into this node.
Deletion
Consider just leaving the element there, marking it “deleted,” possibly to re-used for a future insertion.Find the element to be deleted. If the element is not in a leaf node remember its location and continue searching until a leaf, which will contain the element’s successor, is reached. Then swap the leaf element with the one to be deleted, and delete the element node. It is simplest to make adjustments to the tree from the top down, as the element to be deleted is pursued that guarantee that the leaf node found is not a two-node, so that we can delete something from it and leave it there.
The adjustments we make on the way to a leaf are as follows:
Assume, without loss of generality, that the child we are about to go to is the leftmost.
If we're at the root
If the root and both children are two-nodes, combine all three elements into the root, making a 4-node and shortening the tree,
Otherwise, if the root and left child are two-nodes, the right child isn't a two-node. Perform a left rotation to make the left sibling a 3-node, and move
to the left child.
From now on, we can be sure that we're at a node which is not a 2-node.
If the leftmost child is not a 2-node, just move to it.
If the adjacent sibling is not a 2-node, perform a left rotation using its leftmost element to make the left child a 3-node.
Otherwise, add the leftmost element of the parent and the single element of the sibling to the left node, making it a 4-node, and discard the empty sibling.
Go to the left-most child.
Deletion in a 2-3-4 tree is O(log n), assuming transfer and fusion run in constant time ( O(1) ).

