
Zero dagger
Encyclopedia
In set theory
, 0† (zero dagger) is a particular subset of the natural numbers, first defined by Robert M. Solovay
in unpublished work in the 1960s. (The superscript † should be a dagger, but it appears as a plus sign on some browsers.) The definition is a bit awkward, because there might be no set of natural numbers satisfying the conditions. Specifically, if ZFC is consistent
, then ZFC + "0† does not exist" is consistent. ZFC + "0† exists" is not known to be inconsistent (and most set theorists believe that it is consistent). In other words, it is believed to be independent (see large cardinal
for a discussion). It is usually formulated as follows:
If 0† exists, then a careful analysis of the embeddings of L[U] into itself reveals that there is a closed unbounded subset of κ, and a closed unbounded proper class of ordinals greater than κ, which together are indiscernible
for the structure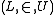 , and 0† is defined to be the set of Gödel number
, and 0† is defined to be the set of Gödel number
s of the true formulas about the indiscernibles in L[U].
Solovay showed that the existence of 0† follows from the existence of two measurable cardinals. It is traditionally considered a large cardinal axiom, although it is not a large cardinal, nor indeed a cardinal at all.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, 0† (zero dagger) is a particular subset of the natural numbers, first defined by Robert M. Solovay
Robert M. Solovay
Robert Martin Solovay is an American mathematician specializing in set theory.Solovay earned his Ph.D. from the University of Chicago in 1964 under the direction of Saunders Mac Lane, with a dissertation on A Functorial Form of the Differentiable Riemann–Roch theorem...
in unpublished work in the 1960s. (The superscript † should be a dagger, but it appears as a plus sign on some browsers.) The definition is a bit awkward, because there might be no set of natural numbers satisfying the conditions. Specifically, if ZFC is consistent
Consistency
Consistency can refer to:* Consistency , the psychological need to be consistent with prior acts and statements* "Consistency", an 1887 speech by Mark Twain...
, then ZFC + "0† does not exist" is consistent. ZFC + "0† exists" is not known to be inconsistent (and most set theorists believe that it is consistent). In other words, it is believed to be independent (see large cardinal
Large cardinal property
In the mathematical field of set theory, a large cardinal property is a certain kind of property of transfinite cardinal numbers. Cardinals with such properties are, as the name suggests, generally very "large"...
for a discussion). It is usually formulated as follows:
- 0† exists if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
there exists a non-trivial elementary embedding j : L[U] → L[U] for the relativized Gödel constructible universe L[U], where U is an ultrafilterUltrafilterIn the mathematical field of set theory, an ultrafilter on a set X is a collection of subsets of X that is a filter, that cannot be enlarged . An ultrafilter may be considered as a finitely additive measure. Then every subset of X is either considered "almost everything" or "almost nothing"...
witnessing that some cardinal κ is measurableMeasurable cardinal- Measurable :Formally, a measurable cardinal is an uncountable cardinal number κ such that there exists a κ-additive, non-trivial, 0-1-valued measure on the power set of κ...
.
If 0† exists, then a careful analysis of the embeddings of L[U] into itself reveals that there is a closed unbounded subset of κ, and a closed unbounded proper class of ordinals greater than κ, which together are indiscernible
Indiscernibles
In mathematical logic, indiscernibles are objects which cannot be distinguished by any property or relation defined by a formula. Usually only first-order formulas are considered...
for the structure
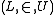 , and 0† is defined to be the set of Gödel number
, and 0† is defined to be the set of Gödel numberGödel number
In mathematical logic, a Gödel numbering is a function that assigns to each symbol and well-formed formula of some formal language a unique natural number, called its Gödel number. The concept was famously used by Kurt Gödel for the proof of his incompleteness theorems...
s of the true formulas about the indiscernibles in L[U].
Solovay showed that the existence of 0† follows from the existence of two measurable cardinals. It is traditionally considered a large cardinal axiom, although it is not a large cardinal, nor indeed a cardinal at all.
See also
- 0#Zero sharpIn the mathematical discipline of set theory, 0# is the set of true formulas about indiscernibles in the Gödel constructible universe. It is often encoded as a subset of the integers , or as a subset of the hereditarily finite sets, or as a real number...
: a set of formulas (or subset of the integers) defined in a similar fashion, but simpler.

