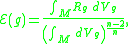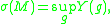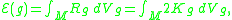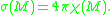Yamabe invariant
Encyclopedia
In mathematics
, in the field of differential geometry, the Yamabe invariant (also referred to as the sigma constant) is a real number invariant associated to a smooth manifold that is preserved under diffeomorphisms. It was first written down independently by O. Kobayashi and R. Schoen
and takes its name from H. Yamabe
.
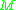be a compact
smooth manifold of dimension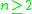
. The normalized Einstein–Hilbert functional 
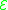assigns to each Riemannian metric 
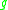on 
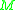a real number as follows:
where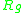
is the scalar curvature
of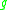
and 
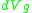is the volume form
associated to the metric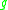
. Note that the exponent in the denominator is chosen so that the functional is scale-invariant. We may think of 
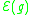as measuring the average scalar curvature of 
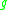over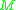 
. It was conjectured by Yamabe that every conformal class
of metrics contains a metric of constant scalar curvature (the so-called Yamabe problem
); it was proven by Yamabe, Trudinger
, Aubin
, and Schoen that a minimum value of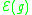
is attained in each conformal class of metrics, and in particular this minimum is achieved by a metric of constant scalar curvature. We may thus define
where the infimum is taken over the smooth functions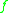
on 
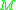. The number 
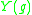is sometimes called the conformal
Yamabe energy of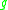
(and is constant on conformal classes).
A comparison argument due to Aubin shows that for any metric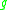
, 
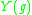is bounded above by 
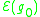, where
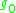is the standard metric on the 
-sphere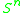 
. The number 
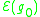is equal
to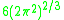
and is often denoted 
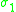. It follows that if we define
where the supremum is taken over all metrics on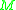
, then 
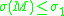(and is in particular finite). The
real number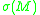
is called the Yamabe invariant of 
.
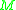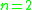, (so that M is a closed surface) the Einstein–Hilbert functional is given by
where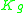
is the Gauss curvature of g. However, by the Gauss–Bonnet theorem
, the integral of the Gauss curvature is given by
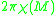, where 
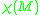is the Euler characteristic
of M. In particular, this number does not depend on the choice of metric. Therefore, for surfaces, we conclude that
For example, the 2-sphere has Yamabe invariant equal to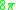
, and the 2-torus has Yamabe invariant equal to zero.
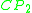is realized by the Fubini–Study metric, and so is less than that of the 4-sphere. Most of these arguments involve Seiberg–Witten theory, and so are specific
to dimension 4.
An important result due to Petean states that if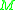
is simply connected and has dimension 
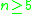, then 
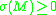. In light of Perelman's solution of the Poincaré conjecture
, it follows that a simply connected
-manifold can have negative Yamabe invariant only if 
. On the other hand, as has already been indicated, simply connected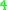 
-manifolds do in fact often have negative Yamabe invariants.
Below is a table of some smooth manifolds of dimension three with known Yamabe invariant. Recall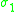
is defined above to
be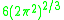
.
By an argument due to Anderson, Perelman's results on the Ricci flow
imply that the constant-curvature metric on any hyperbolic 3-manifold realizes the Yamabe invariant. This provides us with infinitely many examples
of 3-manifolds for which the invariant is both negative and
exactly computable.
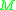holds important topological information. For example, 
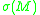is positive
if and only if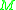
admits a metric of positive scalar curvature. The significance of this fact is that much is known about the topology of manifolds with metrics of positive scalar curvature.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the field of differential geometry, the Yamabe invariant (also referred to as the sigma constant) is a real number invariant associated to a smooth manifold that is preserved under diffeomorphisms. It was first written down independently by O. Kobayashi and R. Schoen
Richard Schoen
Richard Melvin Schoen is an American mathematician. Born in Fort Recovery, Ohio, he received his PhD in 1977 from Stanford University where he is currently the Anne T. and Robert M. Bass Professor of Humanities and Sciences...
and takes its name from H. Yamabe
Hidehiko Yamabe
-External links:...
.
Definition
Let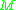 be a compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
smooth manifold of dimension
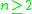. The normalized Einstein–Hilbert functional assigns to each Riemannian metric on 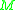a real number as follows:
where
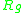is the scalar curvatureScalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
of
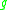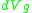and is the volume formVolume form
In mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
associated to the metric
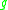. Note that the exponent in the denominator is chosen so that the functional is scale-invariant. We may think of 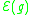as measuring the average scalar curvature of 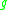over 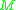. It was conjectured by Yamabe that every conformal classConformal map
In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
of metrics contains a metric of constant scalar curvature (the so-called Yamabe problem
Yamabe problem
The Yamabe problem in differential geometry concerns the existence of Riemannian metrics with constant scalar curvature, and takes its name from the mathematician Hidehiko Yamabe. Although claimed to have a solution in 1960, a critical error...
); it was proven by Yamabe, Trudinger
Neil Trudinger
Neil Sidney Trudinger is an Australian mathematician, known particularly for his work in the field of nonlinear elliptic partial differential equations....
, Aubin
Thierry Aubin
Thierry Aubin was a French mathematician at Centre de Mathématiques de Jussieu who worked on Riemannian geometryand non-linear partial differential equations...
, and Schoen that a minimum value of
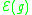is attained in each conformal class of metrics, and in particular this minimum is achieved by a metric of constant scalar curvature. We may thus define
where the infimum is taken over the smooth functions
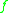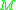on . The number 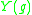is sometimes called the conformalYamabe energy of
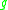(and is constant on conformal classes).A comparison argument due to Aubin shows that for any metric
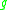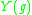, is bounded above by 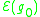, where 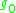is the standard metric on the -sphere 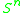. The number 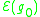is equalto
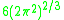and is often denoted 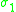. It follows that if we define
where the supremum is taken over all metrics on
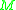, then 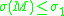(and is in particular finite). Thereal number
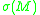is called the Yamabe invariant of 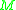.The Yamabe invariant in two dimensions
In the case that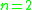, (so that M is a closed surface) the Einstein–Hilbert functional is given by
where
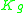is the Gauss curvature of g. However, by the Gauss–Bonnet theoremGauss–Bonnet theorem
The Gauss–Bonnet theorem or Gauss–Bonnet formula in differential geometry is an important statement about surfaces which connects their geometry to their topology...
, the integral of the Gauss curvature is given by
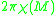, where 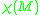is the Euler characteristicEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of M. In particular, this number does not depend on the choice of metric. Therefore, for surfaces, we conclude that
For example, the 2-sphere has Yamabe invariant equal to
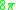, and the 2-torus has Yamabe invariant equal to zero.Examples
In the late 1990s, the Yamabe invariant was computed for large classes of 4-manifolds by LeBrun and his collaborators. In particular, it was shown that most compact complex surfaces have negative, exactly computable Yamabe invariant, and that any Kahler–Einstein metric of negative scalar curvature realizes the Yamabe invariant in dimension 4. It was also shown that the Yamabe invariant of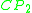 is realized by the Fubini–Study metric, and so is less than that of the 4-sphere. Most of these arguments involve Seiberg–Witten theory, and so are specificto dimension 4.
An important result due to Petean states that if
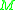is simply connected and has dimension 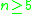, then 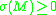. In light of Perelman's solution of the Poincaré conjecturePoincaré conjecture
In mathematics, the Poincaré conjecture is a theorem about the characterization of the three-dimensional sphere , which is the hypersphere that bounds the unit ball in four-dimensional space...
, it follows that a simply connected
-manifold can have negative Yamabe invariant only if . On the other hand, as has already been indicated, simply connected 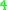-manifolds do in fact often have negative Yamabe invariants.Below is a table of some smooth manifolds of dimension three with known Yamabe invariant. Recall
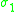is defined above tobe
.  |
 |
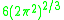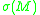notes |
|---|---|---|
 Sphere A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point... |
 |
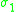the 3-sphere Sphere A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point... |
 |
 |
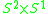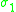the trivial 2-sphere bundle over  |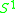
 |
 |
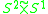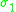the unique non-orientable 2-sphere bundle over  |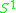
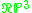 Real projective space In mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:... |
 |
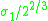computed by Bray and Neves |
 |
 |
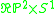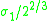computed by Bray and Neves |
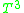 Torus In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle... |
 |
the 3-torus Torus In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle... |
By an argument due to Anderson, Perelman's results on the Ricci flow
Ricci flow
In differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric....
imply that the constant-curvature metric on any hyperbolic 3-manifold realizes the Yamabe invariant. This provides us with infinitely many examples
of 3-manifolds for which the invariant is both negative and
exactly computable.
Topological significance
The sign of the Yamabe invariant of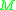 holds important topological information. For example, 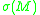is positiveif and only if
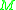admits a metric of positive scalar curvature. The significance of this fact is that much is known about the topology of manifolds with metrics of positive scalar curvature.