
Tarski–Seidenberg theorem
Encyclopedia
In mathematics
, the Tarski–Seidenberg theorem states that a set in (n + 1)-dimensional space defined by polynomial identities and inequalities can be projected down onto n-dimensional space, and the resulting set is still definable in terms of polynomial identities and inequalities. The theorem — also known as the Tarski–Seidenberg projection property — is named after Alfred Tarski
and Abraham Seidenberg
.
in Rn is a finite union of sets defined by a finite number of polynomial equations and inequalities, that is by a finite number of statements of the form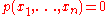
and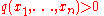
for polynomials p and q. We define a projection map π : Rn+1 → Rn by sending a point (x1,...,xn,xn+1) to (x1,...,xn). Then the Tarski-Seidenberg theorem states that if X is a semialgebraic set in Rn+1 for some n > 1, then π(X) is a semialgebraic set in Rn.
s rather than semialgebraic sets. For these sets the theorem fails. As a simple example consider the circle in R2 defined by the equation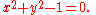
This is a perfectly good algebraic set, but project it down by sending (x,y) in R2 to x in R and we have the set of points satisfying -1 ≤ x ≤ 1. This is a semialgebraic set as we would expect from the theorem, but it is not an algebraic set.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Tarski–Seidenberg theorem states that a set in (n + 1)-dimensional space defined by polynomial identities and inequalities can be projected down onto n-dimensional space, and the resulting set is still definable in terms of polynomial identities and inequalities. The theorem — also known as the Tarski–Seidenberg projection property — is named after Alfred Tarski
Alfred Tarski
Alfred Tarski was a Polish logician and mathematician. Educated at the University of Warsaw and a member of the Lwow-Warsaw School of Logic and the Warsaw School of Mathematics and philosophy, he emigrated to the USA in 1939, and taught and carried out research in mathematics at the University of...
and Abraham Seidenberg
Abraham Seidenberg
Abraham Seidenberg was an American mathematician.- Early life :Seidenberg was born on June 2, 1916 in Washington D.C.. He graduated with a B.A. from the University of Maryland in 1937. He completed his Ph.D. in mathematics from Johns Hopkins University in 1943. His Ph.D...
.
Statement
A semialgebraic setSemialgebraic set
In mathematics, a semialgebraic set is a subset S of Rn for some real closed field R defined by a finite sequence of polynomial equations and inequalities , or any finite union of such sets. A semialgebraic function is a function with semialgebraic graph...
in Rn is a finite union of sets defined by a finite number of polynomial equations and inequalities, that is by a finite number of statements of the form
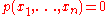
and
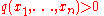
for polynomials p and q. We define a projection map π : Rn+1 → Rn by sending a point (x1,...,xn,xn+1) to (x1,...,xn). Then the Tarski-Seidenberg theorem states that if X is a semialgebraic set in Rn+1 for some n > 1, then π(X) is a semialgebraic set in Rn.
Failure with algebraic sets
If we only define sets using polynomial equations and not inequalities then we define algebraic setAlgebraic set
In mathematics, an algebraic set over an algebraically closed field K is the set of solutions in Kn of a set of simultaneous equationsand so on up to...
s rather than semialgebraic sets. For these sets the theorem fails. As a simple example consider the circle in R2 defined by the equation
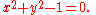
This is a perfectly good algebraic set, but project it down by sending (x,y) in R2 to x in R and we have the set of points satisfying -1 ≤ x ≤ 1. This is a semialgebraic set as we would expect from the theorem, but it is not an algebraic set.

