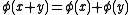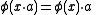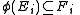Supermodule
Encyclopedia
In mathematics
, a supermodule is a Z2-graded module over a superring or superalgebra
. Supermodules arise in super linear algebra which is a mathematical framework for studying the concept supersymmetry
in theoretical physics
.
Supermodules over a commutative superalgebra can be viewed as generalizations of super vector space
s over a (purely even) field
K. Supermodules often play a more prominent role in super linear algebra than do super vector spaces. These reason is that it is often necessary or useful to extend the field of scalars to include odd variables. In doing so one moves from fields to commutative superalgebras and from vector spaces to modules.
. A right supermodule over A is a right module E over A with a direct sum
decomposition (as an abelian group
)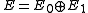
such that multiplication by elements of A satisfies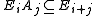
for all i and j in Z2. The subgroups Ei are then right A0-modules.
The elements of Ei are said to be homogeneous. The parity of a homogeneous element x, denoted by |x|, is 0 or 1 according to whether it is in E0 or E1. Elements of parity 0 are said to be even and those of parity 1 to be odd. If a is a homogeneous scalar and x is a homogeneous element of E then |x·a| is homogeneous and |x·a| = |x| + |a|.
Likewise, left supermodules and superbimodules are defined as left modules or bimodule
s over A whose scalar multiplications respect the gradings in the obvious manner. If A is supercommutative, then every left or right supermodule over A may be regarded as a superbimodule by setting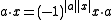
for homogeneous elements a ∈ A and x ∈ E, and extending by linearity. If A is purely even this reduces to the ordinary definition.
between supermodules is a module homomorphism that preserves the grading.
Let E and F be right supermodules over A. A map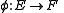
is a supermodule homomorphism if
for all a∈A and all x,y∈E. The set of all module homomorphisms from E to F is denoted by Hom(E, F).
In many cases, it is necessary or convenient to consider a larger class of morphisms between supermodules. Let A be a supercommutative algebra. Then all supermodules over A be regarded as superbimodules in a natural fashion. For supermodules E and F, let Hom(E, F) denote the space of all right A-linear maps (i.e. all module homomorphisms from E to F considered as ungraded right A-modules). There is a natural grading on Hom(E, F) where the even homomorphisms are those that preserve the grading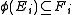
and the odd homomorphisms are those that reverse the grading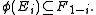
If φ is homogeneous then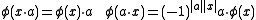
where x and a are homogeneous elements of E and A respectively. The even homomorphisms are both right and left linear whereas the odd homomorphism are right linear but left antilinear (with respect to the grading automorphism).
The set Hom(E, F) can be given the structure of a bimodule over A by setting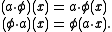
With the above grading Hom(E, F) becomes a supermodule over A whose even part is the set of all ordinary supermodule homomorphisms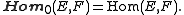
In the language of category theory
, the class of all supermodules over A forms a category
with supermodule homomorphisms as the morphisms. This category is a symmetric monoidal closed category under the super tensor product whose internal Hom functor is given by Hom.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a supermodule is a Z2-graded module over a superring or superalgebra
Superalgebra
In mathematics and theoretical physics, a superalgebra is a Z2-graded algebra. That is, it is an algebra over a commutative ring or field with a decomposition into "even" and "odd" pieces and a multiplication operator that respects the grading....
. Supermodules arise in super linear algebra which is a mathematical framework for studying the concept supersymmetry
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
in theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
.
Supermodules over a commutative superalgebra can be viewed as generalizations of super vector space
Super vector space
In mathematics, a super vector space is another name for a Z2-graded vector space, that is, a vector space over a field K with a given decompositionV=V_0\oplus V_1....
s over a (purely even) field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K. Supermodules often play a more prominent role in super linear algebra than do super vector spaces. These reason is that it is often necessary or useful to extend the field of scalars to include odd variables. In doing so one moves from fields to commutative superalgebras and from vector spaces to modules.
- In this article, all superalgebras are assumed be associative and unital unless stated otherwise.
Formal definition
Let A be a fixed superalgebraSuperalgebra
In mathematics and theoretical physics, a superalgebra is a Z2-graded algebra. That is, it is an algebra over a commutative ring or field with a decomposition into "even" and "odd" pieces and a multiplication operator that respects the grading....
. A right supermodule over A is a right module E over A with a direct sum
Direct sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
decomposition (as an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
)
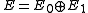
such that multiplication by elements of A satisfies
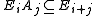
for all i and j in Z2. The subgroups Ei are then right A0-modules.
The elements of Ei are said to be homogeneous. The parity of a homogeneous element x, denoted by |x|, is 0 or 1 according to whether it is in E0 or E1. Elements of parity 0 are said to be even and those of parity 1 to be odd. If a is a homogeneous scalar and x is a homogeneous element of E then |x·a| is homogeneous and |x·a| = |x| + |a|.
Likewise, left supermodules and superbimodules are defined as left modules or bimodule
Bimodule
In abstract algebra a bimodule is an abelian group that is both a left and a right module, such that the left and right multiplications are compatible...
s over A whose scalar multiplications respect the gradings in the obvious manner. If A is supercommutative, then every left or right supermodule over A may be regarded as a superbimodule by setting
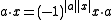
for homogeneous elements a ∈ A and x ∈ E, and extending by linearity. If A is purely even this reduces to the ordinary definition.
Homomorphisms
A homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
between supermodules is a module homomorphism that preserves the grading.
Let E and F be right supermodules over A. A map
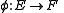
is a supermodule homomorphism if
for all a∈A and all x,y∈E. The set of all module homomorphisms from E to F is denoted by Hom(E, F).
In many cases, it is necessary or convenient to consider a larger class of morphisms between supermodules. Let A be a supercommutative algebra. Then all supermodules over A be regarded as superbimodules in a natural fashion. For supermodules E and F, let Hom(E, F) denote the space of all right A-linear maps (i.e. all module homomorphisms from E to F considered as ungraded right A-modules). There is a natural grading on Hom(E, F) where the even homomorphisms are those that preserve the grading
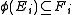
and the odd homomorphisms are those that reverse the grading
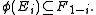
If φ is homogeneous then
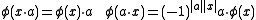
where x and a are homogeneous elements of E and A respectively. The even homomorphisms are both right and left linear whereas the odd homomorphism are right linear but left antilinear (with respect to the grading automorphism).
The set Hom(E, F) can be given the structure of a bimodule over A by setting
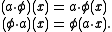
With the above grading Hom(E, F) becomes a supermodule over A whose even part is the set of all ordinary supermodule homomorphisms
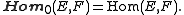
In the language of category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, the class of all supermodules over A forms a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
with supermodule homomorphisms as the morphisms. This category is a symmetric monoidal closed category under the super tensor product whose internal Hom functor is given by Hom.