
Størmer's theorem
Encyclopedia
In number theory
, Størmer's theorem, named after Carl Størmer
, gives a finite bound on the number of consecutive pairs of smooth numbers that exist, for a given degree of smoothness, and provides a method for finding all such pairs using Pell equations. It follows from the Thue–Siegel–Roth theorem
that there are only a finite number of pairs of this type, but Størmer gave a procedure for finding them all.
Louis Mordell
wrote about this result, saying that it "is very pretty, and there are many applications of it."
, musical tones can be described as integer multiples of a fundamental frequency
, and the multiples generated by products of small prime numbers are of particular importance: in Pythagorean tuning
, only tones corresponding to integer multiples of the form 2i × 3j are allowed, while in just tuning, only the tones corresponding to numbers of the form 2i × 3j × 5k are allowed, where i, j, and k may range over any non-negative integer value. The difference between one tone and another forms a musical interval
that can be measured by the ratio
between the two corresponding integers, and in music the superparticular ratios between consecutive integers are of particular importance.
Størmer's theorem implies that, for Pythagorean tuning, the only possible superparticular ratios are 2/1 (the octave
), 3/2 (the perfect fifth
), 4/3 (the perfect fourth
), and 9/8 (the whole step). That is, the only pairs of consecutive integers that have only powers of two and three in their prime factorizations are (1,2), (2,3), (3,4), and (8,9). For just tuning, six additional superparticular ratios are available: 5/4, 6/5, 10/9, 16/15, 25/24, and 81/80; all are musically meaningful.
Some modern musical theorists have developed p-limit
musical tuning systems for primes p larger than 5; Størmer's theorem applies as well in these cases, and describes how to calculate the set of possible superparticular ratios for these systems.
s and considers the set of integers
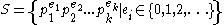
that can be generated by products of numbers in P, then there are only finitely many pairs of consecutive numbers in S. Further, it gives a method of finding them all using Pell equations.
Let P be the given set of primes, and define a number to be P-smooth
if all its prime factors belong to P. Assume p1 = 2; otherwise there can be no consecutive P-smooth numbers. Lehmer's method involves solving the Pell equation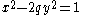
for each P-smooth square-free number q other than 2. Each such number q is generated as a product of a subset of P, so there are 2k-1 Pell equations to solve. For each such equation, let xi,yi be the generated solutions, for i in the range [1,max(3,(pk+1)/2)], where pk is the largest of the primes in P.
Then, as Lehmer shows, all consecutive pairs of P-smooth numbers are of the form (xi - 1)/2, (xi + 1)/2. Thus one can find all such pairs by testing the numbers of this form for P-smoothness.
giving the superparticular ratios for just tuning, let P = {2,3,5}. There are seven P-smooth squarefree numbers q (omitting the eighth P-smooth squarefree number, 2): 1, 3, 5, 6, 10, 15, and 30, each of which leads to a Pell equation. The number of solutions per Pell equation required by Lehmer's method is max(3,(5+1)/2) = 3, so this method generates three solutions to each Pell equation, as follows.
The number of consecutive pairs of integers that are smooth with respect to the first k primes are
The largest integer from all these pairs, for each k, is
OEIS also lists the number of pairs of this type where the larger of the two integers in the pair is square or triangular
, as both types of pair arise frequently.
.
Mabkhout (1993) proved that every number x4 + 1, for x > 3, has a prime factor greater than or equal to 137. Størmer's theorem is an important part of his proof, in which he reduces the problem to the solution of 128 Pell equations.
Several authors have extended Størmer's work by providing methods for listing the solutions to more general diophantine equation
s, or by providing more general divisibility criteria for the solutions to Pell equations.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, Størmer's theorem, named after Carl Størmer
Carl Størmer
Fredrik Carl Mülertz Størmer was a Norwegian mathematician and physicist, known both for his work in number theory and for studying the movement of charged particles in the magnetosphere and the formation of aurorae....
, gives a finite bound on the number of consecutive pairs of smooth numbers that exist, for a given degree of smoothness, and provides a method for finding all such pairs using Pell equations. It follows from the Thue–Siegel–Roth theorem
Thue–Siegel–Roth theorem
In mathematics, the Thue–Siegel–Roth theorem, also known simply as Roth's theorem, is a foundational result in diophantine approximation to algebraic numbers. It is of a qualitative type, stating that a given algebraic number α may not have too many rational number approximations, that are 'very...
that there are only a finite number of pairs of this type, but Størmer gave a procedure for finding them all.
Louis Mordell
Louis Mordell
Louis Joel Mordell was a British mathematician, known for pioneering research in number theory. He was born in Philadelphia, USA, in a Jewish family of Lithuanian extraction...
wrote about this result, saying that it "is very pretty, and there are many applications of it."
Application in music theory
In the theory of musical tuningMusical tuning
In music, there are two common meanings for tuning:* Tuning practice, the act of tuning an instrument or voice.* Tuning systems, the various systems of pitches used to tune an instrument, and their theoretical bases.-Tuning practice:...
, musical tones can be described as integer multiples of a fundamental frequency
Fundamental frequency
The fundamental frequency, often referred to simply as the fundamental and abbreviated f0, is defined as the lowest frequency of a periodic waveform. In terms of a superposition of sinusoids The fundamental frequency, often referred to simply as the fundamental and abbreviated f0, is defined as the...
, and the multiples generated by products of small prime numbers are of particular importance: in Pythagorean tuning
Pythagorean tuning
Pythagorean tuning is a system of musical tuning in which the frequency relationships of all intervals are based on the ratio 3:2. This interval is chosen because it is one of the most consonant...
, only tones corresponding to integer multiples of the form 2i × 3j are allowed, while in just tuning, only the tones corresponding to numbers of the form 2i × 3j × 5k are allowed, where i, j, and k may range over any non-negative integer value. The difference between one tone and another forms a musical interval
Interval (music)
In music theory, an interval is a combination of two notes, or the ratio between their frequencies. Two-note combinations are also called dyads...
that can be measured by the ratio
Ratio
In mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
between the two corresponding integers, and in music the superparticular ratios between consecutive integers are of particular importance.
Størmer's theorem implies that, for Pythagorean tuning, the only possible superparticular ratios are 2/1 (the octave
Octave
In music, an octave is the interval between one musical pitch and another with half or double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems"...
), 3/2 (the perfect fifth
Perfect fifth
In classical music from Western culture, a fifth is a musical interval encompassing five staff positions , and the perfect fifth is a fifth spanning seven semitones, or in meantone, four diatonic semitones and three chromatic semitones...
), 4/3 (the perfect fourth
Perfect fourth
In classical music from Western culture, a fourth is a musical interval encompassing four staff positions , and the perfect fourth is a fourth spanning five semitones. For example, the ascending interval from C to the next F is a perfect fourth, as the note F lies five semitones above C, and there...
), and 9/8 (the whole step). That is, the only pairs of consecutive integers that have only powers of two and three in their prime factorizations are (1,2), (2,3), (3,4), and (8,9). For just tuning, six additional superparticular ratios are available: 5/4, 6/5, 10/9, 16/15, 25/24, and 81/80; all are musically meaningful.
Some modern musical theorists have developed p-limit
Limit (music)
In music theory, limit or harmonic limit is a way of characterizing the harmony found in a piece or genre of music, or the harmonies that can be made using a particular scale. The term was introduced by Harry Partch, who used it to give an upper bound on the complexity of harmony; hence the name...
musical tuning systems for primes p larger than 5; Størmer's theorem applies as well in these cases, and describes how to calculate the set of possible superparticular ratios for these systems.
Formal statement of the theorem
Formally, the theorem states that, if one chooses a finite set P = {p1, ... pk} of prime numberPrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s and considers the set of integers
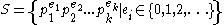
that can be generated by products of numbers in P, then there are only finitely many pairs of consecutive numbers in S. Further, it gives a method of finding them all using Pell equations.
The procedure
Størmer's original procedure involves solving a set of roughly 3k Pell equations, in each one finding only the smallest solution. A simplified version of the procedure, due to D. H. Lehmer, is described below; it solves fewer equations but finds more solutions in each equation.Let P be the given set of primes, and define a number to be P-smooth
Smooth number
In number theory, a smooth number is an integer which factors completely into small prime numbers. The term seems to have been coined by Leonard Adleman. Smooth numbers are especially important in cryptography relying on factorization.-Definition:...
if all its prime factors belong to P. Assume p1 = 2; otherwise there can be no consecutive P-smooth numbers. Lehmer's method involves solving the Pell equation
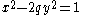
for each P-smooth square-free number q other than 2. Each such number q is generated as a product of a subset of P, so there are 2k-1 Pell equations to solve. For each such equation, let xi,yi be the generated solutions, for i in the range [1,max(3,(pk+1)/2)], where pk is the largest of the primes in P.
Then, as Lehmer shows, all consecutive pairs of P-smooth numbers are of the form (xi - 1)/2, (xi + 1)/2. Thus one can find all such pairs by testing the numbers of this form for P-smoothness.
Example
To find the ten consecutive pairs of {2,3,5}-smooth numbersRegular number
Regular numbers are numbers that evenly divide powers of 60. As an example, 602 = 3600 = 48 × 75, so both 48 and 75 are divisors of a power of 60...
giving the superparticular ratios for just tuning, let P = {2,3,5}. There are seven P-smooth squarefree numbers q (omitting the eighth P-smooth squarefree number, 2): 1, 3, 5, 6, 10, 15, and 30, each of which leads to a Pell equation. The number of solutions per Pell equation required by Lehmer's method is max(3,(5+1)/2) = 3, so this method generates three solutions to each Pell equation, as follows.
- For q = 1, the first three solutions to the Pell equation x2 - 2y2 = 1 are (3,2), (17,12), and (99,70). Thus, for each of the three values xi = 3, 17, and 99, Lehmer's method tests the pair (xi-1)/2,(xi+1)/2 for smoothness; the three pairs to be tested are (1,2), (8,9), and (49,50). Both (1,2) and (8,9) are pairs of consecutive P-smooth numbers, but (49,50) is not, as 49 has 7 as a prime factor.
- For q = 3, the first three solutions to the Pell equation x2 - 6y2 = 1 are (5,2), (49,20), and (485,198). From the three values xi = 5, 49, and 485 Lehmer's method forms the three candidate pairs of consecutive numbers (xi-1)/2,(xi+1)/2: (3,2), (25,24), and (243,242). Of these, (3,2) and (25,24) are pairs of consecutive P-smooth numbers but (243,242) is not.
- For q = 5, the first three solutions to the Pell equation x2 - 10y2 = 1 are (19,6), (721,228), and (27379,8658). The Pell solution (19,6) leads to the pair of consecutive P-smooth numbers (9,10); the other two solutions to the Pell equation do not lead to P-smooth pairs.
- For q = 6, the first three solutions to the Pell equation x2 - 12y2 = 1 are (7,2), (97,28), and (1351,390). The Pell solution (7,2) leads to the pair of consecutive P-smooth numbers (3,4).
- For q = 10, the first three solutions to the Pell equation x2 - 20y2 = 1 are (9,2), (161,36), and (2889,646). The Pell solution (9,2) leads to the pair of consecutive P-smooth numbers (4,5) and the Pell solution (161,36) leads to the pair of consecutive P-smooth numbers (80,81).
- For q = 15, the first three solutions to the Pell equation x2 - 30y2 = 1 are (11,2), (241,44), and (5291,966). The Pell solution (11,2) leads to the pair of consecutive P-smooth numbers (5,6).
- For q = 30, the first three solutions to the Pell equation x2 - 60y2 = 1 are (31,4), (1921,248), and (119071,15372). The Pell solution (31,4) leads to the pair of consecutive P-smooth numbers (15,16).
Counting solutions
Størmer's original result can be used to show that the number of consecutive pairs of integers that are smooth with respect to a set of k primes is at most 3k − 2k. Lehmer's result produces a tighter bound for sets of small primes: (2k − 1) × max(3,(pk+1)/2).The number of consecutive pairs of integers that are smooth with respect to the first k primes are
- 1, 4, 10, 23, 40, 68, 108, 167, 241, 345, ... .
The largest integer from all these pairs, for each k, is
- 2, 9, 81, 4375, 9801, 123201, 336141, 11859211, ... .
OEIS also lists the number of pairs of this type where the larger of the two integers in the pair is square or triangular
Triangular number
A triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n...
, as both types of pair arise frequently.
Generalizations and applications
Chein (1976) used Størmer's method to prove Catalan's conjecture on the nonexistence of consecutive perfect powers (other than 8,9) in the case where one of the two powers is a squareSquare number
In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
.
Mabkhout (1993) proved that every number x4 + 1, for x > 3, has a prime factor greater than or equal to 137. Størmer's theorem is an important part of his proof, in which he reduces the problem to the solution of 128 Pell equations.
Several authors have extended Størmer's work by providing methods for listing the solutions to more general diophantine equation
Diophantine equation
In mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
s, or by providing more general divisibility criteria for the solutions to Pell equations.

