Stieltjes transformation
Encyclopedia
In mathematics, the Stieltjes transformation Sρ(z) of a measure of density ρ on a real interval I is the function of the complex variable z defined outside I by the formula
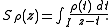
Under certain conditions we can reconstitute the density function ρ starting from its Stieltjes transformation thanks to the inverse formula of Stieltjes-Perron. For example, if the density ρ is continuous throughout I, one will have inside this interval
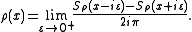
of any order defined for each integer by the equality
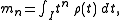
then the Stieltjes transformation of ρ admits for each integer n the asymptotic
expansion in the neighbourhood of infinity given by
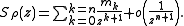
Under certain conditions the complete expansion as a Laurent series
can be obtained:
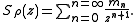
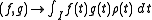defines an inner product on the space of continuous function
s on the interval I.
If {Pn} is a sequence of orthogonal polynomials
for this product, we can create the sequence of associated secondary polynomials by the formula
It appears that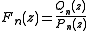
is a Padé approximation of Sρ(z) in a neighbourhood of infinity, in the sense that
Since these two sequences of polynomials satisfy the same recurrence relation in three terms, we can develop a continued fraction
for the Stieltjes transformation whose successive convergents
are the fractions Fn(z).
The Stieltjes transformation can also be used to construct from the density ρ an effective measure for transforming the secondary polynomials into an orthogonal system. (For more details see the article secondary measure
.)
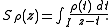
Under certain conditions we can reconstitute the density function ρ starting from its Stieltjes transformation thanks to the inverse formula of Stieltjes-Perron. For example, if the density ρ is continuous throughout I, one will have inside this interval
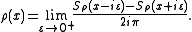
Connections with moments of measures
If the measure of density ρ has momentsMoment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
of any order defined for each integer by the equality
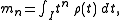
then the Stieltjes transformation of ρ admits for each integer n the asymptotic
Asymptotic analysis
In mathematical analysis, asymptotic analysis is a method of describing limiting behavior. The methodology has applications across science. Examples are...
expansion in the neighbourhood of infinity given by
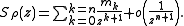
Under certain conditions the complete expansion as a Laurent series
Laurent series
In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
can be obtained:
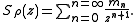
Relationships to orthogonal polynomials
The correspondence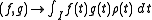 defines an inner product on the space of continuous functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s on the interval I.
If {Pn} is a sequence of orthogonal polynomials
Orthogonal polynomials
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
for this product, we can create the sequence of associated secondary polynomials by the formula
It appears that
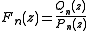is a Padé approximation of Sρ(z) in a neighbourhood of infinity, in the sense that
Since these two sequences of polynomials satisfy the same recurrence relation in three terms, we can develop a continued fraction
Generalized continued fraction
In complex analysis, a branch of mathematics, a generalized continued fraction is a generalization of regular continued fractions in canonical form, in which the partial numerators and partial denominators can assume arbitrary real or complex values....
for the Stieltjes transformation whose successive convergents
Convergent (continued fraction)
A convergent is one of a sequence of values obtained by evaluating successive truncations of a continued fraction The nth convergent is also known as the nth approximant of a continued fraction.-Representation of real numbers:...
are the fractions Fn(z).
The Stieltjes transformation can also be used to construct from the density ρ an effective measure for transforming the secondary polynomials into an orthogonal system. (For more details see the article secondary measure
Secondary measure
In mathematics, the secondary measure associated with a measure of positive density \rho when there is one, is a measure of positive density \mu, turning the secondary polynomials associated with the orthogonal polynomials for \rho into an orthogonal system....
.)