
Stabilizer code
Encyclopedia
The theory of quantum error correction
plays a prominent role in the practical realization and engineering of
quantum computing and quantum communication devices. The first quantum
error-correcting codes are strikingly similar to classical block codes in their
operation and performance. Quantum error-correcting codes restore a noisy,
decohered quantum state to a pure quantum state. A
stabilizer quantum error-correcting code appends ancilla qubits
to qubits that we want to protect. A unitary encoding circuit rotates the
global state into a subspace of a larger Hilbert space
. This highly entangled,
encoded state corrects for local noisy errors. A quantum error-correcting code makes quantum computation
and quantum communication practical by providing a way for a sender and
receiver to simulate a noiseless qubit channel given a noisy qubit channel
that has a particular error model.
The stabilizer theory of quantum error correction
allows one to import some
classical binary or quaternary codes for use as a quantum code. The only
"catch" when importing is that the
classical code must satisfy the dual-containing or self-orthogonality
constraint. Researchers have found many examples of classical codes satisfying
this constraint, but most classical codes do not. Nevertheless, it is still useful to import classical codes in this way (though, see how the entanglement-assisted stabilizer formalism
overcomes this difficulty).
the Pauli group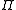 in formulating quantum error-correcting codes. The set
in formulating quantum error-correcting codes. The set
 consists of the Pauli operators:
consists of the Pauli operators: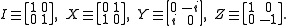
The above operators act on a single qubit
---a state represented by a vector in a two-dimensional
Hilbert space
. Operators in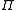 have eigenvalues
have eigenvalues 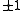 and either commute
and either commute
or anti-commute. The set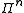 consists of
consists of  -fold tensor product
-fold tensor product
s of
Pauli operators: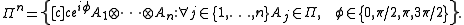
Elements of act on a quantum register of
act on a quantum register of  qubit
qubit
s. We
occasionally omit tensor product
symbols in what follows so that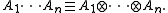
The -fold Pauli group
-fold Pauli group
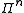 plays an important role for both the encoding circuit and the
plays an important role for both the encoding circuit and the
error-correction procedure of a quantum stabilizer code over qubit
qubit
s.
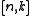 stabilizer quantum error-correcting
stabilizer quantum error-correcting
code to encode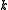 logical qubits into
logical qubits into  physical qubits. The rate of such a
physical qubits. The rate of such a
code is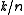 . Its stabilizer
. Its stabilizer 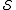 is an abelian
is an abelian
subgroup
of the
 -fold Pauli group
-fold Pauli group  :
: 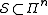 .
. 
does not contain the operator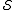 . The simultaneous
. The simultaneous
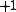 -eigenspace of the operators constitutes the codespace. The
-eigenspace of the operators constitutes the codespace. The
codespace has dimension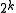 so that we can encode
so that we can encode 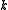 qubit
qubit
s into it. The
stabilizer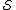 has a minimal representation
has a minimal representation
in terms of
independent generators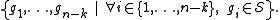
The generators are
independent in the sense that none of them is a product of any other two (up
to a global phase). The operators function in the same
function in the same
way as a parity check matrix does for a classical linear block code.
suffices to correct a discrete
error set with support
in the Pauli group
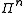 . Suppose that the errors affecting an
. Suppose that the errors affecting an
encoded quantum state are a subset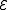 of the Pauli group
of the Pauli group 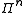 :
: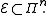
An error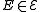 that affects an
that affects an
encoded quantum state either commute
s or anticommutes with any particular
element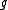 in
in 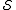 . The error
. The error 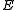 is correctable if it
is correctable if it
anticommutes with an element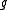 in
in 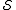 . An anticommuting error
. An anticommuting error
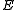 is detectable by measuring each element
is detectable by measuring each element 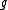 in
in 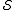 and
and
computing a syndrome
 identifying
identifying 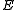 . The syndrome is a binary
. The syndrome is a binary
vector with length
with length  whose elements identify whether the
whose elements identify whether the
error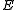 commute
commute
s or anticommutes with each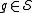 . An error
. An error
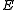 that commute
that commute
s with every element in
in 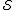 is correctable if
is correctable if
and only if it is in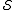 . It corrupts the encoded state if it
. It corrupts the encoded state if it
commutes with every element of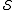 but does not lie in
but does not lie in 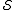 . So we compactly summarize the stabilizer error-correcting conditions: a
. So we compactly summarize the stabilizer error-correcting conditions: a
stabilizer code can correct any errors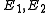 in
in 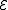 if
if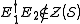
or
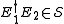
where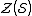 is the centralizer of
is the centralizer of 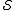 .
.
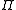 and the binary
and the binary
vector space
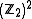 . This mapping gives a
. This mapping gives a
simplification of quantum error correction theory. It represents quantum codes
with binary vector
s and binary operation
s rather than with Pauli operators and
matrix operations respectively.
We first give the mapping for the one-qubit case. Suppose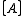
is a set of equivalence classes of an operator
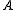 that have the same phase
that have the same phase
: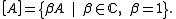
Let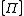 be the set of phase-free Pauli operators where
be the set of phase-free Pauli operators where
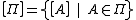 .
.
Define the map as
as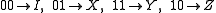
Suppose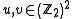 . Let us employ the
. Let us employ the
shorthand and
and 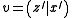 where
where  ,
,  ,
, 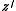 ,
, 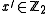 . For
. For
example, suppose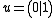 . Then
. Then  . The
. The
map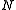 induces an isomorphism
induces an isomorphism
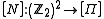 because addition of vectors
because addition of vectors
in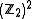 is equivalent to multiplication of
is equivalent to multiplication of
Pauli operators up to a global phase: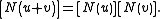
Let denote the symplectic product between two elements
denote the symplectic product between two elements 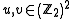 :
: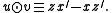
The symplectic product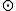 gives the commutation relations of elements of
gives the commutation relations of elements of
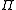 :
: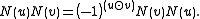
The symplectic product and the mapping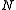 thus give a useful way to phrase
thus give a useful way to phrase
Pauli relations in terms of binary algebra.
The extension of the above definitions and mapping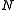 to multiple qubit
to multiple qubit
s is
straightforward. Let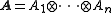 denote an
denote an
arbitrary element of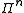 . We can similarly define the phase-free
. We can similarly define the phase-free
 -qubit Pauli group
-qubit Pauli group 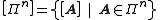 where
where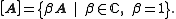
The group operation for the above equivalence class is as follows:
for the above equivalence class is as follows:
The equivalence class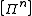 forms a commutative group
forms a commutative group
under operation . Consider the
. Consider the 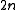 -dimensional vector space
-dimensional vector space
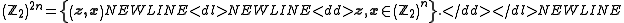
It forms the commutative group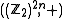 with
with
operation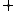 defined as binary vector addition. We employ the notation
defined as binary vector addition. We employ the notation
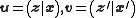 to represent any vectors
to represent any vectors
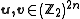 respectively. Each
respectively. Each
vector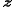 and
and 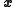 has elements
has elements 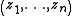 and
and 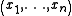 respectively with
respectively with
similar representations for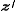 and
and 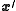 .
.
The \textit{symplectic product}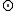 of
of 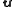 and
and  is
is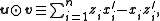
or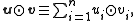
where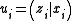 and
and 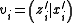 . Let us define a map
. Let us define a map 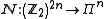 as follows:
as follows: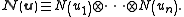
Let
so that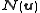 and
and  belong to the same
belong to the same
equivalence class: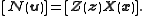
The map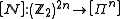 is an isomorphism
is an isomorphism
for the same
reason given as the previous case: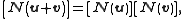
where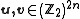 . The symplectic product
. The symplectic product
captures the commutation relations of any operators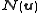 and
and 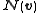 :
: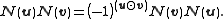
The above binary representation and symplectic algebra are useful in making
the relation between classical linear error correction and quantum error correction
more explicit.
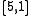 stabilizer code. It encodes
stabilizer code. It encodes 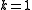 logical qubit
logical qubit
into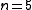 physical qubits and protects against an arbitrary single-qubit
physical qubits and protects against an arbitrary single-qubit
error. Its stabilizer consists of Pauli operators:
Pauli operators: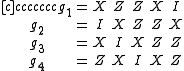
The above operators commute. Therefore the codespace is the simultaneous
+1-eigenspace of the above operators. Suppose a single-qubit error occurs on
the encoded quantum register. A single-qubit error is in the set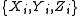 where
where 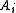 denotes a Pauli error on qubit
denotes a Pauli error on qubit 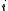 .
.
It is straightforward to verify that any arbitrary single-qubit error has a
unique syndrome. The receiver corrects any single-qubit error by identifying
the syndrome and applying a corrective operation.
Quantum error correction
Quantum error correction is used in quantum computing to protect quantum information from errors due to decoherence and other quantum noise. Quantum error correction is essential if one is to achieve fault-tolerant quantum computation that can deal not only with noise on stored quantum...
plays a prominent role in the practical realization and engineering of
quantum computing and quantum communication devices. The first quantum
error-correcting codes are strikingly similar to classical block codes in their
operation and performance. Quantum error-correcting codes restore a noisy,
decohered quantum state to a pure quantum state. A
stabilizer quantum error-correcting code appends ancilla qubits
to qubits that we want to protect. A unitary encoding circuit rotates the
global state into a subspace of a larger Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. This highly entangled,
encoded state corrects for local noisy errors. A quantum error-correcting code makes quantum computation
and quantum communication practical by providing a way for a sender and
receiver to simulate a noiseless qubit channel given a noisy qubit channel
that has a particular error model.
The stabilizer theory of quantum error correction
Quantum error correction
Quantum error correction is used in quantum computing to protect quantum information from errors due to decoherence and other quantum noise. Quantum error correction is essential if one is to achieve fault-tolerant quantum computation that can deal not only with noise on stored quantum...
allows one to import some
classical binary or quaternary codes for use as a quantum code. The only
"catch" when importing is that the
classical code must satisfy the dual-containing or self-orthogonality
constraint. Researchers have found many examples of classical codes satisfying
this constraint, but most classical codes do not. Nevertheless, it is still useful to import classical codes in this way (though, see how the entanglement-assisted stabilizer formalism
Entanglement-assisted stabilizer formalism
In the theory of quantum communication, the entanglement-assisted stabilizer formalism is a method for protecting quantum information with the help of entanglement shared between a sender and receiver before they transmit quantum data over a quantum communication channel...
overcomes this difficulty).
Mathematical background
The Stabilizer formalism exploits elements ofthe Pauli group
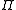 in formulating quantum error-correcting codes. The set
in formulating quantum error-correcting codes. The set consists of the Pauli operators:
consists of the Pauli operators: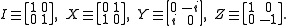
The above operators act on a single qubit
Qubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
---a state represented by a vector in a two-dimensional
Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. Operators in
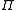 have eigenvalues
have eigenvalues 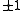 and either commute
and either commuteCommute
Commute, commutation or commutative may refer to:* Commuting, the process of travelling between a place of residence and a place of work* Commutative property, a property of a mathematical operation...
or anti-commute. The set
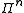 consists of
consists of  -fold tensor product
-fold tensor productTensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
s of
Pauli operators:
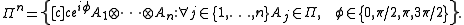
Elements of
 act on a quantum register of
act on a quantum register of  qubit
qubitQubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s. We
occasionally omit tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
symbols in what follows so that
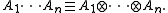
The
 -fold Pauli group
-fold Pauli group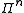 plays an important role for both the encoding circuit and the
plays an important role for both the encoding circuit and theerror-correction procedure of a quantum stabilizer code over
 qubit
qubitQubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s.
Definition
Let us define an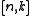 stabilizer quantum error-correcting
stabilizer quantum error-correctingcode to encode
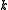 logical qubits into
logical qubits into  physical qubits. The rate of such a
physical qubits. The rate of such acode is
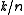 . Its stabilizer
. Its stabilizer 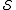 is an abelian
is an abelianAbelian
In mathematics, Abelian refers to any of number of different mathematical concepts named after Niels Henrik Abel:- Group theory :*Abelian group, a group in which the binary operation is commutative...
subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of the
 -fold Pauli group
-fold Pauli group  :
: 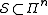 .
. 
does not contain the operator
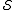 . The simultaneous
. The simultaneous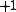 -eigenspace of the operators constitutes the codespace. The
-eigenspace of the operators constitutes the codespace. Thecodespace has dimension
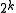 so that we can encode
so that we can encode 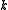 qubit
qubitQubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s into it. The
stabilizer
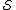 has a minimal representation
has a minimal representationRepresentation (mathematics)
In mathematics, representation is a very general relationship that expresses similarities between objects. Roughly speaking, a collection Y of mathematical objects may be said to represent another collection X of objects, provided that the properties and relationships existing among the...
in terms of

independent generators
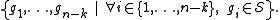
The generators are
independent in the sense that none of them is a product of any other two (up
to a global phase). The operators
 function in the same
function in the sameway as a parity check matrix does for a classical linear block code.
Stabilizer error-correction conditions
One of the fundamental notions in quantum error correction theory is that itsuffices to correct a discrete
Discrete
Discrete in science is the opposite of continuous: something that is separate; distinct; individual.Discrete may refer to:*Discrete particle or quantum in physics, for example in quantum theory...
error set with support
Support (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
in the Pauli group
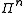 . Suppose that the errors affecting an
. Suppose that the errors affecting anencoded quantum state are a subset
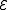 of the Pauli group
of the Pauli group 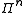 :
: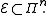
An error
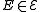 that affects an
that affects anencoded quantum state either commute
Commute
Commute, commutation or commutative may refer to:* Commuting, the process of travelling between a place of residence and a place of work* Commutative property, a property of a mathematical operation...
s or anticommutes with any particular
element
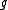 in
in 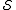 . The error
. The error 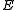 is correctable if it
is correctable if itanticommutes with an element
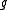 in
in 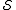 . An anticommuting error
. An anticommuting error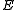 is detectable by measuring each element
is detectable by measuring each element 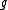 in
in 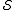 and
andcomputing a syndrome
Syndrome
In medicine and psychology, a syndrome is the association of several clinically recognizable features, signs , symptoms , phenomena or characteristics that often occur together, so that the presence of one or more features alerts the physician to the possible presence of the others...
 identifying
identifying 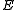 . The syndrome is a binary
. The syndrome is a binaryvector
 with length
with length  whose elements identify whether the
whose elements identify whether theerror
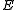 commute
commuteCommute
Commute, commutation or commutative may refer to:* Commuting, the process of travelling between a place of residence and a place of work* Commutative property, a property of a mathematical operation...
s or anticommutes with each
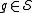 . An error
. An error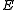 that commute
that commuteCommute
Commute, commutation or commutative may refer to:* Commuting, the process of travelling between a place of residence and a place of work* Commutative property, a property of a mathematical operation...
s with every element
 in
in 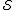 is correctable if
is correctable ifand only if it is in
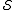 . It corrupts the encoded state if it
. It corrupts the encoded state if itcommutes with every element of
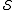 but does not lie in
but does not lie in 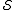 . So we compactly summarize the stabilizer error-correcting conditions: a
. So we compactly summarize the stabilizer error-correcting conditions: astabilizer code can correct any errors
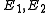 in
in 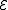 if
if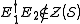
or
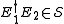
where
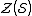 is the centralizer of
is the centralizer of 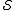 .
.Relation between Pauli group and binary vectors
A simple but useful mapping exists between elements of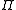 and the binary
and the binaryvector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
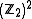 . This mapping gives a
. This mapping gives asimplification of quantum error correction theory. It represents quantum codes
with binary vector
Binary vector
A T-DNA binary system is a pair of plasmids consisting of a binary plasmid and a helper plasmid. The two plasmids are used together to produce genetically modified plants. They are artificial vectors that have both been created from the naturally occurring Ti plasmid found in Agrobacterium...
s and binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s rather than with Pauli operators and
matrix operations respectively.
We first give the mapping for the one-qubit case. Suppose
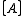
is a set of equivalence classes of an operator
Operator (physics)
In physics, an operator is a function acting on the space of physical states. As a resultof its application on a physical state, another physical state is obtained, very often along withsome extra relevant information....
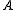 that have the same phase
that have the same phasePhase
-In physics:*Phase , a physically distinctive form of a substance, such as the solid, liquid, and gaseous states of ordinary matter**Phase transition is the transformation of a thermodynamic system from one phase to another*Phase...
:
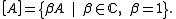
Let
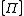 be the set of phase-free Pauli operators where
be the set of phase-free Pauli operators where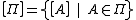 .
.Define the map
 as
as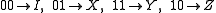
Suppose
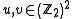 . Let us employ the
. Let us employ theshorthand
 and
and 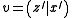 where
where  ,
,  ,
, 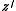 ,
, 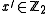 . For
. Forexample, suppose
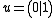 . Then
. Then  . The
. Themap
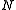 induces an isomorphism
induces an isomorphismIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
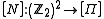 because addition of vectors
because addition of vectorsin
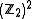 is equivalent to multiplication of
is equivalent to multiplication ofPauli operators up to a global phase:
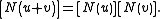
Let
 denote the symplectic product between two elements
denote the symplectic product between two elements 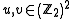 :
: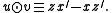
The symplectic product
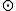 gives the commutation relations of elements of
gives the commutation relations of elements of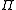 :
: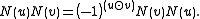
The symplectic product and the mapping
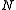 thus give a useful way to phrase
thus give a useful way to phrasePauli relations in terms of binary algebra.
The extension of the above definitions and mapping
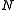 to multiple qubit
to multiple qubitQubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s is
straightforward. Let
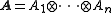 denote an
denote anarbitrary element of
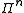 . We can similarly define the phase-free
. We can similarly define the phase-free -qubit Pauli group
-qubit Pauli group 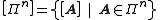 where
where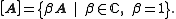
The group operation
 for the above equivalence class is as follows:
for the above equivalence class is as follows:
The equivalence class
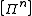 forms a commutative group
forms a commutative groupunder operation
 . Consider the
. Consider the 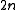 -dimensional vector space
-dimensional vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
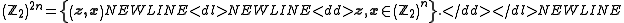
It forms the commutative group
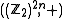 with
withoperation
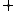 defined as binary vector addition. We employ the notation
defined as binary vector addition. We employ the notation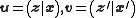 to represent any vectors
to represent any vectors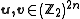 respectively. Each
respectively. Eachvector
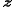 and
and 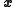 has elements
has elements 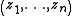 and
and 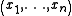 respectively with
respectively withsimilar representations for
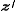 and
and 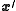 .
.The \textit{symplectic product}
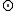 of
of 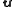 and
and  is
is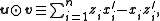
or
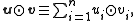
where
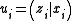 and
and 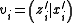 . Let us define a map
. Let us define a map 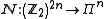 as follows:
as follows: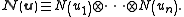
Let

so that
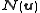 and
and  belong to the same
belong to the sameequivalence class:
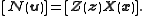
The map
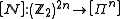 is an isomorphism
is an isomorphismIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
for the same
reason given as the previous case:
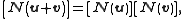
where
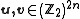 . The symplectic product
. The symplectic productcaptures the commutation relations of any operators
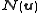 and
and 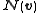 :
: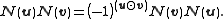
The above binary representation and symplectic algebra are useful in making
the relation between classical linear error correction and quantum error correction
Quantum error correction
Quantum error correction is used in quantum computing to protect quantum information from errors due to decoherence and other quantum noise. Quantum error correction is essential if one is to achieve fault-tolerant quantum computation that can deal not only with noise on stored quantum...
more explicit.
Example of a stabilizer code
An example of a stabilizer code is the five qubit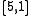 stabilizer code. It encodes
stabilizer code. It encodes 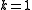 logical qubit
logical qubitinto
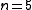 physical qubits and protects against an arbitrary single-qubit
physical qubits and protects against an arbitrary single-qubiterror. Its stabilizer consists of
 Pauli operators:
Pauli operators: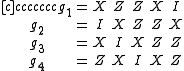
The above operators commute. Therefore the codespace is the simultaneous
+1-eigenspace of the above operators. Suppose a single-qubit error occurs on
the encoded quantum register. A single-qubit error is in the set
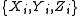 where
where 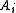 denotes a Pauli error on qubit
denotes a Pauli error on qubit 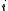 .
.It is straightforward to verify that any arbitrary single-qubit error has a
unique syndrome. The receiver corrects any single-qubit error by identifying
the syndrome and applying a corrective operation.

