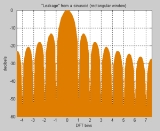
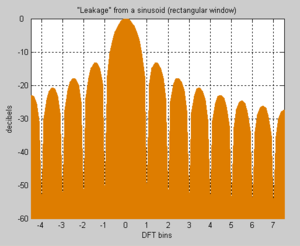
Spectral leakage is an effect in the frequency analysis

Frequency analysis

In cryptanalysis, frequency analysis is the study of the frequency of letters or groups of letters in a ciphertext. The method is used as an aid to breaking classical ciphers....

 of finite-length signals or finite-length segments of infinite signals where it appears as if some energy has "leaked" out of the original signal spectrum into other frequencies.

Typically the leakage shows up as a series of "lobes".
The lobes on an amplitude-vs-frequency DFT graph look similar to the side lobe

Side lobe

In antenna engineering, side lobes or sidelobes are the lobes of the far field radiation pattern that are not the main lobe....

s on an amplitude-vs-angle antenna radiation pattern graph.

Cause

A discrete Fourier transform takes in a finite signal and outputs a finite spectrum: the DFT "bins":
each bin is a frequency, not a range of frequencies. The wavelengths of these bins are the wavelengths that divide the sampling window (such that an integer number of wavelengths occur). The frequencies of these bins are frequencies that divide twice the sampling frequency – thus, if one has a harmonic signal at one of these rates and samples it, it will fall into a single bin, while if a signal that is not one of these rates is sampled, its energy will leak into neighboring bins.

If one now takes an infinite time signal – a sinusoid of a given frequency – and samples it a finite set of points, then, if it is one of this finite set of frequencies, it can be perfectly reconstructed: the DFT can only see a discrete spectrum, an effect likened to looking through a "picket fence", with only the gaps visible. For other frequencies, the DFT gives a combination of these frequencies, which is spectral leakage.
Thus, the spectral leakage is due to the finite frequency resolution of the DFT: a finite signal (a signal defined at a finite set of points) has a finite spectrum.
By contrast, the discrete-time Fourier transform

Discrete-time Fourier transform

In mathematics, the discrete-time Fourier transform is one of the specific forms of Fourier analysis. As such, it transforms one function into another, which is called the frequency domain representation, or simply the "DTFT", of the original function . But the DTFT requires an input function...

 has a continuous spectrum and infinite frequency resolution between 0 and the Nyquist frequency

Nyquist frequency

The Nyquist frequency, named after the Swedish-American engineer Harry Nyquist or the Nyquist–Shannon sampling theorem, is half the sampling frequency of a discrete signal processing system...

, meaning that the frequency of any harmonic signal in this range can be precisely determined, given enough samples.
From the point of view of the DTFT, the cause is the lack of samples in the DFT – it is only a finite time slice of the original infinite time signal: the DFT can be interpreted as the DTFT of the original signal, truncated (via a rectangular filter), then repeated periodically. (Repeating periodically does not change the frequency, just adding the same spectrum at different phases.)

That is, spectral leakage is a feature of the discrete Fourier transform, due to the finite number of sample points – the continuous Fourier transform has perfect frequency resolution – a wave of any frequency can be perfectly reconstructed – and a continuous real line as spectrum, while the discrete-time Fourier transform has aliasing due to discrete but infinite samples – it has continuous but periodic spectrum, but no spectral leakage.

From this perspective, of the DFT as a windowed version of the DTFT, spectral leakage is caused by the frequency response

Frequency response

Frequency response is the quantitative measure of the output spectrum of a system or device in response to a stimulus, and is used to characterize the dynamics of the system. It is a measure of magnitude and phase of the output as a function of frequency, in comparison to the input...

 of the rectangular window: its Fourier transform, the sinc function, has oscillations of periodic width (with periodic zeros), whose log amplitude yield the sidelobes of periodic width (with periodic perfect attenuation) – note that negatives in the frequency domain correspond to polarity inversion (phase shift of 180°).

At the frequencies in the (finite) spectrum of the DFT, there is no leakage, but from the point of view of the frequency response of the rectangular filter, there is always leakage, though at a frequency in the spectrum of the DFT, the nulls (perfect attenuation) fall on the other points of the spectrum of the DFT, and thus the frequency is captured in exactly 1 of the bins.

Window functions

Thus, to reduce the spectral leakage, one uses a window function

Window function

In signal processing, a window function is a mathematical function that is zero-valued outside of some chosen interval. For instance, a function that is constant inside the interval and zero elsewhere is called a rectangular window, which describes the shape of its graphical representation...

 with better frequency response. The ideal window function is one whose frequency response is a Dirac delta function

Dirac delta function

The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...

: each frequency has spectrum only its frequency. This is impossible, as the DFT has but finitely many points of spectrum to capture infinitely many possible frequencies – and in fact the Fourier transform of the Dirac delta is the constant function 1, an infinite rectangle, corresponding to the fact that there is no spectral leakage if one includes data points for infinite time. Instead of a delta function, one has a main lobe and side lobes, as for the rectangular window, but it may have a different shape.

The main criteria are:

• The width of the main lobe,
• the attenuation at the maximum height of a side lobe, generally the first side lobe (the side lobe level), and
• the rate at which the peaks of the side lobes fall-off (the side lobe fall-off).

Ideally:

• the main lobe will be narrow (corresponding to high frequency resolution),
• the first side lobe will be low (corresponding to noise suppression), and
• the side lobes fall-off rapidly.

As multiplying with a window function may increase but not decrease the spectral energy is conserved, there is thus a trade-off between these.

Non-rectangular window functions actually increase the total leakage, but they can also redistribute it to places where it does the least harm, depending on the application. In general, they control the trade-off between resolving comparable strength signals with similar frequencies and resolving disparate strength signals with dissimilar frequencies: one speaks of "high resolution" versus "high dynamic range" windows.

Mathematics

The mathematics of spectral leakage can be understood by computing the discrete Fourier transform of an oscillating exponential signal. For the signal where is any number not necessarily an integer, the discrete Fourier transform is



Taking the modulus square gives



Therefore, power leaks into bins with relatively close to . Spectral leakage of a sinusoidal signal can be computed by breaking the sinusoid into complex exponential components and then applying the results cited here.

See also

• DTFT#Finite-length sequences
• Knife-edge effect
  Knife-edge effect
  In electromagnetic wave propagation, the knife-edge effect or edge diffraction is a redirection by diffraction of a portion of the incident radiation that strikes a well-defined obstacle such as a mountain range or the edge of a building....
  
  , spatial analog of truncation
• Window function
  Window function
  In signal processing, a window function is a mathematical function that is zero-valued outside of some chosen interval. For instance, a function that is constant inside the interval and zero elsewhere is called a rectangular window, which describes the shape of its graphical representation...