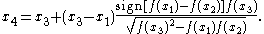Ridders' method
Encyclopedia
In numerical analysis
, Ridders' method is a root-finding algorithm
based on the false position method
and the use of an exponential function
to successively approximate a root of a function
f.
Ridders' method is simpler than Brent's method
but Press et al. (2007) claim that it usually performs about as well. The formula below converges quadratically, which implies that the number of additional significant digits found at each step approximately doubles; but the function has to be evaluated twice for each step, so the overall order of convergence of the method is √2. The method is due to Ridders (1979).
The method can be summarized by the formula (equation 9.2.4 from Press et al.)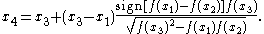
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, Ridders' method is a root-finding algorithm
Root-finding algorithm
A root-finding algorithm is a numerical method, or algorithm, for finding a value x such that f = 0, for a given function f. Such an x is called a root of the function f....
based on the false position method
False position method
The false position method or regula falsi method is a term for problem-solving methods in algebra and calculus. In simple terms, these methods begin by attempting to evaluate a problem using test values for the variables, and then adjust the values accordingly.-Algebra:In algebra, the false...
and the use of an exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
to successively approximate a root of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f.
Ridders' method is simpler than Brent's method
Brent's method
In numerical analysis, Brent's method is a complicated but popular root-finding algorithm combining the bisection method, the secant method and inverse quadratic interpolation. It has the reliability of bisection but it can be as quick as some of the less reliable methods...
but Press et al. (2007) claim that it usually performs about as well. The formula below converges quadratically, which implies that the number of additional significant digits found at each step approximately doubles; but the function has to be evaluated twice for each step, so the overall order of convergence of the method is √2. The method is due to Ridders (1979).
Method
Press et al. (2007) describe the method as follows. Given two values of the independent variable, x1 and x2, which are on two different sides of the root being sought, the method begins by evaluating the function at the midpoint x3 between the two points. One then finds the unique exponential function of the form eax which, when multiplied by f, transforms the function at the three points into a straight line. The false position method is then applied to the transformed values, leading to a new value x4, between x1 and x2, which can be used as one of the two bracketing values in the next step of the iteration.The method can be summarized by the formula (equation 9.2.4 from Press et al.)