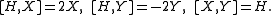Representation theory of SL2(R)
Encyclopedia
In mathematics
, the main results concerning irreducible unitary representation
s of the Lie group
SL(2,R) are due to Gelfand
and Naimark
(1946), V. Bargmann (1947), and Harish-Chandra
(1952).
, which means that they satisfy the relations
One way of doing this is as follows:
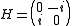corresponding to the subgroup K of matrices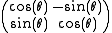 
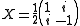
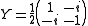
The Casimir operator Ω is defined to be
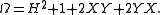
It generates the center of the universal enveloping algebra
of the complexified Lie algebra of SL2(R). The Casimir element acts on any irreducible representation as multiplication by some complex scalar μ2. Thus in the case of the Lie algebra sl2, the infinitesimal character
of an irreducible representation is specified by one complex number.
The center Z of the group SL2(R) is a cyclic group {I,-I} of order 2, consisting of the identity matrix and its negative. On any irreducible representation, the center either acts trivially, or by the non trivial character of Z, which represents the matrix -I by multiplication by -1 in the representation space. Correspondingly, one speaks of the trivial or nontrivial central character.
The central character and the infinitesimal character of an irreducible representation of any reductive Lie group are important invariants of the representation. In the case of irreducible admissible representations of SL(2,R), it turns out that, generically, there is exactly one representation, up to an isomorphism, with the specified central and infinitesimal characters. In the exceptional cases there are two or three representations with the prescribed parameters, all of which have been determined.
. An irreducible finite dimensional representation of a noncompact simple Lie group
of dimension greater than 1 is never unitary. Thus this construction produces only one unitary representation of SL(2,R), the trivial representation.
The finite-dimensional representation theory of the noncompact group SL(2,R) is equivalent to the representation theory of SU(2)
, its compact form, essentially because their Lie algebras have the same complexification and they are "algebraically simply connected". (More precisely the group SU(2) is simply connected and SL(2,R) is not, but has no non-trivial algebraic central extensions.) However, in the general infinite-dimensional case, there is no close correspondence between representations of a group and the representations of its Lie algebra. In fact, it follows from the Peter-Weyl theorem that all irreducible representations of the compact Lie group SU(2) are finite-dimensional and unitary. The situation with SL(2,R) is completely different: it possesses infinite-dimensional irreducible representations, some of which are unitary, and some are not.
. In the case of the group SL(2,R), there is up to conjugacy only one proper parabolic subgroup, the Borel subgroup
of the upper-triangular matrices of determinant 1. The inducing parameter of an induced principal series representation
is a (possibly non-unitrary) character of the multiplicative group of real numbers, which is specified by choosing ε = ± 1 and a complex number μ. The corresponding principal series representation is denoted Iε,μ. It turns out that ε is the central character of the induced representation and the complex number μ may be identified with the infinitesimal character
via the Harish-Chandra isomorphism.
The principal series representation Iε,μ (or more precisely its Harish-Chandra module of K-finite elements) admits a basis consisting of elements wj, where the index j runs through the even integers if ε=1 and the odd integers if ε=-1. The action of X, Y, and H is given by the formulas
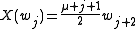
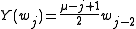
is a subrepresentation of a parabolically induced representation. (This also is true for more general reductive Lie groups and is known as Casselman's subrepresentation theorem.) Thus the irreducible admissible representations of SL(2,R) can be found by decomposing the principal series representations Iε,μ into irreducible components and determining the isomorphisms. We summarize the decompositions as follows:
This gives the following list of irreducible admissible representations:
, the irreducible admissible representations are parametrized by certain tempered representations of Levi subgroups M of parabolic subgroups P=MAN. This works as follows:
Of these, the two limit of discrete series representations, the discrete series representations, and the two families of principal series representations are tempered
, while the trivial and complementary series representations are not tempered.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the main results concerning irreducible unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
s of the Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
SL(2,R) are due to Gelfand
Israel Gelfand
Israel Moiseevich Gelfand, also written Israïl Moyseyovich Gel'fand, or Izrail M. Gelfand was a Soviet mathematician who made major contributions to many branches of mathematics, including group theory, representation theory and functional analysis...
and Naimark
Mark Naimark
Mark Aronovich Naimark was a Soviet mathematician.He was born in Odessa, Russian Empire into a Jewish family and died in Moscow, USSR...
(1946), V. Bargmann (1947), and Harish-Chandra
Harish-Chandra
Harish-Chandra was an Indian mathematician, who did fundamental work in representation theory, especially Harmonic analysis on semisimple Lie groups. -Life:...
(1952).
Structure of the complexified Lie algebra
We choose a basis H, X, Y for the complexification of the Lie algebra of SL(2,R) so that iH generates the Lie algebra of a compact Cartan subgroup K (so in particular unitary representations split as a sum of eigenspaces of H), and {H,X,Y} is an sl2-tripleSl2-triple
In the theory of Lie algebras, an sl2-triple is a triple of elements of a Lie algebra that satisfy the commutation relations between the standard generators of the special linear Lie algebra sl2...
, which means that they satisfy the relations
One way of doing this is as follows:
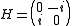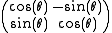
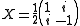
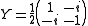
corresponding to the subgroup K of matrices The Casimir operator Ω is defined to be
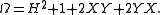
It generates the center of the universal enveloping algebra
Universal enveloping algebra
In mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
of the complexified Lie algebra of SL2(R). The Casimir element acts on any irreducible representation as multiplication by some complex scalar μ2. Thus in the case of the Lie algebra sl2, the infinitesimal character
Infinitesimal character
In mathematics, the infinitesimal character of an irreducible representation ρ of a semisimple Lie group G on a vector space V is, roughly speaking, a mapping to scalars that encodes the process of first differentiating and then diagonalizing the representation...
of an irreducible representation is specified by one complex number.
The center Z of the group SL2(R) is a cyclic group {I,-I} of order 2, consisting of the identity matrix and its negative. On any irreducible representation, the center either acts trivially, or by the non trivial character of Z, which represents the matrix -I by multiplication by -1 in the representation space. Correspondingly, one speaks of the trivial or nontrivial central character.
The central character and the infinitesimal character of an irreducible representation of any reductive Lie group are important invariants of the representation. In the case of irreducible admissible representations of SL(2,R), it turns out that, generically, there is exactly one representation, up to an isomorphism, with the specified central and infinitesimal characters. In the exceptional cases there are two or three representations with the prescribed parameters, all of which have been determined.
Finite dimensional representations
For each nonnegative integer n, the group SL(2,R) has an irreducible representation of dimension n+1, which is unique up to an isomorphism. This representation can be constructed in the space of homogeneous polynomials of degree n in two variables. The case n=0 corresponds to the trivial representationTrivial representation
In the mathematical field of representation theory, a trivial representation is a representation of a group G on which all elements of G act as the identity mapping of V...
. An irreducible finite dimensional representation of a noncompact simple Lie group
Simple Lie group
In group theory, a simple Lie group is a connected non-abelian Lie group G which does not have nontrivial connected normal subgroups.A simple Lie algebra is a non-abelian Lie algebra whose only ideals are 0 and itself...
of dimension greater than 1 is never unitary. Thus this construction produces only one unitary representation of SL(2,R), the trivial representation.
The finite-dimensional representation theory of the noncompact group SL(2,R) is equivalent to the representation theory of SU(2)
Representation theory of SU(2)
In the study of the representation theory of Lie groups, the study of representations of SU is fundamental to the study of representations of semisimple Lie groups. It is the first case of a Lie group that is both a compact group and a non-abelian group...
, its compact form, essentially because their Lie algebras have the same complexification and they are "algebraically simply connected". (More precisely the group SU(2) is simply connected and SL(2,R) is not, but has no non-trivial algebraic central extensions.) However, in the general infinite-dimensional case, there is no close correspondence between representations of a group and the representations of its Lie algebra. In fact, it follows from the Peter-Weyl theorem that all irreducible representations of the compact Lie group SU(2) are finite-dimensional and unitary. The situation with SL(2,R) is completely different: it possesses infinite-dimensional irreducible representations, some of which are unitary, and some are not.
Principal series representations
A major technique of constructing representations of a reductive Lie group is the method of parabolic inductionParabolic induction
In mathematics, parabolic induction is a method of constructing representations of a reductive group from representations of its parabolic subgroups....
. In the case of the group SL(2,R), there is up to conjugacy only one proper parabolic subgroup, the Borel subgroup
Borel subgroup
In the theory of algebraic groups, a Borel subgroup of an algebraic group G is a maximal Zariski closed and connected solvable algebraic subgroup.For example, in the group GLn ,...
of the upper-triangular matrices of determinant 1. The inducing parameter of an induced principal series representation
Principal series representation
In mathematics, the principal series representations of certain kinds of topological group G occur in the case where G is not a compact group. There, by analogy with spectral theory, one expects that the regular representation of G will decompose according to some kind of continuous spectrum, of...
is a (possibly non-unitrary) character of the multiplicative group of real numbers, which is specified by choosing ε = ± 1 and a complex number μ. The corresponding principal series representation is denoted Iε,μ. It turns out that ε is the central character of the induced representation and the complex number μ may be identified with the infinitesimal character
Infinitesimal character
In mathematics, the infinitesimal character of an irreducible representation ρ of a semisimple Lie group G on a vector space V is, roughly speaking, a mapping to scalars that encodes the process of first differentiating and then diagonalizing the representation...
via the Harish-Chandra isomorphism.
The principal series representation Iε,μ (or more precisely its Harish-Chandra module of K-finite elements) admits a basis consisting of elements wj, where the index j runs through the even integers if ε=1 and the odd integers if ε=-1. The action of X, Y, and H is given by the formulas
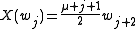
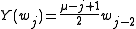
Admissible representations
Using the fact that it is an eigenvector of the Casimir operator and has an eigenvector for H, it follows easily that any irreducible admissible representationAdmissible representation
In mathematics, admissible representations are a well-behaved class of representations used in the representation theory of reductive Lie groups and locally compact totally disconnected groups. They were introduced by Harish-Chandra....
is a subrepresentation of a parabolically induced representation. (This also is true for more general reductive Lie groups and is known as Casselman's subrepresentation theorem.) Thus the irreducible admissible representations of SL(2,R) can be found by decomposing the principal series representations Iε,μ into irreducible components and determining the isomorphisms. We summarize the decompositions as follows:
- Iε,μ is reducible if and only if μ is an integer and ε=−(−1)μ. If Iε,μ is irreducible then it is isomorphic to Iε,−μ.
- I−1, 0 splits as the direct sum Iε,0 = D+0 + D−0 of two irreducible representations, called limit of discrete series representations. D+0 has a basis wj for j≥1, and D-0 has a basis wj for j≤−1,
- If Iε,μ is reducible with μ>0 (so ε=−(−1)μ) then it has a unique irreducible quotient which has finite dimension μ, and the kernel is the sum of two discrete series representations D+μ + D−μ. The representation Dμ has a basis wμ+j for j≥1, and D-μ has a basis w−μ−j for j≤−1.
- If Iε,μ is reducible with μ<0 (so ε=−(−1)μ) then it has a unique irreducible subrepresentation, which has finite dimension μ, and the quotient is the sum of two discrete series representations D+μ + D−μ.
This gives the following list of irreducible admissible representations:
- A finite dimensional representation of dimension μ for each positive integer μ, with central character −(−1)μ.
- Two limit of discrete series representations D+0, D−0, with μ=0 and non-trivial central character.
- Discrete series representations Dμ for μ a non-zero integer, with central character −(−1)ε
- Two families of irreducible principal series representations Iε,μ for ε≠−(−1)μ (where Iε,μ is isomorphic to Iε,−μ).
Relation with the Langlands classification
According to the Langlands classificationLanglands classification
In mathematics, the Langlands classification is a classification of irreducible representations of a reductive Lie group G, suggested by Robert Langlands...
, the irreducible admissible representations are parametrized by certain tempered representations of Levi subgroups M of parabolic subgroups P=MAN. This works as follows:
- The discrete series, limit of discrete series, and unitary principle series representations Iε,μ with μ imaginary are already tempered, so in these cases the parabolic subgroup P is SL2 itself.
- The finite dimensional representations and the representations Iε,μ for ℜμ>0, μ not an integer or ε≠−(−1)μ are the irreducible quotients of the principal series representations Iε,μ for ℜμ>0, which are induced from tempered representations of the parabolic subgroup P=MAN of upper triangular matrices, with A the positive diagonal matrices and M the center of order 2. For μ a positive integer and ε=−(−1)μ the principal series representation has a finite dimensional representation as its irreducible quotient, and otherwise it is already irreducible.
Unitary representations
The irreducible unitary representations can be found by checking which of the irreducible admissible representations admit an invariant positively-definite Hermitian form. This results in the following list of unitary representations of SL(2,R):- The trivial representation (the only finite-dimensional representation in this list).
- The two limit of discrete series representations D+0, D−0.
- The discrete series representationDiscrete series representationIn mathematics, a discrete series representation is an irreducible unitary representation of a locally compact topological group G that is a subrepresentation of the left regular representation of G on L²...
s Dk, indexed by non-zero integers k. They are all distinct. - The two families of irreducible principal series representationPrincipal series representationIn mathematics, the principal series representations of certain kinds of topological group G occur in the case where G is not a compact group. There, by analogy with spectral theory, one expects that the regular representation of G will decompose according to some kind of continuous spectrum, of...
, consisting of the spherical principal series I+,iμ indexed by the real numbers μ, and the non-spherical unitary principal series I-,iμ indexed by the non-zero real numbers μ. The representation with parameter μ is isomorphic to the one with parameter −μ, and there are no further isomorphisms between them. - The complementary series representationComplementary series representationIn mathematics, complementary series representations of a reductive real or p-adic Lie groups are certain irreducible unitary representations that are not tempered and do not appear in the decomposition of the regular representation into irreducible representations.They are rather mysterious: they...
s I+,μ for 0<|μ|<1. The representation with parameter μ is isomorphic to the one with parameter −μ, and there are no further isomorphisms between them.
Of these, the two limit of discrete series representations, the discrete series representations, and the two families of principal series representations are tempered
Tempered representation
In mathematics, a tempered representation of a linear semisimple Lie group is a representation that has a basis whose matrix coefficients lie in the Lp spacefor any ε > 0.-Formulation:...
, while the trivial and complementary series representations are not tempered.
Minicourse
The videos of the SL(2,R) Summer School in Utah in June 2006 provides a great introduction on master level: Homepage of Utah Summer School 2006.See also
- spin (physics)Spin (physics)In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
- Representation theory of SU(2)Representation theory of SU(2)In the study of the representation theory of Lie groups, the study of representations of SU is fundamental to the study of representations of semisimple Lie groups. It is the first case of a Lie group that is both a compact group and a non-abelian group...