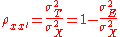Reliability (statistics)
Encyclopedia
In statistics
, reliability is the consistency of a set of measurements or of a measuring instrument, often used to describe a test. Reliability is inversely related to random error
.
, reliability is analogous to precision, while validity is analogous to accuracy.
An example often used to illustrate the difference between reliability and validity in the experimental sciences involves a common bathroom scale. If someone who is 200 pounds steps on a scale 10 times and gets readings of 15, 250, 95, 140, etc., the scale is not reliable. If the scale consistently reads "150", then it is reliable, but not valid. If it reads "200" each time, then the measurement is both reliable and valid. This is what is meant by the statement, "Reliability is necessary but not sufficient for validity."
between two administrations of the same measure: see also item-total correlation
. In the alternate forms method, reliability is estimated by the Pearson product-moment correlation coefficient of two different forms of a measure, usually administered together. Single-administration methods include split-half and internal consistency
. The split-half method treats the two halves of a measure as alternate forms. This "halves reliability" estimate is then stepped up to the full test length using the Spearman–Brown prediction formula. The most common internal consistency measure is Cronbach's alpha
, which is usually interpreted as the mean of all possible split-half coefficients. Cronbach's alpha is a generalization of an earlier form of estimating internal consistency, Kuder-Richardson Formula 20
.
These measures of reliability differ in their sensitivity to different sources of error and so need not be equal. Also, reliability is a property of the scores of a measure rather than the measure itself and are thus said to be sample dependent. Reliability estimates from one sample might differ from those of a second sample (beyond what might be expected due to sampling variations) if the second sample is drawn from a different population because the true variability is different in this second population. (This is true of measures of all types—yardsticks might measure houses well yet have poor reliability when used to measure the lengths of insects.)
Reliability may be improved by clarity of expression (for written assessments), lengthening the measure, and other informal means. However, formal psychometric analysis, called item analysis, is considered the most effective way to increase reliability. This analysis consists of computation of item difficulties and item discrimination indices, the latter index involving computation of correlations between the items and sum of the item scores of the entire test. If items that are too difficult, too easy, and/or have near-zero or negative discrimination are replaced with better items, the reliability of the measure will increase.
, reliability is defined mathematically as the ratio of the variation of the true score and the variation of the observed score. Or, equivalently, one minus the ratio of the variation of the error score and the variation of the observed score:
where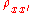 is the symbol for the reliability of the observed score, X;
is the symbol for the reliability of the observed score, X; 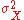 ,
, 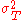 , and
, and  are the variances on the measured, true and error scores respectively. Unfortunately, there is no way to directly observe or calculate the true score, so a variety of methods are used to estimate the reliability of a test.
are the variances on the measured, true and error scores respectively. Unfortunately, there is no way to directly observe or calculate the true score, so a variety of methods are used to estimate the reliability of a test.
Some examples of the methods to estimate reliability include test-retest reliability, internal consistency reliability, and parallel-test reliability. Each method comes at the problem of figuring out the source of error in the test somewhat differently.
extends the concept of reliability from a single index to a function called the information function. The IRT information function is the inverse of the conditional observed score standard error at any given test score.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, reliability is the consistency of a set of measurements or of a measuring instrument, often used to describe a test. Reliability is inversely related to random error
Random error
Random errors are errors in measurement that lead to measurable values being inconsistent when repeated measures of a constant attribute or quantity are taken...
.
Types
There are several general classes of reliability estimates:- Inter-rater reliabilityInter-rater reliabilityIn statistics, inter-rater reliability, inter-rater agreement, or concordance is the degree of agreement among raters. It gives a score of how much homogeneity, or consensus, there is in the ratings given by judges. It is useful in refining the tools given to human judges, for example by...
is the variation in measurements when taken by different persons but with the same method or instruments. - Test-retest reliability is the variation in measurements taken by a single person or instrument on the same item and under the same conditions. This includes intra-rater reliabilityIntra-rater reliabilityIn statistics, intra-rater reliability is the degree of agreement among multiple repetitions of a diagnostic test performed by a single rater.-See also:* Inter-rater reliability* Reliability * Repeatability* Test-retest reliability...
. - Inter-method reliability is the variation in measurements of the same target when taken by a different methods or instruments, but with the same person, or when inter-rater reliability can be ruled out. When dealing with formsForm (document)A form is a document with spaces in which to write or select, for a series of documents with similar contents. The documents usually have the printed parts in common, possibly except for a serial number...
, it may be termed parallel-forms reliability. - Internal consistencyInternal consistencyIn statistics and research, internal consistency is typically a measure based on the correlations between different items on the same test . It measures whether several items that propose to measure the same general construct produce similar scores...
reliability, assesses the consistency of results across items within a test.
Difference from validity
Reliability does not imply validity. That is, a reliable measure is measuring something consistently, but you may not be measuring what you want to be measuring. For example, while there are many reliable tests of specific abilities, not all of them would be valid for predicting, say, job performance. In terms of accuracy and precisionAccuracy and precision
In the fields of science, engineering, industry and statistics, the accuracy of a measurement system is the degree of closeness of measurements of a quantity to that quantity's actual value. The precision of a measurement system, also called reproducibility or repeatability, is the degree to which...
, reliability is analogous to precision, while validity is analogous to accuracy.
An example often used to illustrate the difference between reliability and validity in the experimental sciences involves a common bathroom scale. If someone who is 200 pounds steps on a scale 10 times and gets readings of 15, 250, 95, 140, etc., the scale is not reliable. If the scale consistently reads "150", then it is reliable, but not valid. If it reads "200" each time, then the measurement is both reliable and valid. This is what is meant by the statement, "Reliability is necessary but not sufficient for validity."
Estimation
Reliability may be estimated through a variety of methods that fall into two types: single-administration and multiple-administration. Multiple-administration methods require that two assessments are administered. In the test-retest method, reliability is estimated as the Pearson product-moment correlation coefficientPearson product-moment correlation coefficient
In statistics, the Pearson product-moment correlation coefficient is a measure of the correlation between two variables X and Y, giving a value between +1 and −1 inclusive...
between two administrations of the same measure: see also item-total correlation
Item-total correlation
The item-total correlation test arises in psychometrics in contexts where a number of tests or questions are given to an individual and where the problem is to construct a useful single quantity for each individual that can be used to compare that individual with others in a given population...
. In the alternate forms method, reliability is estimated by the Pearson product-moment correlation coefficient of two different forms of a measure, usually administered together. Single-administration methods include split-half and internal consistency
Internal consistency
In statistics and research, internal consistency is typically a measure based on the correlations between different items on the same test . It measures whether several items that propose to measure the same general construct produce similar scores...
. The split-half method treats the two halves of a measure as alternate forms. This "halves reliability" estimate is then stepped up to the full test length using the Spearman–Brown prediction formula. The most common internal consistency measure is Cronbach's alpha
Cronbach's alpha
Cronbach's \alpha is a coefficient of reliability. It is commonly used as a measure of the internal consistency or reliability of a psychometric test score for a sample of examinees. It was first named alpha by Lee Cronbach in 1951, as he had intended to continue with further coefficients...
, which is usually interpreted as the mean of all possible split-half coefficients. Cronbach's alpha is a generalization of an earlier form of estimating internal consistency, Kuder-Richardson Formula 20
Kuder-Richardson Formula 20
In statistics, the Kuder-Richardson Formula 20 first published in 1937 is a measure of internal consistency reliability for measures with dichotomous choices. It is analogous to Cronbach's α, except Cronbach's α is also used for non-dichotomous measures...
.
These measures of reliability differ in their sensitivity to different sources of error and so need not be equal. Also, reliability is a property of the scores of a measure rather than the measure itself and are thus said to be sample dependent. Reliability estimates from one sample might differ from those of a second sample (beyond what might be expected due to sampling variations) if the second sample is drawn from a different population because the true variability is different in this second population. (This is true of measures of all types—yardsticks might measure houses well yet have poor reliability when used to measure the lengths of insects.)
Reliability may be improved by clarity of expression (for written assessments), lengthening the measure, and other informal means. However, formal psychometric analysis, called item analysis, is considered the most effective way to increase reliability. This analysis consists of computation of item difficulties and item discrimination indices, the latter index involving computation of correlations between the items and sum of the item scores of the entire test. If items that are too difficult, too easy, and/or have near-zero or negative discrimination are replaced with better items, the reliability of the measure will increase.
-
 .
.
-
 . (where
. (where 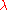 is the failure rate)
is the failure rate)
Classical test theory
In classical test theoryClassical test theory
Classical test theory is a body of related psychometric theory that predict outcomes of psychological testing such as the difficulty of items or the ability of test-takers. Generally speaking, the aim of classical test theory is to understand and improve the reliability of psychological...
, reliability is defined mathematically as the ratio of the variation of the true score and the variation of the observed score. Or, equivalently, one minus the ratio of the variation of the error score and the variation of the observed score:
where
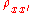 is the symbol for the reliability of the observed score, X;
is the symbol for the reliability of the observed score, X; 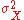 ,
, 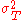 , and
, and  are the variances on the measured, true and error scores respectively. Unfortunately, there is no way to directly observe or calculate the true score, so a variety of methods are used to estimate the reliability of a test.
are the variances on the measured, true and error scores respectively. Unfortunately, there is no way to directly observe or calculate the true score, so a variety of methods are used to estimate the reliability of a test.Some examples of the methods to estimate reliability include test-retest reliability, internal consistency reliability, and parallel-test reliability. Each method comes at the problem of figuring out the source of error in the test somewhat differently.
Item response theory
It was well-known to classical test theorists that measurement precision is not uniform across the scale of measurement. Tests tend to distinguish better for test-takers with moderate trait levels and worse among high- and low-scoring test-takers. Item response theoryItem response theory
In psychometrics, item response theory also known as latent trait theory, strong true score theory, or modern mental test theory, is a paradigm for the design, analysis, and scoring of tests, questionnaires, and similar instruments measuring abilities, attitudes, or other variables. It is based...
extends the concept of reliability from a single index to a function called the information function. The IRT information function is the inverse of the conditional observed score standard error at any given test score.
See also
- Coefficient of variationCoefficient of variationIn probability theory and statistics, the coefficient of variation is a normalized measure of dispersion of a probability distribution. It is also known as unitized risk or the variation coefficient. The absolute value of the CV is sometimes known as relative standard deviation , which is...
- Homogeneity (statistics)Homogeneity (statistics)In statistics, homogeneity and its opposite, heterogeneity, arise in describing the properties of a dataset, or several datasets. They relate to the validity of the often convenient assumption that the statistical properties of any one part of an overall dataset are the same as any other part...
- Internal consistencyInternal consistencyIn statistics and research, internal consistency is typically a measure based on the correlations between different items on the same test . It measures whether several items that propose to measure the same general construct produce similar scores...
- Levels of measurement
- Accuracy and precisionAccuracy and precisionIn the fields of science, engineering, industry and statistics, the accuracy of a measurement system is the degree of closeness of measurements of a quantity to that quantity's actual value. The precision of a measurement system, also called reproducibility or repeatability, is the degree to which...
- Reliability disambiguation page
- Reliability theoryReliability theoryReliability theory describes the probability of a system completing its expected function during an interval of time. It is the basis of reliability engineering, which is an area of study focused on optimizing the reliability, or probability of successful functioning, of systems, such as airplanes,...
- Reliability engineeringReliability engineeringReliability engineering is an engineering field, that deals with the study, evaluation, and life-cycle management of reliability: the ability of a system or component to perform its required functions under stated conditions for a specified period of time. It is often measured as a probability of...
- ReproducibilityReproducibilityReproducibility is the ability of an experiment or study to be accurately reproduced, or replicated, by someone else working independently...
- Validity (statistics)Validity (statistics)In science and statistics, validity has no single agreed definition but generally refers to the extent to which a concept, conclusion or measurement is well-founded and corresponds accurately to the real world. The word "valid" is derived from the Latin validus, meaning strong...