Pseudo-abelian category
Encyclopedia
In mathematics
, specifically in category theory
, a pseudo-abelian category is a category
that is preadditive
and is such that every idempotent has a kernel
. Recall that an idempotent morphism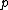
is an endomorphism of an object with the property that 
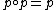. Elementary considerations show that every idempotent then has a cokernel. The pseudo-abelian condition is stronger than preadditivity, but it is weaker than the requirement that every morphism have a kernel and cokernel, as is true for abelian categories.
Synonyms in the literature for pseudo-abelian include pseudoabelian and Karoubian.
, in particular the category Ab of abelian groups, is pseudo-abelian. Indeed, in an abelian category, every morphism has a kernel.
The category of associative rngs
(not rings
!) together with multiplicative morphisms is pseudo-abelian.
A more complicated example is the category of Chow motives. The construction of Chow motives uses the pseudo-abelian completion described below.
construction associates to an arbitrary category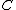
a category 
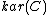together with a functor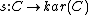
such that the image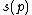
of every idempotent 
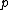in 
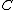splits in 
.
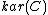When applied to a preadditive category
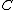, the Karoubi envelope construction yields a pseudo-abelian category 
called the pseudo-abelian completion of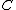
. Moreover, the functor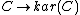
is in fact an additive morphism.
To be precise, given a preadditive category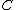
we construct a pseudo-abelian category 
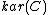in the following way. The objects of 
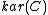are pairs 
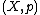where 
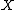is an object of 
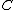and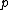 
is an idempotent of 
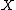. The morphisms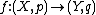
in
are those morphisms
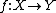
such that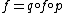
in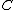 
.
The functor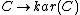
is given by taking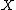
to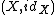 
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a pseudo-abelian category is a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
that is preadditive
Preadditive category
In mathematics, specifically in category theory, a preadditive category is a category that is enriched over the monoidal category of abelian groups...
and is such that every idempotent has a kernel
Kernel (category theory)
In category theory and its applications to other branches of mathematics, kernels are a generalization of the kernels of group homomorphisms, the kernels of module homomorphisms and certain other kernels from algebra...
. Recall that an idempotent morphism
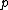is an endomorphism of an object with the property that 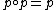. Elementary considerations show that every idempotent then has a cokernel. The pseudo-abelian condition is stronger than preadditivity, but it is weaker than the requirement that every morphism have a kernel and cokernel, as is true for abelian categories.Synonyms in the literature for pseudo-abelian include pseudoabelian and Karoubian.
Examples
Any abelian categoryAbelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
, in particular the category Ab of abelian groups, is pseudo-abelian. Indeed, in an abelian category, every morphism has a kernel.
The category of associative rngs
Rng
Rng can stand for* Random number generator* Rng , an algebraic structure similar to rings but without a multiplicative identity* .rng, the file extension of RELAX NG...
(not rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
!) together with multiplicative morphisms is pseudo-abelian.
A more complicated example is the category of Chow motives. The construction of Chow motives uses the pseudo-abelian completion described below.
Pseudo-abelian completion
The Karoubi envelopeKaroubi envelope
In mathematics the Karoubi envelope of a category C is a classification of the idempotents of C, by means of an auxiliary category. Taking the Karoubi envelope of a preadditive category gives a pseudo-abelian category, hence the construction is sometimes called the pseudo-abelian completion...
construction associates to an arbitrary category
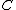a category 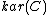together with a functor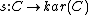such that the image
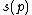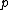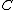of every idempotent in splits in 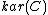.When applied to a preadditive category
Preadditive category
In mathematics, specifically in category theory, a preadditive category is a category that is enriched over the monoidal category of abelian groups...
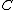, the Karoubi envelope construction yields a pseudo-abelian category called the pseudo-abelian completion of
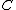. Moreover, the functor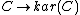is in fact an additive morphism.
To be precise, given a preadditive category
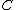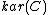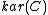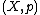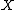we construct a pseudo-abelian category in the following way. The objects of are pairs where is an object of 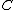and 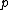is an idempotent of 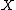. The morphisms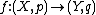in
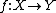
are those morphismssuch that
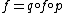in 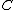.The functor
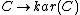
is given by taking
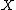to 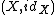.