
Problems in loop theory and quasigroup theory
Encyclopedia
In mathematics
, especially abstract algebra
, loop theory and quasigroup
theory are active research areas with many open problems. As in other areas of mathematics, such problems are often made public at professional conferences and meetings. Many of the problems posed here first appeared in the Loops (Prague) conferences and the Mile High (Denver) conferences.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, loop theory and quasigroup
Quasigroup
In mathematics, especially in abstract algebra, a quasigroup is an algebraic structure resembling a group in the sense that "division" is always possible...
theory are active research areas with many open problems. As in other areas of mathematics, such problems are often made public at professional conferences and meetings. Many of the problems posed here first appeared in the Loops (Prague) conferences and the Mile High (Denver) conferences.
Abelian by cyclic groups resulting in Moufang loops
Let L be a Moufang loopMoufang loopIn mathematics, a Moufang loop is a special kind of algebraic structure. It is similar to a group in many ways but need not be associative. Moufang loops were introduced by Ruth Moufang.-Definition:...
with normal abelianAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
subgroupSubgroupIn group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
(associative subloop) M of odd order such that L/M is a cyclic groupCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order bigger than 3. (i) Is L a groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
? (ii) If the orders of M and L/M are relatively prime, is L a group?
- Proposed: by Michael Kinyon, based on (Chein and Rajah, 2000)
- Comments: The assumption that L/M has order bigger than 3 is important, as there is a (commutative) Moufang loop L of order 81 with normal commutative subgroup of order 27.
(Doro's Conjecture) Does a Moufang loop with trivial nucleus necessarily have normal commutant?
Doro conjectured that a Moufang loopMoufang loopIn mathematics, a Moufang loop is a special kind of algebraic structure. It is similar to a group in many ways but need not be associative. Moufang loops were introduced by Ruth Moufang.-Definition:...
with trivial nucleus has normal commutant. Is it true?
- Proposed: at Milehigh conference on quasigroups, loops, and nonassocitaive systems, Denver 2005
Embedding CMLs of period 3 into alternative algebras
Conjecture: Any finite commutative Moufang loopMoufang loopIn mathematics, a Moufang loop is a special kind of algebraic structure. It is similar to a group in many ways but need not be associative. Moufang loops were introduced by Ruth Moufang.-Definition:...
of period 3 can be embedded into a commutative alternative algebraAlternative algebraIn abstract algebra, an alternative algebra is an algebra in which multiplication need not be associative, only alternative. That is, one must have*x = y*x = y...
.
- Proposed: by Alexander Grishkov at Loops '03, Prague 2003
Minimal presentations for loops M(G,2)
For a group, define
on
x
by
,
,
,
. Find a minimal presentation for the Moufang loop
with respect to a presentation for
.
- Proposed: by Petr Vojtěchovský at Loops '03, Prague 2003
- Comments: Chein showed in (Chein, 1974) that
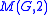 is a Moufang loop that is nonassociative if and only if
is a Moufang loop that is nonassociative if and only if  is nonabelian. Vojtěchovský (Vojtěchovský, 2003) found a minimal presentation for
is nonabelian. Vojtěchovský (Vojtěchovský, 2003) found a minimal presentation for 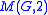 when
when  is a 2-generated group.
is a 2-generated group.
Moufang loops of order p2q3 and pq4
Let p and q be distinct odd primes. If q is not congruent to 1 moduloModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
p, are all Moufang loops of order p2q3 groups? What about pq4?
- Proposed: by Andrew Rajah at Loops '99, Prague 1999
- Comments: The former has been solved by Rajah and Chee (2011) where they showed that for distinct odd primes p1 < ··· < pm < q < r1 < ··· < rn, all Moufang loops of order p12···pm2q3r12···rn2 are groups if and only if q is not congruent to 1 modulo pi for each i.
Moufang loops with non-normal commutant
Is there a Moufang loop whose commutant is not normal?
- Proposed: by Andrew Rajah at Loops '03, Prague 2003
(Phillips' problem) Odd order Moufang loop with trivial nucleus
Is there a Moufang loop of odd order with trivial nucleus?
- Proposed: by Andrew Rajah at Loops '03, Prague 2003
Presentations for finite simple Moufang loops
Find presentations for all nonassociative finite simple Moufang loops in the variety of Moufang loops.
- Proposed: by Petr Vojtěchovský at Loops '03, Prague 2003
- Comments: It is shown in (Vojtěchovský, 2003) that every nonassociative finite simple Moufang loop is generated by 3 elements, with explicit formulas for the generators.
Torsion in free Moufang loops
Let MFn be the freeFree objectIn mathematics, the idea of a free object is one of the basic concepts of abstract algebra. It is a part of universal algebra, in the sense that it relates to all types of algebraic structure . It also has a formulation in terms of category theory, although this is in yet more abstract terms....
Moufang loop with n generators.Conjecture: MF3 is torsion free but MFn with n>4 is not.
- Proposed: by Alexander Grishkov at Loops '03, Prague 2003
Nilpotency degree of the left multiplication group of a left Bol loop
For a left Bol loop Q, find some relation between the nilpotencyNilpotent groupIn mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
degree of the left multiplication group of Q and the structure of Q.
- Proposed: at Milehigh conference on quasigroups, loops, and nonassociative systems, Denver 2005
Are two Bol loops with similar multiplication tables isomorphic?
Let,
be two quasigroups defined on the same underlying set
. The distance
is the number of pairs
in
x
such that
≠
. Call a class of finite quasigroups quadratic if there is a positive real number
such that any two quasigroups
,
of order
from the class satisfying
<

are isomorphic. Are Moufang loops quadratic? Are Bol loop
Bol loopIn mathematics and abstract algebra, a Bol loop is an algebraic structure generalizing the notion of group. Bol loops are named for the Dutch mathematician Gerrit Bol who introduced them in ....
s quadratic?
- Proposed: by Aleš Drápal at Loops '99, Prague 1999
- Comments: Drápal proved in (Drápal, 1992) that groups are quadratic with
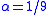 , and in (Drápal, 2000) that 2-groups are quadratic with
, and in (Drápal, 2000) that 2-groups are quadratic with 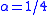 .
.
Campbell-Hausdorff series for analytic Bol loops
Determine the Campbell-Hausdorff series for analytic Bol loops.
- Proposed: by M. A. Akivis and V. V. Goldberg at Loops '99, Prague 1999
- Comments: The problem has been partially solved for local analytic Bruck loops in (Nagy, 2002).
Universally flexible loop that is not middle Bol
A loop is universally flexible if every one of its loop isotopes is flexibleAlternative algebraIn abstract algebra, an alternative algebra is an algebra in which multiplication need not be associative, only alternative. That is, one must have*x = y*x = y...
, that is, satisfies (xy)x=x(yx). A loop is middle Bol if every one of its loop isotopes has the antiautomorphic inverse property, that is, satisfies (xy)-1=y-1x-1. Is there a finite, universally flexible loop that is not middle Bol?
- Proposed: by Michael Kinyon at Loops '03, Prague 2003
Finite simple Bol loop with nontrivial conjugacy classes
Is there a finite simple nonassociative Bol loop with nontrivial conjugacy classes?
- Proposed: by Kenneth W. Johnson and Jonathan D. H. Smith at the 2nd Mile High Conference on Nonassociative Mathematics, Denver 2009
Niemenmaa's conjecture and related problems
Let Q be a loop whose inner mapping group is nilpotent. Is Q nilpotent? Is Q solvable? If Q is also finite, is the multiplication group of Q solvable?
- Proposed: at Loops '03 and '07, Prague 2003 and 2007
- Comments: Niemenmaa conjectures that every loop with nilpotent inner mapping group is nilpotent.
Loops with abelian inner mapping group
Let Q be a loop with abelian inner mapping group. Is Q nilpotent? If so, is there a bound on the nilpotency class of Q? In particular, can the nilpotency class of Q be higher than 3?
- Proposed: at Loops '07, Prague 2007
- Comments: When the inner mapping group Inn(Q) is finite and abelian, then Q is nilpotent (Niemenaa and Kepka). The first question is therefore open only in the infinite case. Call loop Q of Csörgõ type if it is nilpotent of class at least 3, and Inn(Q) is abelian. No loop of Csörgõ type of nilpotency class higher than 3 is known. Loops of Csörgõ type exist (Csörgõ, 2004), Buchsteiner loops of Csörgõ type exist (Csörgõ, Drápal and Kinyon, 2007), and Moufang loops of Csörgõ type exist (Nagy and Vojtěchovský, 2007). On the other hand, there are no groups of Csörgõ type (folklore), there are no commutative Moufang loops of Csörgõ type (Bruck), and there are no Moufang p-loops of Csörgõ type for p>3 (Nagy and Vojtěchovský, 2007).
Number of nilpotent loops up to isomorphism
Determine the number of nilpotent loops of order 24 up to isomorphism.
- Proposed: by Petr Vojtěchovský at the 2nd Mile High Conference on Nonassociative Mathematics, Denver 2009
- Comment: The counts are known for n<24, see (Daly and Vojtěchovský, 2010).
Classification of finite simple paramedial quasigroups
Classify the finite simple paramedial quasigroups.
- Proposed: by Jaroslav Ježek and Tomáš Kepka at Loops '03, Prague 2003
Existence of infinite simple paramedial quasigroups
Are there infinite simple paramedial quasigroups?
- Proposed: by Jaroslav Ježek and Tomáš Kepka at Loops '03, Prague 2003
Minimal isotopically universal varieties of quasigroups
A variety V of quasigroups is isotopically universal if every quasigroup is isotopic to a member of V. Is the variety of loops a minimal isotopically universal variety? Does every isotopically universal variety contain the variety of loops or its parastrophes?
- Proposed: by Tomáš Kepka and Petr Němec at Loops '03, Prague 2003
- Comments: Every quasigroup is isotopic to a loop, hence the variety of loops is isotopically universal.
Small quasigroups with quasigroup core
Does there exist a quasigroup Q of order q=14, 18, 26 or 42 such that the operation * defined on Q by x * y = y - xy is a quasigroup operation?
- Proposed: by Parascovia Syrbu at Loops '03, Prague 2003
- Comments: see (Conselo et al., 1998)
Parity of the number of quasigroups up to isomorphism
Let Q(n) be the number of isomorphism classes of quasigroups of order n. Is Q(n) odd for every n?
- Proposed: by Douglas Stones at 2nd Mile High Conference on Nonassociative Mathematics, Denver 2009
- Comments: The numbers Q(n) are known for 0 < n < 11, and all these are odd.
Uniform construction of latin squares?
Construct a latin square L of order n as follows: Let G = Kn,n be the complete bipartite graph with distinct weights on its n2 edges. Let M1 be the cheapest matching in G, M2 the cheapest matching in G with M1 removed, and so on. Each matching Mi determines a permutation pi of 1, ..., n. Let L be obtained from G by placing the permutation pi into row i of L. Does this procedure result
in a uniform distribution on the space of latin squares of order n?
- Proposed: by Gábor Nagy at the 2nd Mile High Conference on Nonassociative Mathematics, Denver 2009
Bound on the size of multiplication groups
For a loop Q, let Mlt(Q) denote the multiplication group of Q, that is, the group generatedGenerating set of a groupIn abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
by all left and right translations. Is | Mlt( Q ) | < f( | Q | ) for some varietyVariety (universal algebra)In mathematics, specifically universal algebra, a variety of algebras is the class of all algebraic structures of a given signature satisfying a given set of identities. Equivalently, a variety is a class of algebraic structures of the same signature which is closed under the taking of homomorphic...
of loops and for some polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
f?
- Proposed: at the Milehigh conference on quasigroups, loops, and nonassociative systems, Denver 2005
Does every alternative loop have 2-sided inverses?
Does every alternativeAlternative algebraIn abstract algebra, an alternative algebra is an algebra in which multiplication need not be associative, only alternative. That is, one must have*x = y*x = y...
loop, that is, every loop satisfying x(xy)=(xx)y and x(yy)=(xy)y, have 2-sided inverses?
- Proposed: by Warren D. Smith
- Comments: There are infinite alternative loops without 2-sided inverses, cf. (Ormes and Vojtěchovský, 2007)
Finite simple A-loop
Find a nonassociative finite simple A-loop, if such a loop exists.
- Proposed: by Michael Kinyon at Loops '03, Prague 2003
- Comments: It is known that if the order of such a loop is odd, the loop must have exponent p for some primePrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p.
Universality of Osborn loops
A loop is Osborn if it satisfies the identity x((yz)x) = (xλ\y)(zx). Is every Osborn loop universal, that is, is every isotope of an Osborn loop Osborn? If not, is there a nice identity characterizing universal Osborn loops?
- Proposed: by Michael Kinyon at Milehigh conference on quasigroups, loops, and nonassociative systems, Denver 2005
- Comments: Moufang and conjugacy closed loops are Osborn. See (Kinyon, 2005) for more.
Solved problems
The following problems were posed as open at various conferences and have since been solved.Buchsteiner loop that is not conjugacy closed
Is there a Buchsteiner loop that is not conjugacy closed? Is there a finite simple Buchsteiner loop that is not conjugacy closed?
- Proposed: at Milehigh conference on quasigroups, loops, and nonassociative systems, Denver 2005
- Solved by: Piroska Csörgõ, Aleš Drápal, and Michael Kinyon
- Solution: The quotient of a Buchsteiner loop by its nucleus is an abelian group of exponent 4. In particular, no nonassociative Buchsteiner loop can be simple. There exists a Buchsteiner loop of order 128 which is not conjugacy closed.
Classification of Moufang loops of order 64
Classify nonassociative Moufang loops of order 64.
- Proposed: at Milehigh conference on quasigroups, loops, and nonassociative systems, Denver 2005
- Solved by: Gábor P. Nagy and Petr Vojtěchovský
- Solution: There are 4262 nonassociative Moufang loops of order 64. They were found by the method of group modifications in (Vojtěchovský, 2006), and it was shown in (Nagy and Vojtěchovský, 2007) that the list is complete. The latter paper uses a linear-algebraicLinear algebraLinear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
approach to Moufang loop extensions.
Conjugacy closed loop with nonisomorphic one-sided multiplication groups
Construct a conjugacy closed loop whose left multiplication group is not isomorphic to its right multiplication group.
- Proposed: by Aleš Drápal at Loops '03, Prague 2003
- Solved by: Aleš Drápal
- Solution: There is such a loop of order 9. In can be obtained in the
LOOPS package by the command CCLoop(9,1).
Existence of a finite simple Bol loop
Is there a finite simple Bol loopBol loopIn mathematics and abstract algebra, a Bol loop is an algebraic structure generalizing the notion of group. Bol loops are named for the Dutch mathematician Gerrit Bol who introduced them in ....
that is not Moufang?
- Proposed at: Loops '99, Prague 1999
- Solved by: Gábor P. Nagy, 2007.
- Solution: A simple Bol loop that is not Moufang will be called proper.
There are several families of proper simple Bol loops. A smallest proper simple Bol loop is of order 24.
There is also a proper simple Bol loop of exponent 2, and a proper simple Bol loop of odd order.
For details, see (Nagy 2007).
- Comments: The above constructions solved additional two open problems:
- Is there a finite simple Bruck loop that is not Moufang? Yes, since any proper simple Bol loop of exponent 2 is Bruck.
- Is every Bol loop of odd order solvable? No, as witnessed by any proper simple Bol loop of odd order.
Left Bol loop with trivial right nucleus
Is there a finite non-Moufang left Bol loopBol loopIn mathematics and abstract algebra, a Bol loop is an algebraic structure generalizing the notion of group. Bol loops are named for the Dutch mathematician Gerrit Bol who introduced them in ....
with trivial right nucleus?
- Proposed: at Milehigh conference on quasigroups, loops, and nonassociative systems, Denver 2005
- Solved by: Gábor P. Nagy, 2007
- Solution: There is a finite simple left Bol loop of exponent 2 of order 96 with trivial right nucleus. Also, using an exact factorization of the Mathieu groupMathieu groupIn the mathematical field of group theory, the Mathieu groups, named after the French mathematician Émile Léonard Mathieu, are five finite simple groups he discovered and reported in papers in 1861 and 1873; these were the first sporadic simple groups discovered...
M24, it is possible to construct a non-Moufang simple Bol loop which is a G-loopIsotopy of loops- Isotopy of quasigroups :Let and be quasigroups. A quasigroup homotopy from Q to P is a triple of maps from Q to P such that\alpha\circ\beta = \gamma\,for all x, y in Q...
.
Lagrange property for Moufang loops
Does every finite Moufang loop have the strong Lagrange property?
- Proposed: by Orin Chein at Loops '99, Prague 1999
- Solved by: Alexander Grishkov and Andrei Zavarnitsine, 2003
- Solution: Every finite Moufang loop has the strong Lagrange property (SLP). Here is an outline of the proof:
- According to (Chein et al. 2003), it suffices to show SLP for nonassociative finite simple Moufang loops (NFSML).
- It thus suffices to show that the order of a maximal subloop of an NFSML L divides the order of L.
- A countable class of NFSMLs
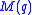 was discovered in (Paige 1956), and no other NSFMLs exist by (Liebeck 1987).
was discovered in (Paige 1956), and no other NSFMLs exist by (Liebeck 1987). - Grishkov and Zavarnitsine matched maximal subloops of loops
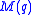 with certain subgroups of groups with triality in (Grishkov and Zavarnitsine, 2003).
with certain subgroups of groups with triality in (Grishkov and Zavarnitsine, 2003).
Quasivariety of cores of Bol loops
Is the class of cores of Bol loops a quasivariety?
- Proposed: by Jonathan D. H. Smith and Alena Vanžurová at Loops '03, Prague 2003
- Solved by: Alena Vanžurová, 2004.
- Solution: No, the class of cores of Bol loops is not closed under subalgebras. Furthermore, the class of cores of groups is not closed under subalgebras. Here is an outline of the proof:
- Cores of abelian groups are medialMedial- Medial magmas :In abstract algebra, a medial magma is a set with a binary operation which satisfies the identity \cdot = \cdot , or more simply, xy\cdot uv = xu\cdot yv...
, by (Romanowska and Smith, 1985), (Rozskowska-Lech, 1999). - The smallest nonabelian group
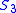 has core containing a submagmaMagma (algebra)In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation M \times M \rightarrow M....
has core containing a submagmaMagma (algebra)In abstract algebra, a magma is a basic kind of algebraic structure. Specifically, a magma consists of a set M equipped with a single binary operation M \times M \rightarrow M....
 of order 4 that is not medial.
of order 4 that is not medial. - If
 is a core of a Bol loop, it is a core of a Bol loop of order 4, hence a core of an abelian group, a contradiction.
is a core of a Bol loop, it is a core of a Bol loop of order 4, hence a core of an abelian group, a contradiction.
- Cores of abelian groups are medial

