
Poincaré–Steklov operator
Encyclopedia
In mathematics
, a Poincaré–Steklov operator (after Henri Poincaré
and Vladimir Steklov
) maps the values of one boundary condition of the solution of an elliptic partial differential equation in a domain to the values of another boundary condition. Usually, either of the boundary conditions determines the solution. Thus, a Poincaré–Steklov operator encapsulates the boundary response of the system modelled by the partial differential equation. When the partial differential equation is discretized, for example by finite elements or finite differences, the discretization of the Poincaré–Steklov operator is the Schur complement
obtained by eliminating all degrees of freedom inside the domain.
Note that there may be many suitable different boundary conditions for a given partial differential equation and the direction in which a Poincaré–Steklov operator maps the values of one into another is given only by a convention.
in a body for given temperature values on the body surface. Then the resulting heat flux
through the boundary (that is, the heat flux that would be required to maintain the
given surface temperature) is determined uniquely. The mapping of the surface temperature to the surface heat flux is a Poincaré–Steklov operator. This particular Poincaré–Steklov operator is called the Dirichlet to Neumann (DtN) operator. The values of the temperature on the surface is the Dirichlet boundary condition
of the Laplace equation, which describes the distribution of the temperature inside the body. The heat flux through the surface is the Neumann boundary condition
(proportional to the normal derivative of the temperature).
Mathematically, for a function harmonic
harmonic
in a domain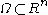 , the Dirichlet-to-Neumann operator maps the values of
, the Dirichlet-to-Neumann operator maps the values of  on the boundary of
on the boundary of 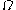 to the normal derivative
to the normal derivative 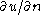 on the boundary of
on the boundary of 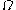 . This Poincaré–Steklov operator is at the foundation of iterative substructuring.
. This Poincaré–Steklov operator is at the foundation of iterative substructuring.
in the exterior of the sphere. Approximations of this operator are at the foundation of a class of method for the modeling of acoustic scattering in infinite medium, with the scatterer enclosed in the sphere and the Poincaré–Steklov operator serving as a non-reflective (or absorbing) boundary condition.
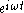 ) tangential electric field on the boundary of a conductive body to the electric current through the boundary.
) tangential electric field on the boundary of a conductive body to the electric current through the boundary.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Poincaré–Steklov operator (after Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
and Vladimir Steklov
Vladimir Steklov
Vladimir Andreevich Steklov was a Soviet/Russian mathematician, mechanician and physicist.Steklov was born in Nizhny Novgorod, Russia. In 1887, he graduated from the Kharkov University, where he was a student of Aleksandr Lyapunov. In 1889–1906 he worked at the Department of Mechanics of this...
) maps the values of one boundary condition of the solution of an elliptic partial differential equation in a domain to the values of another boundary condition. Usually, either of the boundary conditions determines the solution. Thus, a Poincaré–Steklov operator encapsulates the boundary response of the system modelled by the partial differential equation. When the partial differential equation is discretized, for example by finite elements or finite differences, the discretization of the Poincaré–Steklov operator is the Schur complement
Schur complement
In linear algebra and the theory of matrices,the Schur complement of a matrix block is defined as follows.Suppose A, B, C, D are respectivelyp×p, p×q, q×p...
obtained by eliminating all degrees of freedom inside the domain.
Note that there may be many suitable different boundary conditions for a given partial differential equation and the direction in which a Poincaré–Steklov operator maps the values of one into another is given only by a convention.
Dirichlet-to-Neumann operator on a bounded domain
Consider a steady-state distribution of temperatureTemperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
in a body for given temperature values on the body surface. Then the resulting heat flux
Heat flux
Heat flux or thermal flux is the rate of heat energy transfer through a given surface. The SI derived unit of heat rate is joule per second, or watt. Heat flux is the heat rate per unit area. In SI units, heat flux is measured in W/m2]. Heat rate is a scalar quantity, while heat flux is a vectorial...
through the boundary (that is, the heat flux that would be required to maintain the
given surface temperature) is determined uniquely. The mapping of the surface temperature to the surface heat flux is a Poincaré–Steklov operator. This particular Poincaré–Steklov operator is called the Dirichlet to Neumann (DtN) operator. The values of the temperature on the surface is the Dirichlet boundary condition
Dirichlet boundary condition
In mathematics, the Dirichlet boundary condition is a type of boundary condition, named after Johann Peter Gustav Lejeune Dirichlet who studied under Cauchy and succeeded Gauss at University of Göttingen. When imposed on an ordinary or a partial differential equation, it specifies the values a...
of the Laplace equation, which describes the distribution of the temperature inside the body. The heat flux through the surface is the Neumann boundary condition
Neumann boundary condition
In mathematics, the Neumann boundary condition is a type of boundary condition, named after Carl Neumann.When imposed on an ordinary or a partial differential equation, it specifies the values that the derivative of a solution is to take on the boundary of the domain.* For an ordinary...
(proportional to the normal derivative of the temperature).
Mathematically, for a function
 harmonic
harmonicHarmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
in a domain
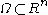 , the Dirichlet-to-Neumann operator maps the values of
, the Dirichlet-to-Neumann operator maps the values of  on the boundary of
on the boundary of 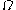 to the normal derivative
to the normal derivative 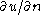 on the boundary of
on the boundary of 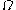 . This Poincaré–Steklov operator is at the foundation of iterative substructuring.
. This Poincaré–Steklov operator is at the foundation of iterative substructuring.Dirichlet-to-Neumann operator for a boundary condition at infinity
The solution of partial differential equation in an external domain gives rise to a Poincaré–Steklov operator that brings the boundary condition from infinity to the boundary. One example is the Dirichlet-to-Neumann operator that maps the given temperature on the boundary of a cavity in infinite medium with zero temperature at infinity to the heat flux on the cavity boundary. Similarly, one can define the Dirichlet-to-Neumann operator on the boundary of a sphere for the solution for the Helmholtz equationHelmholtz equation
The Helmholtz equation, named for Hermann von Helmholtz, is the elliptic partial differential equation\nabla^2 A + k^2 A = 0where ∇2 is the Laplacian, k is the wavenumber, and A is the amplitude.-Motivation and uses:...
in the exterior of the sphere. Approximations of this operator are at the foundation of a class of method for the modeling of acoustic scattering in infinite medium, with the scatterer enclosed in the sphere and the Poincaré–Steklov operator serving as a non-reflective (or absorbing) boundary condition.
Poincaré–Steklov operator in electromagnetics
Here, the Poincaré–Steklov operator is defined to be the operator mapping the time-harmonic (that is, dependent on time as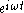 ) tangential electric field on the boundary of a conductive body to the electric current through the boundary.
) tangential electric field on the boundary of a conductive body to the electric current through the boundary.See also
- Fluid-structure interactionFluid-Structure InteractionFluid-structure interaction is the interaction of some movable or deformable structure with an internal or surrounding fluid flow. Fluid-structure interactions can be stable or oscillatory...
(boundary/interface) analysis - Schur complement domain decomposition methodSchur complement methodIn numerical analysis, the Schur complement method, named after Issai Schur, is the basic and the earliest version of non-overlapping domain decomposition method, also called iterative substructuring. A finite element problem is split into non-overlapping subdomains, and the unknowns in the...

