Perron method
Encyclopedia
In the mathematical study of harmonic functions, the Perron method, also known as the method of subharmonic function
s, is a technique introduced by Oskar Perron
for the solution of the Dirichlet problem
for Laplace's equation
. The Perron method works by finding the largest subharmonic function with boundary values below the desired values; the "Perron solution" coincides with the actual solution of the Dirichlet problem if the problem is soluble.
The Dirichlet problem is to find a harmonic function in a domain, with boundary conditions given by a continuous function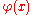
. The Perron solution is defined by taking the pointwise supremum over a family of functions 
,
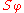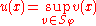
where
is the set of all subharmonic functions such that 
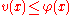on the boundary of the domain.
The Perron solution u(x) is always harmonic; however, the values it takes on the boundary may not be the same as the desired boundary values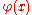
. A point y of the boundary satisfies a barrier condition if there exists a superharmonic function 
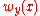, defined on the entire domain, such that 
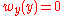and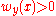 
for all 
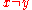. Points satisfying the barrier condition are called regular points of the boundary for the Laplacian. These are precisely the points at which one is guaranteed to obtain the desired boundary values: as 
.
The characterization of regular points on surfaces is part of potential theory
. Regular points on the boundary of a domain
are those points that satisfy the Wiener criterion: for any 
, let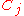 
be the capacity
of the set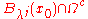
; then 
is a regular point if and only if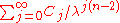
diverges.
The Wiener criterion was first devised by Norbert Wiener
; it was extended by Werner Püschel to uniformly elliptic
divergence-form equations with smooth coefficients, and thence to uniformly elliptic divergence form equations with bounded measureable coefficients by Walter Littman, Guido Stampacchia
, and Hans Weinberger
.
| issn=0025-5874 | volume=34 | issue=1 | pages=535–553}}
Subharmonic function
In mathematics, subharmonic and superharmonic functions are important classes of functions used extensively in partial differential equations, complex analysis and potential theory....
s, is a technique introduced by Oskar Perron
Oskar Perron
Oskar Perron was a German mathematician.He was a professor at the University of Heidelberg from 1914 to 1922 and at the University of Munich from 1922 to 1951...
for the solution of the Dirichlet problem
Dirichlet problem
In mathematics, a Dirichlet problem is the problem of finding a function which solves a specified partial differential equation in the interior of a given region that takes prescribed values on the boundary of the region....
for Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
. The Perron method works by finding the largest subharmonic function with boundary values below the desired values; the "Perron solution" coincides with the actual solution of the Dirichlet problem if the problem is soluble.
The Dirichlet problem is to find a harmonic function in a domain, with boundary conditions given by a continuous function
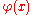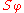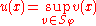
. The Perron solution is defined by taking the pointwise supremum over a family of functions ,where
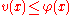is the set of all subharmonic functions such that on the boundary of the domain.The Perron solution u(x) is always harmonic; however, the values it takes on the boundary may not be the same as the desired boundary values
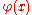. A point y of the boundary satisfies a barrier condition if there exists a superharmonic function 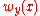, defined on the entire domain, such that 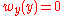and 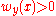for all 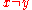. Points satisfying the barrier condition are called regular points of the boundary for the Laplacian. These are precisely the points at which one is guaranteed to obtain the desired boundary values: as .The characterization of regular points on surfaces is part of potential theory
Potential theory
In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
. Regular points on the boundary of a domain
are those points that satisfy the Wiener criterion: for any , let 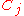be the capacityCapacity of a set
In mathematics, the capacity of a set in Euclidean space is a measure of that set's "size". Unlike, say, Lebesgue measure, which measures a set's volume or physical extent, capacity is a mathematical analogue of a set's ability to hold electrical charge. More precisely, it is the capacitance of...
of the set
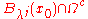; then is a regular point if and only if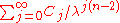diverges.
The Wiener criterion was first devised by Norbert Wiener
Norbert Wiener
Norbert Wiener was an American mathematician.A famous child prodigy, Wiener later became an early researcher in stochastic and noise processes, contributing work relevant to electronic engineering, electronic communication, and control systems.Wiener is regarded as the originator of cybernetics, a...
; it was extended by Werner Püschel to uniformly elliptic
Elliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
divergence-form equations with smooth coefficients, and thence to uniformly elliptic divergence form equations with bounded measureable coefficients by Walter Littman, Guido Stampacchia
Guido Stampacchia
Guido Stampacchia was a 20th century mathematician.Stampacchia was born in Naples, Italy. He obtained his high school certification from the Liceo-Ginnasio Giambattista Vico in Naples in classical subjects, although he showed stronger aptitude for mathematics and physics.In 1940 he was admitted to...
, and Hans Weinberger
Hans Weinberger
Hans F. Weinberger is an Austrian-American mathematician, known for his contributionsto partial differential equations and fluid dynamics....
.
Further reading
| year=1972}} | year=1932 | journal=Mathematische ZeitschriftMathematische Zeitschrift
Mathematische Zeitschrift is a mathematical journal for pure and applied mathematics published by Springer Verlag....
| issn=0025-5874 | volume=34 | issue=1 | pages=535–553}}